Introduction
Glacier dynamics could not be approached without making local fluctuations disappear to a greater or lesser extent by smoothing. In doing this we can suppress fluctuations having a wavelength less than some few times the glacier thickness. This overall view (Reference LliboutryLliboutry, 1968) allows us to study the mass balance and kinematic waves, but not, for example, an ice fall, the extreme end of a glacier, or crevasse systems.
It is this detailed point of view that we shall consider in this paper. We will only eliminate details with a scale of some ten metres or less. An ice fall seems to a man to be an impassible chaos of seracs, but these irregularities only concern a relatively thin surface layer. Whether on the surface we have seracs separated by very wide crevasses or a uniform layer of ice of the same weight, at a depth of some tens of metres the stresses and strains are the same (by extending to plasticity St Venant’s principle as used in elasticity).
We shall seek to approximate the stresses and strains in a limited region of a glacier by polynomials in x, y and z. Then we shall apply the formulae obtained to a specific case where, for a distance of about a kilometre, velocities, curvature, thickness etc. vary considerably.
Flow Law of Ice
We shall assume as usual: (a) that only the stress and strain-rate tensors enter, and not terms introduced by the mechanics of finite deformation; (b) that the relation between these tensors is linear; (c) that the ice is incompressible and isotropic; (cl) it follows from these three hypotheses (Reference Lliboutry and ChowLliboutry, in press) that at a given point the strain-rate tensor
(we shall write σ′ ij as simply σ′ i when i = j, and as τ ij when i≠j).
As usual we shall assume that the “viscosity” η is a function only of the second invariant of one or other of the tensors. This invariant can be replaced by the effective shear stress, which for the plane problem reduces to
One can adopt the general law of Reference GlenGlen (1955)
but the sector of values proposed for n and B is large.
In laboratory experiments, when transient creep has not been fully eliminated (and this seems to be the case for Reference SteinemannSteinemann’s (1958) measurements), one finds that n increases with τ. For low values of τ, n tends to 1. The values found by Glen before he eliminated transient creep, and which he represents by the following law (bearing in mind that he uses σ = τ√3 and
are much better represented by the following law, which allows us to express
as is shown in Table I.
Table I Comparison of Flow Laws with the “Minimum Strain-Rates” Found by Glen

Glen modified his laboratory measurements in attempting to eliminate the part played by transient creep. For polycrystalline temperate ice, he obtained in this way five values which gave him (in metre-bar-year units) n = 4.2, B = 0.296. However the law adopted for transient creep is open to question, and further for glacier ice the law is perhaps different. The results collected together by Reference MeierMeier (1960), who brought together these corrected values of Glen’s and others obtained on glaciers at low
The exponent 4.5 was chosen according to Weertman’s theory, since abandoned. Those of the results obtained taking account of the longitudinal strain-rate are equally well represented by the law:
the coefficients of which have been estimated graphically plotting
It thus seems that at the present state of our knowledge we can adopt a flow law

This has the very great advantage as compared with Glen’s law then it can lead to analytic solutions for stresses and strains even if they cancel at the origin. But it must be realized that the law does differ basically from the law of Equation (3), and that the study of temperate glaciers will allow us some day to decide between the two. If three pairs of variables (
It is therefore of interest for glaciologists to use Equation (8) as a flow law to analyse their results. To evaluate B 0, B 1 and B 2, it is only necessary to plot
General Equations for the Plane Problem when the Surface is Flat
We shall consider compressions positive, which results in some modifications of the classical formulae.
Let us consider a small volume of a continuous medium. We consider the normal to the surface towards the interior, and choose as positive sense for stresses those indicated in Figure 1 (a and b). Let us consider a surface whose normal makes an angle θ with Ox. The medium outside exerts on this little volume a stress whose components are (cf. Fig. 1c):

parallel to an axis obtained by rotating


Fig. 1. Notation and sign convention for the plane problem.
When the glacier surface is flat, it is convenient to take the following as cartesian coordinates (Fig. 2): Ox along the line of greatest slope, Oz normal to the surface downwards. If we put u and w for the components of velocity parallel to Ox and Oz, the fact that the coordinates are cartesian implies that


Fig. 2. Cartesian axes adopted for the plane problem.
We shall limit ourselves to begin with to the plane problem (flow lines in vertical planes parallel to y = constant). Thus:

The equilibrium conditions reduce to:

With the axes chosen in this way, α is the (positive) angle that Ox makes with the horizontal, and for z = 0, the boundary conditions are:
Approximate Solutions Near the Origin
Near the origin, the components of velocity, u and w, can be approximated by polynomials in x and z. To satisfy Equations (14) and (16), these velocities must have the form

O 3 stands for terms in x and z of third or higher order (not the same in each case). All the coefficients u 0, a, c, …, with the exception of k can be determined from the velocities of stakes fixed in the glacier surface, their velocity components being

We see that it is just as important to determine movements perpendicular to the surface as parallel to it, and that simple measurements between stakes, such as those proposed by Nye (1959), without observations from fixed stations off the glacier, are insufficient.
According to Equation (12), the strain-rates are

The second-order terms in the strain-rates can not be determined in practice because one would have to be able to determine third-order terms in the velocities, and above all because of the existence of correction terms of which we shall speak later (when the problem is not plane and the surface curves). We cannot therefore expect in practice to get anything beyond first-order terms for the stresses. Nothing however stops us from examining the form which second-order terms should have; the method indicated below allows this.
We can easily show that, to satisfy Equations (15) and the boundary conditions, Equations (16), if the origin is not a singularity, the development around the origin must have the form

The stress deviator σ′ z = −σ′ x takes the simple form
The Lévy–Mises equations (1) can be written, if one uses as flow law Equation (8),

It only remains to substitute for
When only looking for the leading terms, one can proceed much more quickly by writing the Lévy–Mises equations, whatever the flow law adopted,

At the origin itself

Compared with this state, strain-rates and stresses near the origin have undergone a perturbation. The ratio of the perturbations is in this case equal to the differential viscosity

If one adopts flow law (8), then

Starting from measured values of a, one first determines A from
from which we get

If one retains Glen’s law as flow law (Equation (3)), then Equations (26) and (27) have to be replaced by

In this case the calculation is somewhat faster, but the terminated expansion in 1/n is only valid if a ≫ 2mx+2ez. When a = 0 it is necessary in order to obtain a terminated expansion, to take the origin at a certain depth below the surface.
The above approximate formulae allow us to study the stresses from the detailed point of view, for which Reference NyeNye’s (1957) classical solution is no longer valid. We recall that this solution presupposes stresses and strains independent of x (c = m = e = 0, M = E = 0).
Reference Paterson and SavagePaterson and Savage (1963[a], Reference Paterson and Savage[b]; Reference Savage and PatersonSavage and Paterson, 1963) have already introduced terms in c and e, but not the one in m. The present author (Reference LliboutryLliboutry, 1964–65, Tom. 2, p. 592–94) has already introduced terms in m and c, but in a case limited to a Newtonian viscosity (B 1 = B 2 = 0) and for a constant thickness h, which has as consequence that e = 0 and m = −c/2h. For a Newtonian viscous body and the plane problem, a general solution has recently been given by Reference Shumskiy and ŌuraShumskiy (1967) (but this solution is only rigorous for the case of a flat glacier surface, contrary to what the author seems to believe).
Application to the Study of Friction
Let us suppose that the first-order expressions found for the stresses, and those of the second order for the velocities, constitute valid approximations right down to the rock bed. This must be the case for a thin layer of ice sliding rapidly. If the thickness h of the ice layer is known at x = 0, one can estimate the slope β of the bedrock, and then calculate the sliding velocity U and the friction per unit area f with the aid of the following relations (the suffix h indicates values at depth h):
This last equation, already given by Reference LliboutryLliboutry (1968), can be deduced from Equation (11) putting T = −f and
Even if the thickness is uniform (α = β), the friction is not equal, from the detailed point of view, to ρgh sin α. It is
(a differential equation giving f has also been given by Reference Shumskiy and OdishawShumskiy and others, [c1964], but as it presupposes Newtonian viscosity and does not take account of terms introduced by the curvature of the surface, it is not rigorous, and so of little interest).
Study of a Simple Example
To illuminate this possibility (f ≠ ρgh sin α), we shall now examine a simple example which is somewhat like the cirque glaciers studied by Reference LewisLewis and others (Lewis, 1960) if, as we shall suppose, the ice can be approximated by a Newtonian viscous body (B 1 = B 2 = 0). We recall that for the plane problem and a Newtonian viscous body, a very general solution has been given by Reference Shumskiy and ŌuraShumskiy (1967).
Let us suppose that in Equations (17) the O 3 terms are zero, and that, with u 0, D and R positive constants

(we have arbitrarily put e = 0 and k = −2m in order to obtain a simple geometrical solution). We take our origin at the equilibrium line. If the glacier is in a state where the mass balance b = w 0 at the surface, Z being the altitude,

Furthermore, Equations (23) and (24) give, when

whence
sin α and ∂b/∂Z being determined by the location, it follows that u 0/R 2 and D are determined by the location. The expressions for the velocities are then

We see that at the centre of the glacier the velocities initially increase with depth. The flow lines have as equations

Φ is a constant which represents the volume flux per unit width passing between the point under consideration and the equilibrium line x = z = 0. A flow line joins the points (−L, 0) and (+L, 0) going through the point (0, h) where

When Φ = u 0 D the flow line consists of the line parallel to the surface z = D and the two arcs of the circle x 2+z 2 = R 2, as shown in Figure 3. Other flow lines are also shown there. One can trace them out point by point by writing Equation (36) in the form


Fig. 3. Simple example where f ≠ ρgh sin α. The dashed part is without physical significance in the case of a glacier.
Any one of these flow lines could constitute the rock bed provided two conditions are simultaneously satisfied:
(a) The law of friction must be satisfied: taking account of Equations (23), (25) and (35),
Equations (16) and (17) for the stresses then become

At the centre, we have the shear stress on the bed as

With other flow lines as lower limit of the glacier, the friction no longer tends to zero at its two extremities for sin 2(α−β) does not cancel out there. This however is not necessarily absurd, the friction can vary in the opposite sense from the velocity (Reference LliboutryLliboutry, 1968). One can therefore suppose that the roughness and drainage at the bedrock are such that the law of friction is everywhere satisfied.
On the other hand the flow lines shown dashed in Figure 3 which describe closed loops below z = D can have no physical significance, since the frictional force is in the direction of movement. (In a general way, it does not seem likely that “eddies” of ice cut off from all accumulation could exist in hollows of the bedrock, however deep they might be.)
(b) The stress perpendicular to the bedrock must be a compression, the wall not being able to exercise a pull on a temperate glacier. The most critical point is the upper limit of the glacier (x = −L, z = 0). As atmospheric pressure can make itself felt between the ice and rock, it does not enter. σ xy is always negative, σ z is zero, which leads to the condition |β−α| ≤ 45°, or u > w. Using Equation (39) this can be written
or
This condition is not necessary when the glacier is limited at the top not by rock, but by an ice cap.
General Equations in Curvilinear Coordinates
It is rare that the surface of a glacier, even smoothed so as to make all the sinuosities of wavelength less than the thickness disappear, can be approximated by a plane. Let us consider the much more general case where this is not so, the contours of the surface nevertheless remaining parallel straight lines.
It is then advantageous, if we wish to obtain approximate analytical solutions, to use curvilinear coordinates. The x-axis will be a line of greatest slope. The curves x = constant will be perpendiculars to this line. The abscissa x of a point is the distance measured along the surface, its ordinate z is the distance from the surface. (It must be assumed that the centre of curvature of the surface is never found within the glacier.) The conditions at the upper surface then remain the simple conditions (16).
With these curvilinear axes, Equations (12) and (15) cease to be valid:
(a) The true distance between two points having the same z and abscissae x and x+dx is not dx but

where R is the radius of curvature counted positive when the surface is convex. In Equations (12) and (15), derivatives with respect to x must be multiplied by dx/dx 0 = R/(R−z).
(b) To write the equilibrium conditions, we must consider the little parallelopiped of dimensions dx, dy, dz. The two faces separated by dz are tangents to surfaces z = constant (Fig. 4). The others differ by an angle dx 0/(R−z). The stresses acting on this face are no longer X and Z given by Equations (9), but N and T given by Equations (10) and (11), with



Fig. 4. Diagram to illustrate the equilibrium equation with curvilinear coordinates.
Further, on this face the tangential force parallel to Oy is not simply



or finally

Analogous correction terms enter into the strains as examination of Figure 5 shows. Their Equations (12) must be replaced by


Fig. 5. Diagram to illustrate the calculation of strain-rates in curvilinear coordinates.
The σ ij and the
Calculation of the Deformations Around the Origin in the General Case
A good photogrammetric survey of the surface allows the determination of the slope α(x), and thence of the curvature 1/R = dα/dx and even, with rather low precision, the variation of this curvature d2 α/dx 2. It is illusive to wish to go further. We shall therefore put

which implies

Furthermore, in general, the width of the ice stream varies, and the problem ceases to be plane. We nevertheless assume the valley to be rectilinear and thus the plane y = 0 to be a symmetry plane for the flow (at least to the third-order terms in x, y and z). v being the component of velocity in the transverse direction Oy, its expansion is an odd function of y, while for u and w it is an even function. We shall put

assuming that terms in yz do not exist. (This amounts to assuming that flow lines starting from points with the same x and y have an identical projection on the glacier surface at least to terms of third order.) With this hypothesis, one can determine Λ and Λ′ graphically. If ϒ is the width of an ice stream, its variation along Ox is

We retain for u and w the Equations (17), with supplementary terms in y 2. The expansions of the velocities can then be written

And taking account of Equation (56)
Equations (49) then give the strain-rates



It can be seen that s′ can be determined from measurements of the displacement of stakes, at least in theory. If we have been able to find such a relation determining s′, it is because we have imposed the limitation that lines of greatest slope shall be parallel to Ox.
With Equations (61), the shear strain-rates parallel to the surface are reduced to

Until now we have only had an estimate due to Reference NyeNye (1959), made under the assumption that w 0 = e = c = m = Λ = 0. The
Nye supposes that, when the sliding is rapid (u 0 = u b),
He then applies his classical solution to calculate the stresses, although it is not valid except for a uniform layer of ice. However, the thickness ceases to be uniform as soon as the surface is curved. The actual calculation of the stresses is more subtle, and involves Γ.
Calculation of the Stresses in the General Case
The method used to calculate the stresses for the plane problem and a flat surface can be extended to cover the general case. We shall confine ourselves to finding the first-order terms.
The symmetry of the flow with respect to the plane y = 0, and Equations (59) and (60) for the strain-rate components to which the stress deviator components are proportional, show that σ x , σ y , σ z , and τ xz must be even functions of y, while τ xy and τ xz must be odd functions. We shall therefore put a priori, so as also to satisfy the boundary conditions for z = 0,

The equilibrium conditions, Equations (52), give that

The Lévy-Mises equations can be written

(there is no need to add the ratio
At the origin itself these equations give

For small deviations starting from this state, it is the differential viscosity which enters. A variation of x gives

a variation of z

From Equations (68) and (69) we deduce that

To simplify this, we shall define n by the equation
even if we are not adopting Glen’s flow law.
M and S being known, we deduce k from Equation (68)

Finally, from Equation (70) we deduce E and E′. These calculations give

For the calculation of the friction we need

To calculate
At the origin the effective strain-rate is
If we adopt the flow law given by Equation (4),
We calculate τ 0, then
If we adopt Glen’s law, we would have directly

but we have to verify that a ≫ 2mx+2ez.
Application to a Particular Case
We have applied the above equations to the ice fall of the Mer de Glace (in the wide sense) between the place called “la Bédière” and the Glacier du Tacul. We have available a stereo-plot at 1 : 10000 made by the Institut Géographique National from their aerial coverage in 1958, measurements of surface velocity made between 13 April and 20 July 1960 (Lliboutry and others, 1962) and in the lower part several seismic reflection sites (Reference VallonVallon, 1961). Figure 6 shows a map of the area.

Fig. 6. Map of the region studied after the stereo-plot of the Institut Géographique National (aerial photography in 1958). Smoothed contour lines. Only the largest crevasses and the cliff of seracs are indicated. The arrows represent the displacement in 100 d. The ice stream studied is bounded by the dashed lines.
The first problem is to determine the central ice flow line. This is indicated by the medial moraines coming from la Noire and Petit Rognon, and by the septum called “la Bédière”, which marks the confluence of the Glacier du Géant with the Vallée Blanche, a septum the trace of which is found again immediately below the seracs and which we shall take as the western limit of the ice stream. We are also guided by the series of large transverse crevasses of the Glacier du Géant and by the shape of the contour lines. This ice stream is only rectilinear for about 800 m. On either side it curves, but, of the six points studied, only the two most down-glacier (e and f) are off the rectilinear portion.
A more troublesome fact is that, in the lower part, seismic soundings have shown that the rock bed deepens towards the right margin (east side), the thickness of the glacier (measured perpendicular to the slope) there reaches 390 m, whereas it is only some 280 m near the centre, and doubtless even less at the Ieft margin. This shows itself on the surface by the fact that the contour lines cease to be perpendicular to the ice flow, and that the maximum velocity is displaced towards the right margin.
Taking account of the whole mass balance of the glacier, the discharge of the central ice stream must be between 12 and 15 hm2/year. The observed thicknesses (if they are not the result of erroneous interpretation of the seismograms) lead to a discharge of at least 20 hm3/year. However, it seems that in this lower part the ice stream coming from the right side of the Glacier du Géant disappears from the surface; it plunges in the place indicated and the central ice stream superposes itself partially on top of it.
The conclusion is that the results found for points e and f will doubtless be only gross approximations.
Longitudinal profiles along the axis of flow and 100 m to either side of it are shown in Figure 7. They allow us to trace the mean surface, that is to say the x-axis, and to graduate it. We can then determine α(x) graphically, and its derivative (Γ+Γ′x). In order that Γ′ should not take very high values, some adjustments are made to these curves. In this way a certain amount of smoothing is done, necessarily somewhat subjectively. (This will be improved in proper calculations to be carried out later by a procedure which is more automatic and objective.) The determination of the width of the ice current ϒ and its logarithmic derivative (Λ+Λ′x) is easier. All these functions of x are plotted in Figure 8.

Fig. 7. Longitudinal cross-section. Three longitudinal profiles of the surface separated from each other by 100 m have been included. The curvilinear axes based on the mean profile are shown. (a): Bedrock estimated from a first analysis of the velocities (this paper), (b): Bedrock determined by seismic reflexion (Reference VallonVallon, 1961).

Fig. 8. Fig. 8. Determination of various parameters which appear in the study of the flow.
The determination of u(x), very high in this region, cannot be done to the precision we would wish for a fundamental reason, which is not entirely dissimilar from Heisenberg’s uncertainty principle in quantum physics. If one measures the displacement over a very short time, the location is perfectly determinate, but the velocity is perturbed by seasonal or random perturbations (related to the opening of crevasses, the toppling of seracs, the collapse of sub-glacial cavities). If one measures the displacement between two instants more separated in time, one has a good average velocity with time, but relative to a poorly defined location. Here again we must seek to make the derivative (a+2mx) as smooth as possible.
As for w(x) and its derivative (−c—2ex), we shall accept that these are practically equal to the balance, itself not known very precisely because the annual displacement is too large, and because it is not possible to place stakes in the region with seracs. This is however unimportant as the corresponding terms are negligible in the calculations.
It remains to determine s. It can be estimated starting from the fact that at the top of the ice fall the crevasses are straight and at the bottom ogives appear which are markedly arcuate. The centre has travelled a distance L, the margins a distance L−ΔL. Assuming that the ratio of the surface velocities along the axis of the stream and at the edges is independent of x,
In this way we find s = 1.72×10−6 u 0m−2 (u 0 in m/year).
The values of the velocity coefficients taking successively as origin each of the six points a, b, c,…, f marked on Figure 7, are presented in Table II. Apart from the last, these points have been chosen in such a way that either Γ or Γ′ is zero; this simplifies the calculations.
Table II. Initial Numerical Values

Calculation of the Velocities at Depth and Determination of the Rock Bed
The calculation of the effective variables has been carried out using Glen’s law and using the polynomial proposed in Equation (7). As Table III shows, the results are not very different. We shall here follow the calculations using Equation (7).
Table III Effective Variables at the Origin

The velocities at depth below the origin, bearing in mind that the terms in c and w 0 are negligible, are given by

with

These coefficients are given in Table IV, and the corresponding profiles in Figure 9.
Table IV Determination of the Velocities at Depth and of the Rock Bed


Fig. 9. Velocity profiles at various points of the ice fall, and most probable level of bedrock.
The velocity vectors being given in the longitudinal profile (Fig. 7), the line of the rock bed can be found with sufficient precision if we do not have the difficulties indicated above for the points e and f. A more exact calculation will be made when the surface velocities have been measured with more precision (a) in the ice fall by terrestrial photogrammetry from the region of the Requin hut, (b) near “la Bédière” with the help of accumulation stakes (square-sectioned steel tubes, anchored at their bases) whose position could be determined by intersection from fixed points. These measurements are now in progress.
Table IV also contains the thicknesses h thus found, and the corresponding values of the discharge ϕ, of u, w and (α−β). Between two points the variation in discharge must be equal to the sum of the balance over all surfaces of the ice stream. This allows us, if we suppose one value of h to be perfectly known, to determine the others with precision. In the present case h at the lower extremity has been measured by seismic reflexion and the values of b in this region by ablation stakes (Reference VallonVallon, 1961). The equilibrium line b = 0 can be located by visual inspection. We note that at the point e, where u h and w h become small, the calculation of α−β breaks down.
Calculation of the Stresses and Friction
To calculate the stresses, we must calculate at each point

These values are given in Table V, as are those of k given by Equation (73). 2A is the value of
Table V Calculation of the Stresses and Friction

Between a and d, the sliding velocity U decreases from 834 to 252 m/year, while the friction increases from 1.06 to 4.28 bar. For these high-sliding velocities, the friction appears to be largely proportional to the normal pressure N − H.
These provisional results, imprecise as they are, are manifestly contrary to Weertman’s theory according to which the friction varies in the same direction as the velocity, the pressure having no influence. They seem on the other hand to agree with my theory (Reference LliboutryLliboutry, 1968, Reference Lliboutry and Chowin press). For the “global” friction, in which the effect of large-scale undulations of the bedrock is included, we find a friction that is practically independent of the velocity and largely proportional to the pressure. But here it is the “detailed friction” which enters, in which one limits oneself to considering the effect of undulations of wavelength λ 2 (several metres), λ 3 (several decimetres), and λ 4 (several millimetres). One then finds a friction which varies in the opposite direction to the velocity, and always in the same direction as the normal pressure.
The roughness r which comes into the theory seems to have to be equal to 0.3 or more, contrary to what has been assumed up to now. The numerical calculations of my sliding theory ought to be repeated for large values of the roughness to allow a quantitative comparison.
The low value of the friction found at the point f despite a sliding velocity that is still high and a thickness also still high, probably arises because the ice stream studied has been partially superposed on another.
Conclusions
This numerical example has been presented more to indicate the procedure to be adopted than to arrive at definite results. In order to improve it, it is necessary (a) to take points separated from each other by a distance approximately equal to the thickness of the glacier at the point in question, (b) determine the thicknesses both above and below the ice fall by a good seismic survey.
One can also study zones which are less rapid, and where the thickness has been able to be determined directly in other ways. However, it would then be necessary to approximate to the velocities and stresses by polynomials of higher order.
In this way we may hope to obtain rapidly numerous simultaneous values of f, N and U, and to determine experimentally in an irrefutable way the law of friction of temperate glaciers.
Appendix
Incompatibility of a Law  with GLEN’S LAW
with GLEN’S LAW 
Let us suppose that a law of Glen’s form, with n between 3 and 5, suitably represents three pairs of values
The proof of this depends on the fact that the determinant

with 0 < α < β < γ and m > 1 is positive. It can be written as

In the extreme right-hand side, the quantities in parentheses are all positive. As m > 1, the curve y = x m s concave upwards. and

It follows that δ > 0.
Now let us write down the equations which determine B 0, B 1 and B 2

From this we deduce that

where

Hence

Since we have assumed 3<n < 5, 2/(n−3)>1, 4/(n−1) > 1 and (n−1)/2 > 1. So, by virtue of the theorem proved above, these three last determinants are positive, and thus
One can treat in a similar manner the case when n is outside the interval from 3 to 5. A simple heuristic argument is as follows:
For n = 3, B 0 = B 2 = 0. Thus when n passes through the value 3, B 0 and B 2 change sign. Thus for 1 < n < 3
For n = 5, B 0 = B 1 = 0. Thus for n > 5


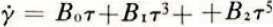 . We initially consider a plane problem with a flat glacier surface. In a simple example the theoretical possibility of very important deviations from the classical relation
. We initially consider a plane problem with a flat glacier surface. In a simple example the theoretical possibility of very important deviations from the classical relation 













