Introduction
Several authors have treated the relationship between glacier surface and bedrock topographies. Reference NyeNye (1959) calculated a first approximation using Glen′s flow law in a simple way. As more and better data on surface and base profiles became available, perturbation models were developed to explain the small-scale undulations caused by an irregular base. Reference BuddBudd (1970) described a perturbation method for Newtonian viscous media, and Reference Hutter, Hutter, Legerer and SpringHutter and others (1981) gave a systematic analysis of the governing equations and boundary conditions for first-order perturbation models.
Simplified perturbation models have been applied to several flow lines in areas with known surface and bedrock profiles. Reference Whillans and JohnsenWhillans and Johnsen (1983) used a linear viscous flow law to model the Byrd Station, West Antarctica, flow line, Reference Johnsen, Johnsen, Rasmussen and ReehJohnsen and others (1979) and Reference RasmussenRasmussen (unpublished) introduced a multi-layer model with Newtonian viscous flow, which was used by Reference Overgaard and RasmussenOvergaard and Rasmussen (1979) on the EGIG line, south Greenland. Reference Reeh, Reeh, Johnsen, Dahl-Jensen, Langway, Langway, Oeschger and DansgaardReeh and others (in press) modelled the flow-line up-stream from Dye 3, south Greenland, using Glen′s flow law with a flow-law parameter which varies exponentially with depth to account for changes in stress, temperature, ice fabrics, etc. The predicted Dye 3 surface undulations were 50% smaller than observed.
In this work, a more realistic flow-law parameter profile along the 2037 m deep bore hole at Dye 3 will be derived from Reference Gundestrup and HansenGundestrup and Hansens (1984) measurements of the temporal changes of the hole geometry. It will be used in a first-order, multi-layer, two-dimensional perturbation model, and the predicted surface undulations and strain-rates will be compared with observed data (Reference Overgaard, Gundestrup, Langway, Langway, Oeschger and DansgaardOvergaard and Gundestrup, in press; Reference Whillans, Whillans, Jezek, Drew and GundestrupWhillans and others, 1984).
Topography and Bore-Hole-Tilting Data
The Dye 3 bore hole is located at long. 65.19°N., lat. 43.82°W., 41.51 km east of the ice divide (Reference Overgaard, Gundestrup, Langway, Langway, Oeschger and DansgaardOvergaard and Gundestrup, in press). The base and surface elevations are known (Reference Overgaard, Gundestrup, Langway, Langway, Oeschger and DansgaardOvergaard and Gundestrup, in press) along three parallel lines (A, B, and C) as shown on Figure 1. Based on surface strain-rates (Reference Whillans, Whillans, Jezek, Drew and GundestrupWhillans and others, 1984) and repeated satellite fixed points (Reference Zwally, Zwally, Bindschadler, Brenner, Martin and ThomasZwally and others, 1983) the flow line (dotted line on Fig. 1) is estimated. Between 14B and −7B it is close to the B-line. In Figure 2 the surface and base elevations are shown along the A, B, and C lines. Obviously, the bedrock topography has undulations of up to 15% of the ice thickness. The dashed lines in Figure 2 are trend lines; the base trends are determined as the least-square linear fit to the observed base-elevation profiles, the surface trends as a least-square fit to an ice-sheet profile suggested by Reference NyeNye (1959). The dashed lines in Figure 2 represent the lower and upper boundaries to the basic flow in the perturbation modelling below.

Fig. 1. Surface elevation map of the Dye 3 region (Reference Overgaard, Gundestrup, Langway, Langway, Oeschger and DansgaardOvergaard and Gundestrup, in press), elevations in metres above sea-level. The Dye 3 drill hole is located at point lB. Basal and surface elevation profiles are measured along the three parallel lines A, B, and C. The filled circles mark the ends of the line intervals used in the model.

Fig. 2. Surface and basal elevation profiles along the A, B, and C lines. The full curves are observed and the dashed curves are trends of the profiles. The x-axis shows the distance in kilometres from the interception between the ice crest and the A, B, and C lines respectively. Dye 3 is located at 415 km on the B-line.
The inclination and azimuth profiles measured by logging of the Dye 3 deep hole in 1981 and 1983 (Reference Gundestrup and HansenGundestrup and Hansen, 1984) give information about the deformation rates of the ice. The horizontal velocity u(z) along the core (where z is the distance above the base) and its vertical gradient ∂u(z)/∂z were calculated with the assumption of laminar flow (Reference Gundestrup and HansenGundestrup and Hansen, 1984).
250 m above bedrock ∂u/∂z profile shows a sharp transition to much higher deformation rates at greater depths (Fig. 3a). This remarkable shift coincides with the transition between Holocene and Pleistocene ice (Reference Dansgaard and DansgaardDansgaard and others, 1982). The very highest deformation rates are found in the bottom 25 m of silty ice. In the upper 1000 m the inclination changes are too small to allow accurate estimates of ∂u(z)/∂z, but they do show that practically all of the deformation takes place at great depths, and that the flow of the Holocene ice at Dye 3 is essentially block flow.

Fig. 3. Flow-law parameters derived from the Dye 3 bore-hole-tilting measurements.
-
(a) The full curve shows ∂u/∂z for the bottom 700 m, points are the 50 m averaged ∂u/∂z values and the dashed curve represents values calculated from the model.
-
(b) The flow-law parameter estimated by Equation (2) for the bottom 700 m is shown as the full curve. The dashed curve is the best fit to the Arrhenius Equation (3). The B-profile used in the model is the full curve for z ⩽ 250 m and the dashed curve for z > 250 m.
-
(c) The enhancement factor E. The enhancement factor is the factor of the flow-law parameter B which depends on the impurity concentration, size, etc., in the ice. The enhancement factor does not depend on the ice temperature.
The Flow-Law Parameter
In order to simplify the calculation of the flow-law parameter, the flow is assumed to be two-dimensional and stationary, and Glen′s flow law for isotropic ice (Reference GlenGlen, 1955) is assumed to be valid. If the flow-law exponent is 3, as most results from bore-hole tilting suggest (Reference PatersonPaterson, 1981, Reference Paterson1983), the equation for shear deformation is:

u and w being the horizontal and vertical velocities, B the flow-law parameter, σ x , σ z , τ xz the stress components, x the axis parallel to the basal trend line, and z the axis perpendicular to the x-axis.
Near the bottom of the bore hole the deformation is dominated by shear, which allows the following approximation to Equation (1):

The flow-law parameter B is considered to be a function of temperature, ice fabric, ice crystal size, and impurity concentration in the ice.
The shear stress T xz is calculated as
ρ being the ice density, g the gravitational acceleration, α0 the mean surface slope at Dye 3 (averaged over 10 km (5H0)), and H0 the mean ice thickness at Dye 3 (averaged over 10 km (5H0)).
Perturbation models (Reference Reeh, Reeh, Johnsen, Dahl-Jensen, Langway, Langway, Oeschger and DansgaardReeh and others, in press) indicate that the simple linear Equation (3) gives a satisfactory description of the shear stress at the deep hole, in spite of the mountainous bedrock topography in the area.
The estimate of ∂u(z)/∂z from the bore-hole tilting and the calculated shear stress Txz from Equation (3) allow calculation of B for the bottom 700 m. The full curve in Figure 3b shows the calculated B-profile. At the Holocene to Pleistocene transition (z = 250 m), B increases by a factor of three, in agreement with the experiments of Reference Shoji, Langway, Langway, Langway, Oeschger and DansgaardShoji and Langway (in press), and in the 25 m of silty ice close to the base, B reaches a level approximately seven times higher than the Holocene value, which is 1.0 × 10−17 Pa−3 year−1, in agreement with the flow-law parameter suggested by Reference PatersonPaterson (1981). In the Holocene ice, B decreases slowly upwards. These trends will be interpreted below.
As to the Holocene ice, the decreasing temperature upward in the bore hole (Reference Gundestrup and HansenGundestrup and Hansen, 1984), essentially explains the variation of B, as can be verified by applying the Arrhenius equation in the interval 250 m z ⩽ 700 m:

Q being the activation energy (60 kJ/mol) (Reference PatersonPaterson, 1981), R the gas constant (8.314 J mol−1 K−1), and T the absolute temperature. The constant A0 is calculated to be 9.8 × 10−6 Pa−3 year−1 by inserting the measured B and T profiles through the said interval.
In order to explain the Pleistocene B-profile, it is practical to divide B into a temperature-dependent factor A(T) and an enhancement factor E that depends on other ice parameters.
According to Equation (4), E equals unity for 250 m < z ⩽ 700 m, and this is assumed to hold in all of the Holocene ice (z > 250 m). In the Pleistocene ice (0 < z ⩽ 250 m), E is calculated using Equation (5) and shown on Figure 3c. This part of the B-profile is probably to be explained by varying impurity concentration, crystal size, and ice fabric.
The measurements of ice-crystal size (Reference Herron, Herron, Langway, Brugger, Langway, Langway, Oeschger and DansgaardHerron and others, in press), dust concentration, and pH (Reference Hammer, Hammer, Clausen, Dansgaard, Neftel, Kristinsdottir, Johnsen, Langway, Langway, Oeschger, Dansgaard and WashingtonHammer and others, in press) along the deep ice core all give profiles characterized by nearly constant values in the Holocene ice, and different and highly variable values in the Pleistocene ice. The crystal size decreases by a factor of two at the Holocene to Pleistocene transition; the dust concentration increases by one to two orders of magnitude, and the ice becomes alkaline. The shape of the dust concentration profile is very similar to that of the deformation rate ∂u/∂Z profile (Reference Gundestrup and HansenGundestrup and Hansen, 1984).
The single-maximum c-axis fabric of the ice crystals intensifies with increasing depth (Reference Herron, Herron, Langway, Brugger, Langway, Langway, Oeschger and DansgaardHerron and others, in press), but it does not change drastically at the said transition to judge from the few measurements available in Pleistocene ice. Hence, the high deformation rates in Pleistocene ice cannot be explained by a c-axis alignment. This is why Reference Gundestrup and HansenGundestrup and Hansen (1984) concluded that dust concentration, and possibly other parameters that vary in a similar way, are responsible for the easy flow in Pleistocene ice. It should be mentioned that the enhancement factor defined by Equation (5) agrees with the observed variations of dust, etc., over the entire ice-sheet thickness.
In the perturbation model to be designed below, we also need the longitudinal strain rate ∂u/∂x(z), which is given by Glen′s flow law (Reference GlenGlen, 1955):

Glen′s flow law (Equation (1) and (6)) describes the deformation rates of istotropic ice. As the enhancement factor E is assumed to depend on parameters which hardly affect the isotropic properties of the ice. Glen′s flow law remains valid and the flow-law parameter B in Equation (6) is given by Equation (5).
Observations of the mean-diameter profile in the Dye 3 bore hole (Reference Gundestrup and HansenGundestrup and Hansen, 1984) support these considerations: the slowly increasing diameter with depth is caused by overpressure in the hole fluid since the hole was drilled, but the big diameter increase at the Holocene/Pleistocene ice are features similar to the observed variations of the ∂u/∂z and dust-concentration profiles. These diameter changes in the Pleistocene ice must result from higher and variable values of the flow-law parameter in Equation (6), resulting in a B-profile here similar to the B-profile in Equation (5).
The enhancement factor E is therefore used to model the softer ice, deposited during the last glaciation, and E is not used to model anisotropic ice.
As a final test on the derived flow-law parameter B (Equation (5)), the ∂u/∂z profile has been calculated by Equation (1). t xz is calculated by Equation (3), ∂w/∂x is neglected and the longitudinal stress deviation (σ x – σ z ) is modelled:
-
(1) using the horizontal velocity profile u(z)from the bore-hole-tilting measurements,
-
(2) assuming the profile form of u(z) to be slowly changing in x along the flow line,
-
(3) using accumulation rates along the flow-line (Reference Reeh, Reeh, Johnsen, Dahl-Jensen, Langway, Langway, Oeschger and DansgaardReeh and others, in press; Reference Ragle and DavisRagle and Davis, 1962).
With these assumptions the left-hand side of Equation (6) ∂u/∂x is given by:

Q being the mass flux determined either by the accumulation rates along the flow line 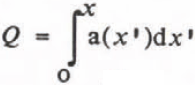 or by the bore-hole tilting measurements
or by the bore-hole tilting measurements  . (σ
x
– σ
z
) is calculated by inserting Equation (7) into Equation (6).
. (σ
x
– σ
z
) is calculated by inserting Equation (7) into Equation (6).
The calculated ∂u/∂z profile (Fig. 3a) agrees with that observed within the measuring accuracy.
In principle, the bore-hole-tilting measurements should reveal a possible deformation effect of the increasing single-maximum c-axis orientation downward in the Holocene ice. However, this effect must be negligible in the Dye 3 area, because the observed increase of ∂u/∂z and B downwards are fully explained by A(T) in the Holocene ice.
Perturbation Modelling of the Ice Deformation
The derived flow-law parameter B is used in a stationary, multi-layer, two-dimensional first-order perturbation model, where deformation is determined by Glen′s flow law (Equations (1) and (6)). As described above, the basal and surface profiles are divided into smoothed profiles and deviations from these. The flow between the smoothed boundaries is called the basic flow. At Dye 3 the stress fields in the basic flow are assumed to be determined as described above, the horizontal velocity by the bore-hole-tilting measurements and the vertical velocity by integration of Glen′s flow law (7) as ∂w/∂z = −∂ u/∂x.
The aim of the perturbation method is to calculate the perturbations of the basic stresses, velocities, and surface profile caused by the basal undulations. The basal undulations, i.e. deviations from the smoothed basal profiles along the A, B, and C lines (Figs 1 and 6c), will serve as the perturbation input in the perturbation model to be outlined below. The A, B, and C lines used in the analysis are restric

Fig. 6. Comparison of the calculated surface undulations and strain-rates with those observed for the A, B, and C lines.
-
(a) 12-component Fourier representation of the modelled strain-rates (full curves). The dashed step curves are the average strain-rates measured by Reference Whillans, Whillans, Jezek, Drew and GundestrupWhillans and others (1984).
-
(b) 12-component Fourier representation of the modelled surface undulations (full curves) and the observed undulations (Reference Overgaard, Gundestrup, Langway, Langway, Oeschger and DansgaardOvergaard and Gundestrup, in press) (dashed curves).
-
(c) Basal deviations from the trend lines in Figure 2b (full curve). A 12-component Fourier representation of the curves (dashed curves) coincides completely with the full curves.
ted as shown in Figure 1 to regions, where the lines follow flow-lines.
The bedrock deviations are resolved in a Fourier series of the form:

where N in this analysis is 12.
For a first-order model, it is possible to calculate the resulting perturbations of the stresses, velocities, and surface elevation for each wavelength separately. Let us choose the following representation of the base:
in which it is assumed that ∊ « 1. The mean base is given by R0(x) = 0, because the x-axis is parallel to this trend line.
This basal perturbation will change the stresses, velocities, and surface elevation into:

where u, w, σ x , σ z , and τXZ are the velocities and the stresses caused by the basic flow. S0(x) is the surface trend line, which is the upper boundary for the basic flow, and the second terms on the right-hand sides are the perturbation terms caused by the basal perturbations (9) (Reference Hutter, Hutter, Legerer and SpringHutter and others, 1981). The basic terms in (9) have an x-variation, so they can describe a "realistic" basic flow between the smoothed boundaries R0(x) and S0(x). In the perturbation model the perturbation terms in Equation (10) will be considered to be sinusoidal in x due to the harmonic basal perturbation given by Equation (9). this requires the x-variation of the basic terms to be small compared to the perturbation terms, which limits the wavelengths in Equation (9) to a length scale not asymptotically large compared with the ice thickness. The resulting perturbation model however yields more "realistic" results by allowing the basic flow a small x-dependence instead of using a theoretically more correct basic flow independent of x (Reference HutterHutter, [c1983]; Reference Reeh, Reeh, Johnsen, Dahl-Jensen, Langway, Langway, Oeschger and DansgaardReeh and others, in press).
If the representations (10) are substituted into the field-equations (balance laws of mass and momentum, and Glen′s flow law given by Equations (1) and (6)), and if the terms of equal powers of ∊ are collected, the first-order field equations are as follows:

F1, F2, and F3 depend on the basic stresses:

where the basic shear stress τxzo is determined by Equation (3) and the longitudinal stress deviation (σ xo – σ zo )is modelled as described above.
As to boundary conditions, the velocities are assumed to be zero at the base, the ice temperature being below the pressure-melting point (–13°C; Reference Gundestrup and HansenGundestrup and Hansen, 1984), and at the surface the stresses must be continuous. Furthermore, the surface must satisfy the conditions of a kinematic surface. Hence, the boundary conditions are:

a being the accumulation rate at Dye 3.
The first-order boundary conditions for the field Equations (11) are derived by substituting Equations (9) and (10) into the boundary conditions (12) and approximating them to the conditions at the mean base R 0 (x) and surface S0(x) by Taylor series expansions. Note that the surface perturbations S1(x) appearing in the approximated boundary conditions are considered as unknown.
The field Equations (11) were also used in the modelling by Reference Reeh, Reeh, Johnsen, Dahl-Jensen, Langway, Langway, Oeschger and DansgaardReeh and others (in press). However in that study F 1 was neglected, and F 2 was put approximately equal to F 3, the depth variation of which was approximated by an exponential variation. In this study the latter, rather rough approximation is avoided and the ice is divided into M layers, in which F 2, F 3, and B are assumed to be constant (Fig. 4). The terms containing F 1 are still neglected as they are an order of magnitude smaller than the terms containing F 2 and F 3 near the base, where (σ xo – σ zo ) « T xz0 (Reference Dahl-JensenDahl-Jensen, unpublished).

Fig. 4. Definition of the coordinate systems used in the perturbation model.
With these three assumptions the mth layer has the following field equations:

These field equations are nearly identical to the field equations for a Newtonian viscous fluid and can be solved accordingly by the use of the stress function (Reference Hutter, Hutter, Legerer and SpringHutter and others, 1981). The field equations have an analytical solution because ![]() and
and ![]() are assumed constant in each layer. It is an advantage to have analytical solutions, still with the use of non-linear rheology. It greatly simplifies the problem, and hence it is more feasible for computer calculations.
are assumed constant in each layer. It is an advantage to have analytical solutions, still with the use of non-linear rheology. It greatly simplifies the problem, and hence it is more feasible for computer calculations.
As boundary conditions between the layers it is assumed that

The M systems of field equations, and the corresponding boundary conditions, define the first-order boundary-value problem. As the x-variation of the first-order solution is entirely caused by the harmonic form of the basal perturbation ϵR1(x) = ϵH0 cos ωx, the expressions for the resulting perturbations will also be sinusoidal in x, with the same frequency. Specifically, the surface perturbation ϵS1(x) will be sinusoidal, and with a phase shift Φ(ω) relative to the base perturbation:
where the functions

and
are called the filter function and the phase shift, respectively. When used on the basal Fourier series (9), they produce a Fourier series for the surface undulations.
Results
Calculations of the filter function and the phase shift for the Dye 3 region are shown in Figure 5.

Fig. 5. The filter function and the phase shift calculated by the model for the Dye 3 region.
The filter function increases with the wavelength λ between 5 and 25 km (Fig. 5). The phase shifts are close to – π/2 for λ> 4 km.
Comparison with the observed surface deviations (Fig. 6b) shows good agreement for the A, B, and C lines in Figure 1. The dominating wavelength of the surface and basal undulations is 8 km (4H 0), so with the basal amplitudes being of the order of 100 m (cf. Fig. 6c), the surface amplitudes are of the order of 4 to 5 m. As the Fourier-resolved bases are non-periodic and have different values at the beginning and the end of the regions considered, disagreement between the calculated and true surface must be expected over the first 4 km and the last 4 km.
Analyses show that the filter function is very sensitive to the B-profile. Using the exponential form of the flow-law parameter, as in the previous model (Reference Reeh, Reeh, Johnsen, Dahl-Jensen, Langway, Langway, Oeschger and DansgaardReeh and others, in press), the filter-function values become 50% lower. The disagreement in the previous model is believed to be due to the applied B-profile, rather than to non-stationarity, or to the two-dimensional approximation, or to the rather big basal undulations (0.15H 0) in the first-order model.
Use of a B-profile where the c-axis orientation also affects the enhancement factor as suggested by Reference Russell-Head and BuddRussell-Head and Budd (1979) gives filter-function values 30% higher than those observed for the dominating wavelengths.
The calculated surface strain-rates ∂u/∂x have amplitudes of the order of 3 × 10−4 year−1, which is of the same order as the mean strain-rates in the Dye 3 region (Reference Whillans, Whillans, Jezek, Drew and GundestrupWhillans and others, 1984). The perturbation terms of the surface strain-rates are in phase with the surface undulations, having a phase shift of – π/2 relative to the base. Although the measured strain-rates (step curves in Figure 6a) are only average values over 2 km, the calculated strain-rate amplitudes seem to be too big. This might be expected (in particular for wavelengths smaller than 3H 0 = 6 km) in view of the approximations in the first-order perturbation theory, which are more serious for calculation of surface strain-rates than for calculation of surface undulations, as will be discussed in a forthcoming paper.
Summary and Conclusions
The flow-law parameter derived from the Dye 3 bore-hole-tilting measurements is divided into a temperature-dependent factor and an enhancement factor that depends on other ice parameters. The enhancement factor is equal to unity in the Holocene ice (the upper 1780 m of the core), and it has a mean value of three in the underlying Pleistocene ice. The high values of the enhancement factor in the Pleistocene ice are believed to be due to the high concentration of dust and other impurities, and to small crystal size. The c-axis orientation does not seem to affect the deformation rates.
The dramatic change of the enhancement factor at the Holocene/Pleistocene transition is essential for modelling the present and past flow of the Greenland ice sheet, because the easy-flowing layer of ice has been becoming thinner and thinner, ever since the end of the last glaciation.
The perturbation model described above divides the ice into layers, within which the flow-law parameter is assumed to be constant. The perturbation model has analytical solutions in each layer, which limits the required computer time. The number of layers can be chosen to agree with the amount of information available regarding the flow-law parameter.
The flow-law parameter derived from the Dye 3 deep-hole measurements, and the basal topographic observations are used as inputs in the perturbation model to predict the surface profile and the strain-rates. The agreement with the observed surface profiles and strain-rates shows that the applied flow-law parameter profile is realistic.
Analyses show, that the results from the perturbation model are very sensitive to the flow-law parameter used as an input. Beyond being used with a basic flow model, to calculate the age-depth relationship and the flow, the perturbation model can be used on other flow lines where base and surface profiles are known, to estimate the flow-law parameter -versus depth.
Acknowledgements
The Department of Physical Glaciology, Geophysical Institute, have given valuable help and discussions. Lyle Hansen and Niels Gundestrup very kindly provided the data from the logging of the Dye 3 deep hole. This work has been funded by Danish Natural Science Research Council and the European Economic Community, XII Directorate General (Contract CLI.D67DK.1).








