Imaging spectroscopy is emerging as a critical tool in our ability to move beyond simple detection of changes in cryosphere–climate interactions to attribution of these changes to forcings by changes in greenhouse gases and absorbing impurities (Reference Dozier, Green, Nolin and PainterDozier and others, 2009; Reference Singh, Kulkarni and ChaudharySingh and others, 2010). Fresh in the growing literature related to imaging spectroscopy of snow and ice, Reference Singh, Kulkarni and ChaudharySingh and others (2010) have explored the impact of dust on the hyperspectral reflectance of snow with the intent of understanding the capacity of imaging spectroscopy to quantify snow properties. The paper reaches relatively robust conclusions about the impact of soil on snow reflectance. As such, the efforts of the authors and the importance of their paper in providing foundational work on imaging spectroscopy of the cryosphere should be appreciated.
However, there are aspects of the paper that are erroneous due to erroneous data interpretations. Because these interpretations are not uncommon, but as far as I know have never been directly addressed in the literature, I will address them here. This comment focuses on two erroneous interpretations of the spectral data: (1) that the stepwise drop in retrieved reflectance near 1000 nm wavelength is a meaningful indicator of changes in the physical properties of the snowpack; and (2) that the dramatic differences in reflectance in the visible wavelengths can be attributed to increases in grain size. Reference Singh, Kulkarni and ChaudharySingh and others (2010) are not alone in the literature in making these erroneous interpretations. We discuss the details below and comment on issues related to the inference of albedo and levels of dust concentration.
In Figure 1, I show Reference Singh, Kulkarni and ChaudharySingh and others’ (2010) figure 3 in which they have plotted what they term ‘snow reflectance’ for a range of applications of contaminants from 0 to 95.54 mg cm −2. The use of the ambiguous term ‘snow reflectance’ ultimately leads to the erroneous interpretation described in point 2 above. The compelling and valid result here is that at higher concentrations of soil, the band depth of the ice-absorption feature near 1025 nm wavelength is reduced, whereas actual snow grain size is most likely unchanged or increasing (Fig. 1). It is this band that is often integrated and mapped to optical grain radius (Reference Clark and RoushClark and Roush, 1984; Reference Nolin and DozierNolin and Dozier, 2000; Reference Painter, Molotch, Cassidy, Flanner and SteffenPainter and others, 2007). Therefore, at these higher soil concentrations, retrievals of grain size from this absorption feature will be unreliable.
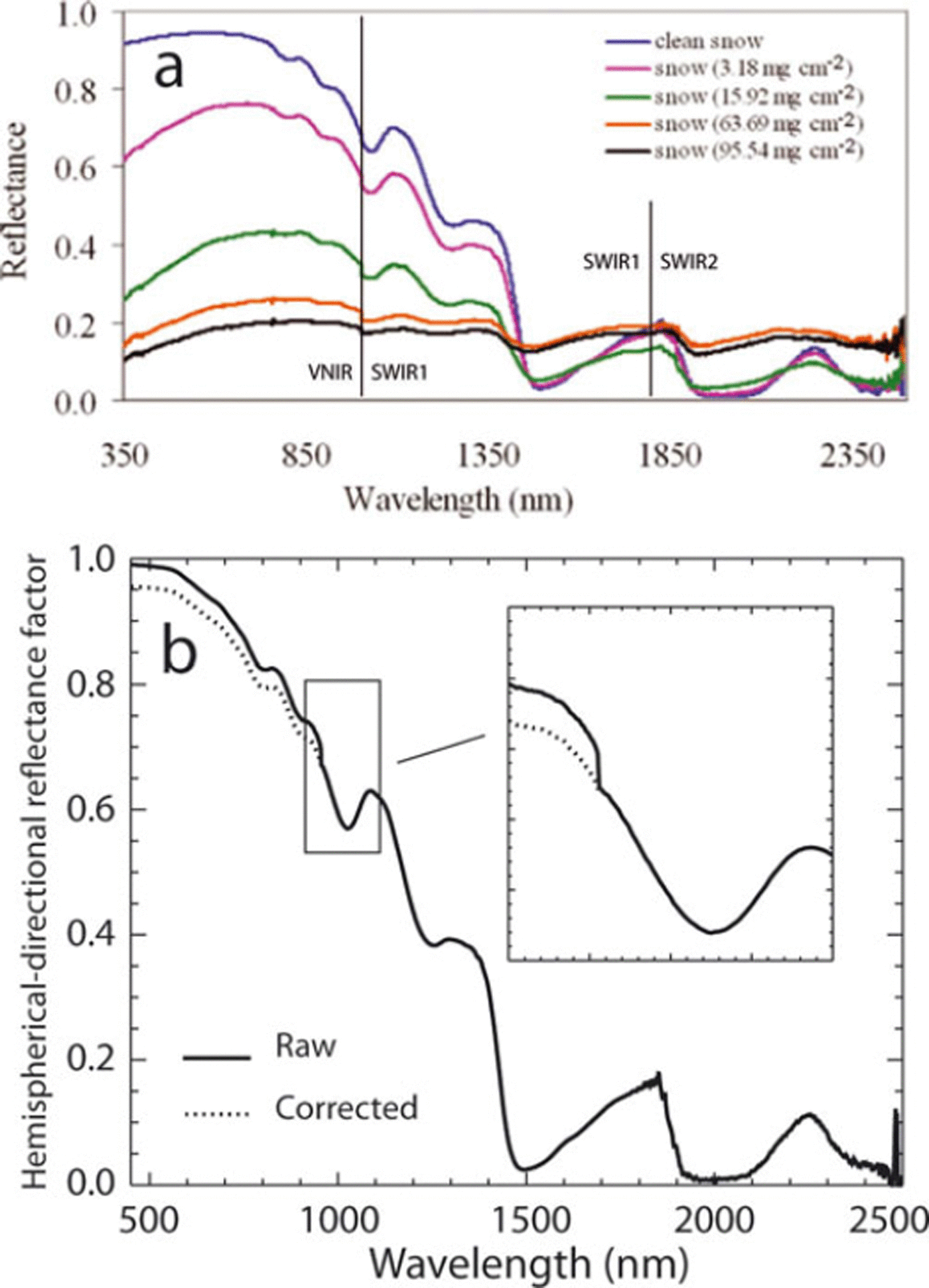
Fig. 1. (a) Spectra of snow with varying soil concentrations from figure 1 of Reference Singh, Kulkarni and ChaudharySingh and others (2010). Note the abrupt steps in the ice absorption feature near 1025 nm. The splices between VNIR SWIR1 and between SWIR1 and SWIR2 are indicated. (b) Snow HCRF from the Colorado Rocky Mountains (Senator Beck Basin) collected with the author’s ASD field spectroradiometer. Note that the splice between VNIR and SWIR1 is at a shorter wavelength because the instrument is older.
The error comes, however, in the interpretation of the stepwise drop in reflectance at 1000 nm (Fig. 1). This step in the spectrum results not from a spectral discontinuity in the optical properties of ice (Reference Warren and BrandtWarren and Brandt, 2008) or the soil, but instead from a known but correctable artifact of the instrument optical geometry (http://www.asdi.com). The optic cable of the ASD (Analytical Spectral Devices, Inc.) Field Spec spectroradiometer has an anisotropic distribution of the wavelength-dependent fibers that creates a sampling scenario in which different areas of the surface are observed with different parts of the spectrum. Without a randomizing filter, this often results in stepwise differences between the ASD FieldSpec VNIR (Si), SWIR1 (InGaAs) and SWIR2 (InGaAs) spectrometers that have wavelength ranges of 350–1000 nm, 1001–1800 nm and 1801–2500 nm, respectively. The step between VNIR and SWIR1 is most pronounced as seen in Reference Singh, Kulkarni and ChaudharySingh and others’ (2010) figures 1, 5, and 6, with stepwise drops in directional reflectance, continuum removal and the first derivative. The bias of VNIR higher than SWIR1 at the splice in Reference Singh, Kulkarni and ChaudharySingh and others’ (2010) spectra is consistent with my observations. The reason for this bias is not entirely clear, but it may result from the slightly larger angular field of view of the VNIR fibers that will then be more sensitive to the forward-scattering peak in the distribution of the hemispherical–conical reflectance factor (HCRF) of snow (Reference WarrenWarren, 1982; Painter and Dozier, 2004; Reference Schaepman-Strub, Schaepman, Painter, Dangel and MartonchikSchaepman-Strub and others, 2006).
Given that Reference Singh, Kulkarni and ChaudharySingh and others’ (2010) figure 2 shows a moderately rough surface that creates local shadowing, changes in irradiance and local changes in the HCRF, one would expect steps in the spectrum at the VNIR/SWIR1 splice. The heterogeneous distribution or clumping of soil could also increase the likelihood of differences in surface directional reflectances that result in discontinuous spectra such as those shown. The photographs of snow surfaces without and with considerable soil concentrations in my Figure 2 demonstrate similar spatial heterogeneity in local illumination, HCRF and soil concentration. As the authors indicate, they use a 25° field-of-view (FOV) bare fiber, so at 30 cm above the ground the ground instantaneous field of view has a diameter of ∼13 cm or approximately a side of the Spectralon panel shown in my Figure 2. The spatial heterogeneity evident in both panels of Figure 2 would likely affect a step in the reflectance. Without correction of the step in the spectrum, the calculations of feature asymmetry and band strength are erroneous, although the overall qualitative conclusions in Reference Singh, Kulkarni and ChaudharySingh and others (2010) are likely correct.

Fig. 2. (a) Relatively clean snow surface in Khumbu Himal, Nepal, with Spectralon reflectance panel for calibration of raw image (photo courtesy of S. Kaspari, Central Washington University). Despite the relatively clean surface, the heterogeneity in surface roughness results in local changes in directional reflectance. (b) Dust-laden snow in Colorado Rockies with Spectralon reflectance panel (photo: Snow Optics Laboratory).
To avoid this problem, the manufacturer distributes a fiber-optic scrambler that homogenizes the signal with respect to the spectrum. However, for those measurements made without the fiber-optic scrambler, one must use the data themselves to remove the step in the spectrum. Given that the step is driven by the different parts of the spectrum looking at slightly different targets, the concept of ‘correcting the spectrum’ does not apply, i.e. each spectrum subset is correct but for different targets. Therefore, one must decide how to modify the data in order to create a continuous spectrum, and hence no method is uniquely correct.
My standard post-processing procedure has been to use a linear fit to the three shortest-wavelength bands of the SWIR1 to determine where the longest-wavelength band of the visible/near-infrared (VNIR) spectrum should be and scale the VNIR spectrum accordingly (Fig. 1b). This technique is used because of the greater thermal-driven signal drift in the VNIR silicon detector (particularly in colder settings) relative to the SWIR1. However, the best solution is to use the randomizing fiber-optic scrambler for static measurements from a tripod or other fixed platform to avoid the need to make a decision for modifying the data.
The second error in interpretation comes in Reference Singh, Kulkarni and ChaudharySingh and others’ (2010) figure 4 (my Fig. 3), in which the reflectance differences are attributed to differences in grain size. The spectra suggest a substantial drop in reflectance throughout the shortwave spectrum, with an increase in grain size from <0.5 mm to <1.0 and 1.0–2.0 mm. While the drop in near-infrared (NIR) and shortwave infrared (SWIR) HCRF could be attributable to changes in grain size, the drop in visible HCRF for relatively clean snow is inconsistent with the optical properties of ice. In the visible wavelengths, the imaginary part of the complex refractive index of ice lies between 10−11 and 10−7 (Reference Warren and BrandtWarren and Brandt, 2008). For any of the grain sizes <0.5 to 2 mm, the single-scattering albedo of grains in the visible wavelengths is >0.9999. Therefore, the spectral albedo and directional reflectances in the visible spectrum are only slightly sensitive to changes in grain size in the range described for these measurements (Reference Warren and WiscombeWarren and Wiscombe, 1980).
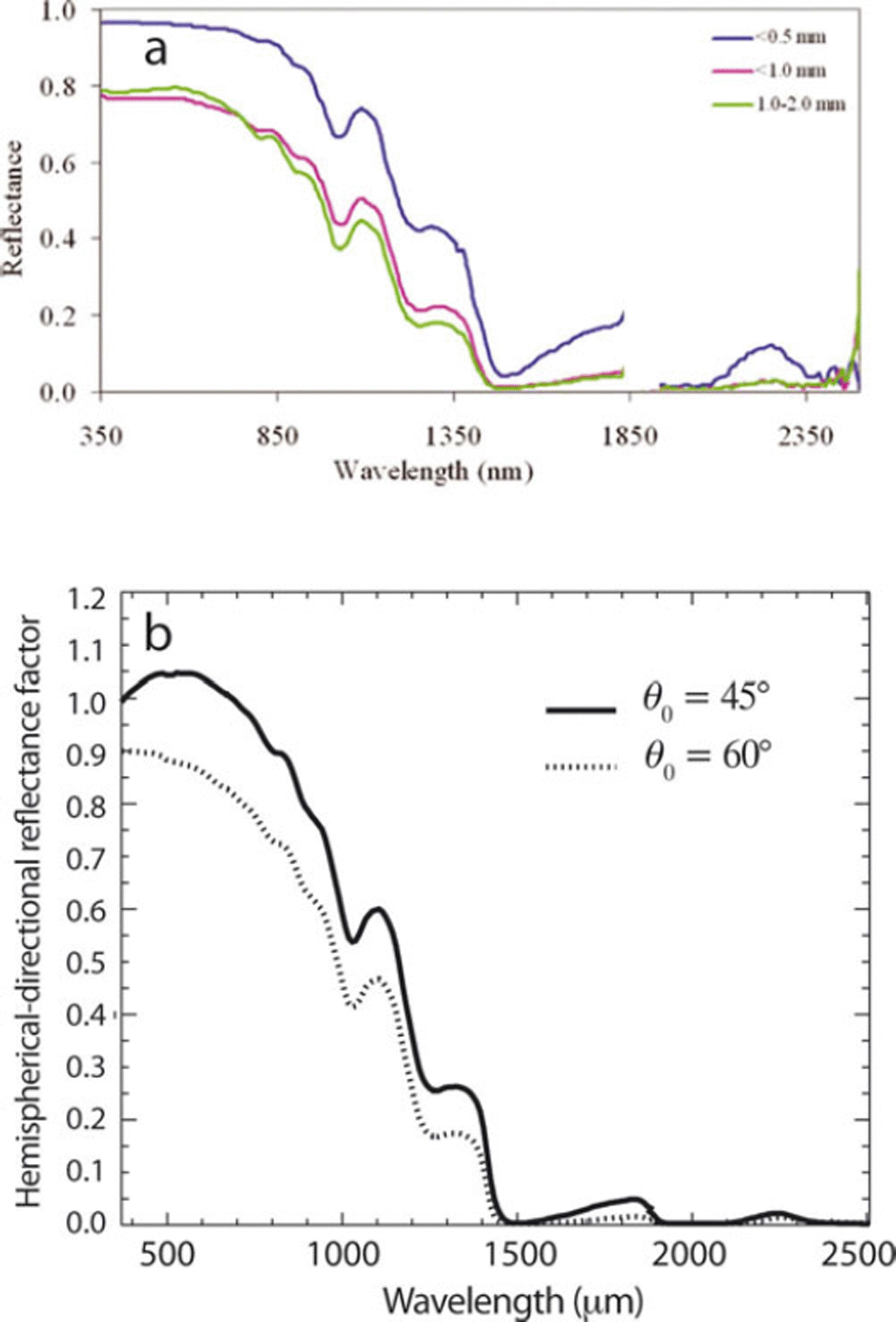
Fig. 3. (a) HCRF of snow for different grain sizes (fig. 4 from Reference Singh, Kulkarni and ChaudharySingh and others, 2010). (b) By contrast, nadir HDRF (hemispherical–directional reflectance factor) for different solar zenith angles but the same grain size, exhibiting differences similar to those in (a).
However, it is likely that the differences observed in the spectra are due to nadir observations of HCRF from the snow surface illuminated with different solar zenith angles. In particular, it appears that the spectra for the larger grain sizes in Figure 3a were collected when illumination had a larger solar zenith angle. Figure 3b compares Figure 3a with modeled nadir spectra for clean snow with identical grain size and morphology but solar zenith angles of 45° and 60° (Painter and Dozier, 2004). These show that it is plausible that the differences in spectra presented in Reference Singh, Kulkarni and ChaudharySingh and others’ (2010) figure 4 resulted from differences in solar zenith angle but Singh and others did not describe the solar zenith angles during spectra acquisitions. Another possible explanation could be that the observed surface for the larger grain sizes was tilted away from the sun under identical global solar zenith angle but with a larger local solar zenith angle. Ultimately, the latter two scenarios are far more likely than the direct effect of grain size on the visible HCRF, which would contradict radiative transfer theory, the known optical properties of ice, and all previous field measurements (Reference Warren and WiscombeWarren and Wiscombe, 1980).
A description of the retrieval or inference of snow albedo is missing. Given that Reference Singh, Kulkarni and ChaudharySingh and others (2010) do not mention the use of a cosine receptor for the spectrometer, and the described distribution of soil on the snow surface could not cover an area sufficiently large for a robust hemispherical measurement, it appears that the HCRF spectrum was convolved with the irradiance spectrum and then integrated to albedo. Because the nadir spectrum is sensitive to the solar zenith angle and most often is not equivalent to the spectral albedo because of spectrally sensitive, anisotropic reflectance, these results are most likely in error.
Finally, the concentrations described as being small (<15 mg cm −2, i.e. <150 g m−2) are not small, even in regions of considerable dust deposition. For example, dust loading to mountain snow cover in the San Juan Mountains of Colorado, USA, in the spring of 2009 just exceeded 80 g m−2, and yet albedo determined with paired broadband shortwave pyranometers dropped considerably below 0.35 at full exposure of the dust load (unpublished data). The influence of dust on the HCRF and albedo of snow is determined not only by the concentration but also by the dust optical properties (i.e. complex refractive index), snow grain size, relative internal and external mixtures of dust with snow grains, and the solar zenith angle and distribution of diffuse to direct irradiance.
In summary, this comment is not meant to be critical of the efforts of Reference Singh, Kulkarni and ChaudharySingh and others (2010) but to remedy some of the interpretations that they made, that others before them (including this author) have made and likely others after them (hopefully fewer) will make. As Reference Singh, Kulkarni and ChaudharySingh and others (2010) indicate, the growing use of field and imaging spectrometers necessitates that we converge on common understandings of instrumentation as well as of changes in directional reflectance and albedo due to changes in snow physical state and light-absorbing impurities.
Acknowledgements
Part of this work was performed at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA.
15 October 2010





