Article
 A module calculus for Pure Type Systems
A module calculus for Pure Type Systems
-
- Published online by Cambridge University Press:
- 04 May 2006, pp. 287-352
-
- Article
-
- You have access
- Export citation
An object-oriented calculus with term constraints
-
- Published online by Cambridge University Press:
- 04 January 2007, pp. 353-386
-
- Article
-
- You have access
- Export citation
Warnings for pattern matching
-
- Published online by Cambridge University Press:
- 15 February 2007, pp. 387-421
-
- Article
-
- You have access
- Export citation
Book Review
SMIL 2.0 Interactive Multimedia for Web and Mobile Devices by C. A. Dick Bulterman and Lloyd Rutledge, Springer X.media.publishing, 2004, 440pp, ISBN 3-540-20234-X
-
- Published online by Cambridge University Press:
- 15 February 2007, pp. 423-424
-
- Article
-
- You have access
- Export citation
Programming Languages and Operational Semantics by Fernández Maribel, King's College Publications, 2004, ISBN 0954300637
-
- Published online by Cambridge University Press:
- 15 February 2007, pp. 424-426
-
- Article
-
- You have access
- Export citation
The Haskell School of Expression by Hudak Paul, Cambridge Univerity Press, 2000 1
-
- Published online by Cambridge University Press:
- 15 February 2007, pp. 426-428
-
- Article
-
- You have access
- Export citation
Inductive Synthesis of Functional Programs by U. Schmid, Springer Verlag, 2003, 420pp, ISBN 3540401741
-
- Published online by Cambridge University Press:
- 15 February 2007, pp. 428-429
-
- Article
-
- You have access
- Export citation


 A module calculus for Pure Type Systems
A module calculus for Pure Type Systems
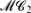 , adapted from SML-like module systems for programming languages. This system gives a theoretical framework addressing the issues mentioned above in a quite uniform way. It is intended to be a theoretical foundation for the module systems of proof-assistants such as Coq or Agda. We show how reliability and usability can be formalized as metatheoretical properties and prove they hold for
, adapted from SML-like module systems for programming languages. This system gives a theoretical framework addressing the issues mentioned above in a quite uniform way. It is intended to be a theoretical foundation for the module systems of proof-assistants such as Coq or Agda. We show how reliability and usability can be formalized as metatheoretical properties and prove they hold for