Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Barendregt, Henk
1993.
Constructive proofs of the range property in lambda calculus.
Theoretical Computer Science,
Vol. 121,
Issue. 1-2,
p.
59.
Berarducci, Alessandro
and
Intrigila, Benedetto
1993.
Some new results on easy lambda-terms.
Theoretical Computer Science,
Vol. 121,
Issue. 1-2,
p.
71.
Ariola, Zena
Kennaway, Richard
Klop, Jan Willem
Sleep, Ronan
and
Vries, Fer-Jan
1994.
Theoretical Aspects of Computer Software.
Vol. 789,
Issue. ,
p.
543.
Barendregt, Henk
1995.
Enumerators of lambda terms are reducing constructively.
Annals of Pure and Applied Logic,
Vol. 73,
Issue. 1,
p.
3.
1995.
European Summer Meeting of the Association for Symbolic Logic.
Bulletin of Symbolic Logic,
Vol. 1,
Issue. 1,
p.
85.
Kennaway, Richard
van Oostrom, Vincent
and
de Vries, Fer-Jan
1996.
Algebraic and Logic Programming.
Vol. 1139,
Issue. ,
p.
254.
Kerth, Rainer
1998.
The interpretation of unsolvable λ-terms in models of untyped λ-calculus.
Journal of Symbolic Logic,
Vol. 63,
Issue. 4,
p.
1529.
Kesner, Delia
2007.
Computer Science Logic.
Vol. 4646,
Issue. ,
p.
238.
Bucciarelli, A.
Carraro, A.
Favro, G.
and
Salibra, A.
2016.
Graph easy sets of mute lambda terms.
Theoretical Computer Science,
Vol. 629,
Issue. ,
p.
51.
Xu, Kevin H.
2017.
A class of bounded functions, a database language and an extended lambda calculus.
Theoretical Computer Science,
Vol. 691,
Issue. ,
p.
81.
Barendregt, Henk
Endrullis, Jörg
Klop, Jan Willem
and
Waldmann, Johannes
2017.
Raymond Smullyan on Self Reference.
Vol. 14,
Issue. ,
p.
67.
TERWIJN, SEBASTIAAN A.
2018.
GENERALIZATIONS OF THE RECURSION THEOREM.
The Journal of Symbolic Logic,
Vol. 83,
Issue. 04,
p.
1683.
Barendregt, Henk
and
Terwijn, Sebastiaan A.
2019.
Fixed point theorems for precomplete numberings.
Annals of Pure and Applied Logic,
Vol. 170,
Issue. 10,
p.
1151.
TERWIJN, SEBASTIAAN A.
2020.
COMPUTABILITY IN PARTIAL COMBINATORY ALGEBRAS.
The Bulletin of Symbolic Logic,
Vol. 26,
Issue. 3-4,
p.
224.
Terwijn, Sebastiaan A.
2020.
The noneffectivity of Arslanov’s completeness criterion and related theorems.
Archive for Mathematical Logic,
Vol. 59,
Issue. 5-6,
p.
703.
Arrial, Victor
Guerrieri, Giulio
and
Kesner, Delia
2024.
Genericity Through Stratification.
p.
1.
Accattoli, Beniamino
and
Lancelot, Adrienne
2024.
Foundations of Software Science and Computation Structures.
Vol. 14575,
Issue. ,
p.
24.
Faizrahmanov, Marat
2025.
Some properties of precompletely and positively numbered sets.
Annals of Pure and Applied Logic,
Vol. 176,
Issue. 2,
p.
103523.
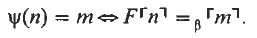 There are several proposals for what F⌜n⌝ should be in case ψ(n) is undefined: (1) a term without a normal form (Church); (2) an unsolvable term (Barendregt); (3) an easy term (Visser); (4) a term of order 0 (Statman).
There are several proposals for what F⌜n⌝ should be in case ψ(n) is undefined: (1) a term without a normal form (Church); (2) an unsolvable term (Barendregt); (3) an easy term (Visser); (4) a term of order 0 (Statman).


Discussions
No Discussions have been published for this article.