Article contents
Correctness of compiling polymorphism to dynamic typing*
Published online by Cambridge University Press: 12 December 2016
Abstract
The connection between polymorphic and dynamic typing was originally considered
by Curry et al. (1972, Combinatory Logic, vol.
ii) in the form of “polymorphic type assignment” for untyped
λ-terms. Types are assigned after the fact to what is, in modern
terminology, a dynamic language. Interest in type assignment was revitalized by
the proposals of Bracha et al. (1998, OOPSLA) and Bank
et al. (1997, POPL) to enrich Java with polymorphism
(generics), which in turn sparked the development of other languages, such as
Scala, with similar combinations of features. In such a setting, where the
target language already has a monomorphic type system, it is desirable to
compile polymorphism to dynamic typing in such a way that as much static typing
as possible is preserved, relying on dynamics only insofar as genericity is
actually required. The basic approach is to compile polymorphism using
embeddings from each type into a universal “top” type, 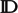 ${\mathbb{D}}$, and partial projections that go in the
other direction. This scheme is intuitively reasonable, and, indeed, has been
used in practice many times. Proving its correctness, however, is non-trivial.
This paper studies the compilation of System F to an
extension of Moggi's computational meta-language with a dynamic type and shows
how the compilation may be proved correct using a logical relation.
${\mathbb{D}}$, and partial projections that go in the
other direction. This scheme is intuitively reasonable, and, indeed, has been
used in practice many times. Proving its correctness, however, is non-trivial.
This paper studies the compilation of System F to an
extension of Moggi's computational meta-language with a dynamic type and shows
how the compilation may be proved correct using a logical relation.
- Type
- Theoretical Pearls
- Information
- Copyright
- Copyright © Cambridge University Press 2016
Footnotes
This research is sponsored in part by the National Science Foundation under Grant Number 1116703. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
References
- 1
- Cited by



Discussions
No Discussions have been published for this article.