Article contents
Boxes go bananas: Encoding higher-order abstract syntax with parametric polymorphism*
Published online by Cambridge University Press: 01 January 2008
Abstract
Higher-order abstract syntax is a simple technique for implementing languages with functional programming. Object variables and binders are implemented by variables and binders in the host language. By using this technique, one can avoid implementing common and tricky routines dealing with variables, such as capture-avoiding substitution. However, despite the advantages this technique provides, it is not commonly used because it is difficult to write sound elimination forms (such as folds or catamorphisms) for higher-order abstract syntax. To fold over such a data type, one must either simultaneously define an inverse operation (which may not exist) or show that all functions embedded in the data type are parametric. In this paper, we show how first-class polymorphism can be used to guarantee the parametricity of functions embedded in higher-order abstract syntax. With this restriction, we implement a library of iteration operators over data structures containing functionals. From this implementation, we derive “fusion laws” that functional programmers may use to reason about the iteration operator. Finally, we show how this use of parametric polymorphism corresponds to the Schürmann, Despeyroux and Pfenning method of enforcing parametricity through modal types. We do so by using this library to give a sound and complete encoding of their calculus into System 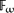 . This encoding can serve as a starting point for reasoning about higher-order structures in polymorphic languages.
. This encoding can serve as a starting point for reasoning about higher-order structures in polymorphic languages.
- Type
- Articles
- Information
- Copyright
- Copyright © Cambridge University Press 2007
References
- 24
- Cited by



Discussions
No Discussions have been published for this article.