In this work, the relationship between the velocity of an elongated bubble and its shape is investigated, in the case where the elongated bubble flows in a viscous liquid initially at rest in a pipe. The velocity, expressed as a Froude number, depends on the angle of the inclined pipe, the Eötvös number and the buoyancy Reynolds number. The diameter of the pipe and the surface tension being fixed, the Eötvös number remains constant; this study focuses on the dependence of the velocity on the pipe inclination angle and the viscosity of the liquid. The velocity of the elongated bubble was measured for different angles between 0 and 15 degrees and for liquid viscosities 10 to 200 times that of water. As the velocity of elongated bubbles depends closely on their shape, shadowgraphy coupled with particle image velocimetry was used. The results show that the velocity of the elongated bubbles is highly sensitive to the inclination angle of the pipe and to the viscosity of the liquid, particularly for low pipe inclinations and large viscosities. In the layer of liquid located downstream of the elongated bubble, laminar flow develops rapidly in the liquid, resulting from a balance between gravity and friction at the wall. The identification of the position of the stagnation point close to the nose of the elongated bubble and the curvature of the interface at this point helps to explain why the velocity of the elongated bubble decreases for low angles and high viscosities.

Heat and mass transports through a rough surface are among the most fundamental and important phenomena in either natural or engineering problems. In this paper, theoretical modelling and direct simulation Monte Carlo method are employed to study the heterogeneous reaction–diffusion features induced by microscale roughness which is comparable to the molecular mean free path of the ambient gas. A quasi-one-dimensional homogeneous model is proposed, and it consists of an external diffusion region outside the roughness elements and an internal reaction–diffusion region which could be equivalent to a smooth surface with an effective chemical property. The external macroscopic diffusion can be characterized by a non-equilibrium criterion – the Damköhler number. The internal diffusion in micro-cavities must be analysed by considering the rarefied gas effects on the diffusivity, and another non-equilibrium criterion, the Thiele number, is introduced to evaluate the effective boundary condition imposed on the external region. Analytical formulae based on these criteria are derived to predict the equivalent surface reaction–diffusion performance, and the predictions compare well with the numerical results of different types of surface reaction, even on the three-dimensional roughness. This reveals that the roughness could either enhance or weaken the apparent reaction rate depending on the non-equilibrium degree. This study could enrich our understanding of the gas–surface interactions on a rough wall, such as the oxidation, catalysis and energy accommodation, and also preliminarily provides a practical method for evaluation of the aerothermochemical performance of coating materials of hypersonic vehicles.

Shock-tube experiments and theoretical studies have been performed to highlight mode-coupling in an air–SF$_6$–air fluid layer. Initially, the two interfaces of the layer are designed as single mode with different basic modes. It is found that as the two perturbed interfaces become closer, interface coupling induces a different mode from the basic mode on each interface. Then mode coupling further generates new modes. Based on the linear model (Jacobs et al., J. Fluid Mech., vol. 295, 1995, pp. 23–42), a modified model is established by considering the different accelerations of two interfaces and the waves’ effects in the layer, and provides good predictions to the linear growth rates of the basic modes and the modes generated by interface coupling. It is observed that interface coupling behaves differently to the nonlinear growth of the basic modes, which can be characterized generally by the existing or modified nonlinear model. Moreover, a new modal model is established to quantify the mode-coupling effect in the layer. The mode-coupling effect on the amplitude growth is negligible for the basic modes, but is significant for the interface-coupling modes when the initial wavenumber of one interface is twice the wavenumber of the other interface. Finally, amplitude freeze-out of the second single-mode interface is achieved theoretically and experimentally through interface coupling. These findings may be helpful for designing the target in inertial confinement fusion to suppress the hydrodynamic instabilities.

This paper studies the instability of two-dimensional magnetohydrodynamic systems on a sphere using analytical methods. The underlying flow consists of a zonal differential rotation and a toroidal magnetic field is present. Semicircle rules that prescribe the possible domain of the wave velocity in the complex plane for general flow and field profiles are derived. The paper then sets out an analytical study of the ‘clamshell instability’, which features field lines on the two hemispheres tilting in opposite directions (Cally, Sol. Phys., vol. 199, 2001, pp. 231–249). An asymptotic solution for the instability problem is derived for the limit of weak shear of the zonal flow, via the method of matched asymptotic expansions. It is shown that when the zonal flow is solid body rotation, there exists a neutral mode that tilts the magnetic field lines, referred to as the ‘tilting mode’. A weak shear of the zonal flow excites the critical layer of the tilting mode, which reverses the tilting direction to form the clamshell pattern and induces the instability. The asymptotic solution provides insights into properties of the instability for a range of flow and field profiles. A remarkable feature is that the magnetic field affects the instability only through its local behaviour in the critical layer.

In this research, highly disturbed turbulent flow of distinct three-dimensional characteristics in a square duct with inclined or V-shaped ribs mounted on one wall is investigated using direct numerical simulation. The turbulence field is highly sensitive to not only the rib geometry but also the boundary layers developed over the side and top walls. In a cross-stream plane secondary flows appear as large longitudinal vortices in both inclined and V-shaped rib cases due to the confinement of four sidewalls of the square duct. However, owing to the difference in the pattern of cross-stream secondary flow motions, the flow physics is significantly different in these two ribbed duct cases. It is observed that the mean flow structures in the cross-stream directions are asymmetrical in the inclined rib case but symmetrical in the V-shaped rib case, causing substantial differences in the momentum transfer across the spanwise direction. The impacts of rib geometry on near-wall turbulence structures are investigated using vortex identifiers, joint probability density functions between the streamwise and vertical velocity fluctuations, statistical moments of different orders, spatial two-point autocorrelations and velocity spectra. It is found that near the leeward and windward rib faces, the mean inclination angle of turbulence structures in the V-shaped rib case is greater than that of the inclined rib case, which subsequently enhances momentum transport between the ribbed bottom wall and the smooth top wall.

Underwater stability of an air layer trapped in a micro-structure, plastron, is critical in drag reduction applications. Here, we investigate the wetting state and plastron stability of underwater superhydrophobic surfaces (SHS) under an intense acoustic drive. Flat surfaces and SHS are subjected to short acoustic pulses of different intensities. At low amplitude, the comparison between the results of various surfaces shows that plastron behaves like a water–air interface, whose presence can be detected from the phase of the reflected acoustic waves. At moderate intensity, a wetting transition towards a completely wetting state is observed and shown to be triggered by a sufficiently large acoustic radiation pressure. This wetting transition is well captured by a simplified model by balancing radiation pressure with the critical capillary pressure for the interface sliding. Cavitation clouds appear under strong excitation; their sizes and positions greatly depend on the surface acoustic boundary condition. For SHS in a Cassie–Baxter state (with an air layer), cavitation clouds appear at specific locations (from the solid surface) corresponding to the pressure anti-node of the transient standing wave generated by the reflection. This study unprecedentedly demonstrates the capability of acoustic waves to monitor and characterize plastron stability with low and moderate amplitudes, respectively.

Turbulent boundary layers (TBLs) over surface perturbations like bumps with roughness – notably altering heat and mass transfer, drag, etc. – are prevalent in nature (mountains, dunes, etc.) and technology. We study a channel flow with a transverse bump on one wall superimposed with small-scale longitudinal grooves via direct numerical simulation (DNS) of incompressible flow. Turbulence statistics and dynamics are compared between grooved wall (GW) and smooth wall (SW) bumps. Streamwise spinning jets emanating from the crests’ corners alter the flow structure within the separation bubble (SB), extending the SB length by 30 % over that for SW, and have lingering effects far downstream. Grooves decrease skin friction but increase the bump's form drag by 25 %. In GW, the peaks of turbulence intensity and production decrease by 20 % and shift downstream, compared with SW. Three regions of negative production, found upstream as well as downstream of the bump, are explained in terms of two separate mechanisms: normal and shear productions. Separation upstream of the bump occurs always for GW, but intermittently for SW. Within the downstream SB, counter-rotating minibubbles form intermittently for SW but always for GW. Interestingly, a minibubble causes streamwise vorticity reversal of the upstream moving secondary flow around each crest corner. The wall pressure in GW is invariant in the spanwise direction and is explained in terms of its non-local nature and its connection with outer structures. The grooved bump unearths rich TBL flow physics – upstream separation, dynamics of the downstream minibubble, altered reattachment dynamics and negative production.

In the present study, the flow–structure interaction of a starting jet through a flexible nozzle is experimentally investigated, with a focus on the optimal flexibility for thrust generation. Water slug is impulsively accelerated through a cylindrical nozzle, fabricated with silicone rubber of varying flexibility. In general, the flexible nozzle modifies the vortical structure of the jet and augments the thrust of the starting jet. The measurement of nozzle surface deformation revealed that a back-and-forth wave propagation on the nozzle surface is responsible for the jet-vortex evolution augmenting the thrust generation. Combining the hydrodynamic conservation equations and the linearized shell theory, we also formulated the governing equations, dominated by two relevant dimensionless parameters: the effective acceleration time of the jet ($\varPi _0$) and the effective nozzle stiffness ($\varPi _1$). Asymptotic analysis of the equation showed that the dimensionless wave speed ($\hat {c}$) is expressed as $\hat {c}=(\varPi _{0}^{2}\varPi _{1}/2)^{0.5}$, and the jet momentum is maximized at $\hat {c}=\hat {c}_{crit}$ ($\simeq 3.0$), the condition at which the release of elastic energy stored during nozzle contraction to the jet is synchronized with the instant of termination of jet acceleration. While $\hat {c}=\hat {c}_{crit}$, the achievable maximum jet velocity decreases with the effective acceleration time of the jet ($\varPi _0$), which is attributed to the reduced speed of the surface wave by the flow inside the nozzle.

An increased number of rogue waves, relative to standard distributions, can be induced by unidirectional waves passing over abrupt decreases in water depth. We investigate this phenomenon in a more general setting of multidirectional waves. We examine the influence of the directionality on the occurrence probability of rogue waves using laboratory experiments and fully nonlinear potential flow simulations. Based on the analysis of the statistics of random waves, we find that directional spreading reduces the formation probability of rogue waves relative to unidirectional seas. Nevertheless, for typical values of directional spreading in the ocean ($15^{\circ }\unicode{x2013}30^{\circ }$), our numerical results suggest that there is still a significant enhancement to the number of rogue waves just beyond the top of a depth discontinuity.

Shock buffet on wings is a phenomenon caused by strong shock-wave/boundary-layer interaction resulting first in self-sustained flow unsteadiness and eventually in a detrimental structural response called buffeting. While it is an important aspect of wing design and aircraft certification, particularly for modern transonic air transport, not all of the underlying multidisciplinary physics is thoroughly understood. Building upon a single-discipline shock-buffet stability study, this work now investigates the impact of an elastic structure in these extreme flow conditions. Specifically, a triglobal stability analysis of a fluid–structure coupled system is presented, utilising the implicitly restarted Arnoldi method with a sparse iterative Krylov solver and novel preconditioner. Asymmetry resulting from a static aeroelastic simulation based on a finite-element model of the underlying geometry in a wind tunnel modifies the global modes of the earlier fluid-only symmetric full-span analysis. A flutter stability analysis at wind-tunnel flow conditions below shock-buffet onset finds no instability in the structural degrees-of-freedom, whereas in shock-buffet flow with globally unstable fluid modes additional marginally unstable structural (and fluid) modes emerge. The developed stability tool for coupled analysis is instrumental in identifying those physically relevant and strongly coupled modes where a standard pk-type (p being eigenvalue and k reduced frequency) flutter analysis fails. With the complementary computation of adjoint eigenmodes, the core of the instability is pinpointed to a relatively small wing area which may help to effect the control and delay of this detrimental transonic unsteadiness. We contribute to the question on how the presence of the elastic wing structure impacts on the otherwise pure aerodynamic three-dimensional shock-buffet dynamics.

When a liquid slams into a solid, the intermediate gas is squeezed out at a speed that diverges when approaching the moment of impact. Although there is mounting experimental evidence that instabilities form on the liquid interface during such an event, understanding of the nature of these instabilities is limited. This study therefore addresses the stability of a liquid–gas interface with surface tension, subject to a diverging flow in the gas phase, where the liquid and the gas phase are both represented as potential fluids. We perform a Kelvin–Helmholtz-type linear modal stability analysis of the surface to obtain an amplitude equation that is subsequently analysed in detail and applied to two cases of interest for impact problems, namely, the parallel impact of a wave onto a vertical wall, and the impact of a horizontal plate onto a liquid surface. In both cases we find that long wavelengths are stabilised considerably in comparison with what may be expected based upon classical knowledge of the stability of interfaces subject to a constant gas flow. In the former case, this leads to the prediction of a marginally stable wavelength that is completely absent in the classical analysis. For the latter we find much resemblance to the classical case, with the connotation that the instability is suppressed for smaller disk sizes. The study ends with a discussion of the influence of gas viscosity and gas compressibility on the respective stability diagrams.

The statistical characteristics and the evolution of the backflow structures are investigated in wall-bounded flows at Reynolds numbers up to $Re_{\tau }=1000$. The backflow is caused by the joining of large-scale high- and low-speed structures in the vicinity of the wall and is formed at the tail tip of the low-speed structure. The distribution density of the backflow structures and the percentage area of the backflow region on the wall both increase with the Reynolds number. The backflow structures have an average lifespan of 8 wall units which is found to be slightly longer in the pipe than the channel, and they are convected downstream at the average velocities of the buffer region of approximately 10 wall units, similar to Cardesa et al. (J. Fluid Mech., vol. 880, 2019, R3). The backflow structures occasionally split and merge, and can form detached from the wall. Evidence shows that the split, merged and wall-detached backflow structures are caused by the near-wall structures. The split backflow structures are on average, larger and more spanwise-elongated which are split due to the spanwise shearing of the near-wall streaks. A backflow structure is formed detached from the wall when the trailing end of its carrier low-speed structure ‘sits’ on the near-wall high-speed streaks. The wall-detached backflow structures tend to become wall-attached by approaching the wall when undergoing a similar life cycle to the normal backflow of growth and decay with spanwise elongation because the backflow region at the tail of the low-speed structure is continuously pressed down to the wall by the high-speed structure driven by persistent vortical structures in the buffer region.

A light breeze rising over calm water initiates an intricate chain of events that culminates in a centimetres-deep turbulent shear layer capped by gravity–capillary ripples. At first, viscous stress accelerates a laminar wind-drift layer until small surface ripples appear. The surface ripples then catalyse the growth of a second instability in the wind-drift layer, which eventually sharpens into along-wind jets and downwelling plumes, before devolving into three-dimensional turbulence. In this paper, we compare laboratory experiments with simplified, wave-averaged numerical simulations of wind-drift layer evolution beneath monochromatic, constant-amplitude surface ripples seeded with random initial perturbations. Despite their simplicity, our simulations reproduce many aspects of the laboratory-based observations – including the growth, nonlinear development and turbulent breakdown the wave-catalysed instability – generally validating our wave-averaged model. But we also find that the simulated development of the wind-drift layer is disturbingly sensitive to the amplitude of the prescribed surface wave field, such that agreement is achieved through suspiciously careful tuning of the ripple amplitude. As a result of this sensitivity, we conclude that wave-averaged models should really describe the coupled evolution of the surface waves together with the flow beneath to be regarded as truly ‘predictive’.

The main objective of this work is to develop a unified framework that can be used as a lens to quantitatively assess and augment a wide range of coarse-grained models of turbulence, namely large eddy simulations (LES), hybrid Reynolds-averaged/LES methods and wall-modelled (WM)LES. Taking a turbulent channel flow as an example, optimality is assessed in the wall-resolved limit, the hybrid RANS–LES limit and the WMLES limit, via projections at different resolutions suitable for these approaches. These optimal a priori estimates are shown to have similar characteristics to existing a posteriori solutions reported in the literature. Consistent accuracy metrics are developed for scale-resolving methods using the optimal solution as a reference, and evaluations are performed. We further characterise the slip velocity in WMLES in terms of the near-wall under-resolution and develop a universal scaling relationship. Insights from the a priori tests are used to augment existing slip-based wall models. Various a posteriori tests reveal superior performance over the dynamic slip wall model. Guidance for the development of improved slip-wall models is provided, including a target for the dynamic procedure.

Particle-resolved direct numerical simulations are employed to investigate the particle–particle drag force in the bidisperse gas–particle suspensions where the particles are smooth and the single-particle velocity distribution function is Maxwellian. The particle Reynolds number ranges from 6.7 to 123.8, and in this range the particle inertia is high enough that the lubrication force is not essential. It is found that the relation derived by the kinetic theory of granular flow (KTGF) highly overestimates the particle–particle drag force. This is because the pre-collision velocities of colliding particles are not completely uncorrelated with each other. From the time sequence of collision events, it is observed that the particle pair that has just collided will probably collide again after a short time due to the restriction of the particle motion in dense suspensions. Since the post-collision velocities of the first collision cannot relax entirely in such a short time, the relative velocity before the subsequent collision is statistically smaller than the domain-averaged relative velocity. Consequently, the particle–particle drag force is over-predicted when the domain-averaged relative velocity is used. For this reason, this work assumes that the particle–particle drag force is determined by the relative velocity within a local region near large particles. When the local region is set to be the spherical shells centred on the centres of large particles and with an outer radius of a mean free path of small particles, the KTGF-based relation can reasonably predict the particle–particle drag force.

Taylor's hypothesis, or the frozen turbulence approximation, can be used to estimate also the specific energy dissipation rate 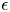$\epsilon$ by comparing experimental results with the Kolmogorov–Obukhov expression. The hypothesis assumes that a frequency detected by an instrument moving with a constant large velocity 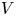$V$ can be related to a wavenumber by 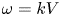$\omega = k V$. It is, however, not obvious how large the translational velocity has to be in order to make the hypothesis valid, or at least applicable with some acceptable uncertainty. Using the space–time-varying structure function for homogeneous and isotropic conditions, this question is addressed in the present study with emphasis on small velocities 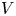$V$. The structure function is obtained using results from numerical solutions of the Navier–Stokes equation. Particular attention is given to the 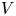$V$ variation of the estimated specific energy dissipation, 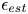$\epsilon _{est}$, compared with the actual value, 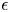$\epsilon$, used in the numerical calculations. In contrast to previous studies, the results emphasize velocities 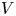$V$ less than or comparable to the one-component root-mean-square velocity, 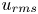$u_{rms}$. We find that 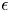$\epsilon$ can be determined to an acceptable accuracy for 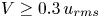$V \geq 0.3\,u_{rms}$. A simple analytical model is suggested to explain the main features of the observations, both Eulerian and Lagrangian. The model assumes that the observed time variations are solely due to eddies moving past the observer, thus ignoring eddy deformation and intermittency effects. In spite of these simplifications, the analysis accounts for most of the numerical results when also eddy-size-dependent velocities are accounted for.

The local streamline topology classification method of Chong et al. (Phys. Fluids A: Fluid Dyn., vol. 2, no. 5, 1990, pp. 765–777) is adapted and extended to describe the geometry of infinitesimal vortex lines. Direct numerical simulation (DNS) data of forced isotropic turbulence reveals that the joint probability density function (p.d.f.) of the second ($q_\omega$) and third ($r_\omega$) normalized invariants of the vorticity gradient tensor asymptotes to a self-similar bell shape for $Re_\lambda > 200$. The same p.d.f. shape is also seen at the late stages of breakdown of a Taylor–Green vortex suggesting the universality of the bell-shaped p.d.f. form in turbulent flows. Additionally, vortex reconnection from different initial configurations is examined. The local topology and geometry of the reconnection bridge is shown to be nearly identical in all cases considered in this work. Overall, topological characterization of the vorticity field provides a useful analytical basis for examining vorticity dynamics in turbulence and other fluid flows.

Lagrangian averaging plays an important role in the analysis of wave–mean-flow interactions and other multiscale fluid phenomena. The numerical computation of Lagrangian means, e.g. from simulation data, is, however, challenging. Typical implementations require tracking a large number of particles to construct Lagrangian time series, which are then averaged using a low-pass filter. This has drawbacks that include large memory demands, particle clustering and complications of parallelisation. We develop a novel approach in which the Lagrangian means of various fields (including particle positions) are computed by solving partial differential equations (PDEs) that are integrated over successive averaging time intervals. We propose two strategies, distinguished by their spatial independent variables. The first, which generalises the algorithm of Kafiabad (J. Fluid Mech., vol. 940, 2022, A2), uses end-of-interval particle positions; the second uses directly the Lagrangian mean positions. The PDEs can be discretised in a variety of ways, e.g. using the same discretisation as that employed for the governing dynamical equations, and solved on-the-fly to minimise the memory footprint. We illustrate the new approach with a pseudo-spectral implementation for the rotating shallow-water model. Two applications to flows that combine vortical turbulence and Poincaré waves demonstrate the superiority of Lagrangian averaging over Eulerian averaging for wave–vortex separation.

An experiment on convective flows induced by the dielectrophoretic force was performed under the microgravity condition provided during a sounding rocket flight. The dielectrophoretic force possesses a non-conservative term that can be seen as resulting from an electric gravity. That gravity can be responsible for an electric Rayleigh–Bénard convection between a hot inner cylinder and a cold outer cylinder when an electric field is applied in the radial direction. Four cells with independent temperature and electric field controls allowed the investigation of eight different values of the electric Rayleigh number relatively close to the onset of the thermo-electric instability. A linear stability analysis is performed to predict the stability threshold and the evolution of the growth rate of the instability. The three-dimensional structure of the flow is captured by simultaneous particle image velocimetry and by shadowgraphy. The amplitude of the instability modes and the time evolution of the flow is analysed, and various methods are proposed to extrapolate the experimental critical value of the electric Rayleigh number for the onset of convection. The measured critical electric Rayleigh number is in agreement with the prediction of the linear stability theory. The comparison of the new experimental results with previous ones from parabolic flight campaigns highlights the importance of long-term microgravity for the achievement of thermal convection at low values of the control parameters.

Fast agglomeration by emulsion binders to capture fine, hydrophobic particles has been developed in the past few years as an alternative to froth flotation by small air bubbles. This new method consists of mixing a particle suspension and saltwater-filled droplets covered with semi-permeable oil layers. These droplets expand due to an osmotic flux of water caused by the presence of salt inside the droplets. To better understand the physics underlying this novel particle capture method, we investigate binary interactions between droplets and particles. The current work examines the dynamics of a rigid spherical particle and a semi-permeable spherical drop that expands due to osmosis in an external, pure-extensional flow field. The droplet is governed by an expansion-diffusion problem, which is coupled to the set of dynamical equations governing the relative particle trajectory. By performing multiple trajectory simulations, we calculate transient collision efficiencies, which can be used to determine the collision kernel for population dynamics. We also use these simulations to better understand the evolution of the microstructure by determining the transient behaviour of the pair distribution function. Our results indicate that the presence of drop expansion increases the collision efficiency of the system, especially for very small particles, which are the most difficult to capture by froth flotation. Moreover, although the presence of slow salt diffusion inside the drops can mitigate this improvement, the contribution of expansion to the collision efficiency may still be considerable, even in the absence of hydrophobic or other attractive forces.