Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-09T18:25:18.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition to turbulence in wind-drift layers

Published online by Cambridge University Press:  24 November 2023

Gregory LeClaire Wagner Open the ORCID record for Gregory LeClaire Wagner [Opens in a new window] ,
Nick Pizzo Open the ORCID record for Nick Pizzo [Opens in a new window] ,
Luc Lenain Open the ORCID record for Luc Lenain [Opens in a new window]  and
Fabrice Veron Open the ORCID record for Fabrice Veron [Opens in a new window]
Gregory LeClaire Wagner*
Affiliation:
Department of Earth, Atmosphere, and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Nick Pizzo
Affiliation:
Graduate School of Oceanography, University of Rhode Island, Narragansett, RI 02882, USA Scripps Institution of Oceanography, University of California, San Diego, La Jolla, CA 92037, USA
Luc Lenain
Affiliation:
Scripps Institution of Oceanography, University of California, San Diego, La Jolla, CA 92037, USA
Fabrice Veron
Affiliation:
School of Marine Science and Policy, University of Delaware, Newark, DE 19716, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

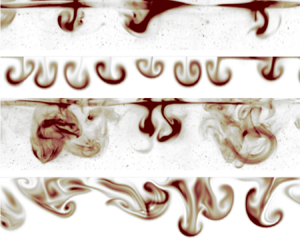
A light breeze rising over calm water initiates an intricate chain of events that culminates in a centimetres-deep turbulent shear layer capped by gravity–capillary ripples. At first, viscous stress accelerates a laminar wind-drift layer until small surface ripples appear. The surface ripples then catalyse the growth of a second instability in the wind-drift layer, which eventually sharpens into along-wind jets and downwelling plumes, before devolving into three-dimensional turbulence. In this paper, we compare laboratory experiments with simplified, wave-averaged numerical simulations of wind-drift layer evolution beneath monochromatic, constant-amplitude surface ripples seeded with random initial perturbations. Despite their simplicity, our simulations reproduce many aspects of the laboratory-based observations – including the growth, nonlinear development and turbulent breakdown the wave-catalysed instability – generally validating our wave-averaged model. But we also find that the simulated development of the wind-drift layer is disturbingly sensitive to the amplitude of the prescribed surface wave field, such that agreement is achieved through suspiciously careful tuning of the ripple amplitude. As a result of this sensitivity, we conclude that wave-averaged models should really describe the coupled evolution of the surface waves together with the flow beneath to be regarded as truly ‘predictive’.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Turbulent Flows: Wave-turbulence interactions Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 976 , 10 December 2023 , A8
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Buckley, M.P. & Veron, F. 2017 Airflow measurements at a wavy air–water interface using PIV and LIF. Exp. Fluids 58 (11), 161.CrossRefGoogle Scholar
Constantinou, N.C. 2015 Formation of large-scale structures by turbulence in rotating planets. PhD thesis, National and Kapodistrian University of Athens, Athens.Google Scholar
Craik, A.D.D. & Leibovich, S. 1976 A rational model for Langmuir circulations. J. Fluid Mech. 73 (3), 401–426.CrossRefGoogle Scholar
D'Asaro, E.A., Thomson, J., Shcherbina, A.Y., Harcourt, R.R., Cronin, M.F., Hemer, M.A. & Fox-Kemper, B. 2014 Quantifying upper ocean turbulence driven by surface waves. Geophys. Res. Lett. 41 (1), 102–107.CrossRefGoogle Scholar
Handler, R.A., Smith, G.B. & Leighton, R.I. 2001 The thermal structure of an air–water interface at low wind speeds. Tellus A 53 (2), 233–244.CrossRefGoogle Scholar
Harcourt, R.R. 2015 An improved second-moment closure model of Langmuir turbulence. J. Phys. Oceanogr. 45 (1), 84–103.CrossRefGoogle Scholar
Jessup, A.T., Zappa, C.J. & Yeh, H. 1997 Defining and quantifying microscale wave breaking with infrared imagery. J. Geophys. Res.: Oceans 102 (C10), 23145–23153.CrossRefGoogle Scholar
Melville, W.K., Shear, R. & Veron, F. 1998 Laboratory measurements of the generation and evolution of Langmuir circulations. J. Fluid Mech. 364, 31–58.CrossRefGoogle Scholar
Ramadhan, A., Wagner, G., Hill, C., Campin, J.-M., Churavy, V., Besard, T., Souza, A., Edelman, A., Ferrari, R. & Marshall, J. 2020 Oceananigans. jl: fast and friendly geophysical fluid dynamics on GPUS. J. Open Source Softw. 5 (53).CrossRefGoogle Scholar
Reichl, B.G. & Li, Q. 2019 A parameterization with a constrained potential energy conversion rate of vertical mixing due to langmuir turbulence. J. Phys. Oceanogr. 49 (11), 2935–2959.CrossRefGoogle Scholar
Sullivan, P.P. & McWilliams, J.C. 2010 Dynamics of winds and currents coupled to surface waves. Annu. Rev. Fluid Mech. 42, 19–42.CrossRefGoogle Scholar
Sutherland, P. & Melville, W.K. 2013 Field measurements and scaling of ocean surface wave-breaking statistics. Geophys. Res. Lett. 40 (12), 3074–3079.CrossRefGoogle Scholar
Thorpe, S.A. 2004 Langmuir circulation. Annu. Rev. Fluid Mech. 36, 55–79.CrossRefGoogle Scholar
Vanneste, J. & Young, W.R. 2022 Stokes drift and its discontents. Phil. Trans. R. Soc. A 380 (2225), 20210032.CrossRefGoogle ScholarPubMed
Veron, F. & Melville, W.K. 1999 Pulse-to-pulse coherent doppler measurements of waves and turbulence. J. Atmos. Ocean. Technol. 16 (11), 1580–1597.2.0.CO;2>CrossRefGoogle Scholar
Veron, F. & Melville, W.K. 2001 Experiments on the stability and transition of wind-driven water surfaces. J. Fluid Mech. 446, 25–65.CrossRefGoogle Scholar
Veron, F., Melville, W.K. & Lenain, L. 2008 Wave-coherent air–sea heat flux. J. Phys. Oceanogr. 38 (4), 788–802.CrossRefGoogle Scholar
Wagner, G.L., Chini, G.P., Ramadhan, A., Gallet, B. & Ferrari, R. 2021 Near-inertial waves and turbulence driven by the growth of swell. J. Phys. Oceanogr. 51 (5), 1337–1351.CrossRefGoogle Scholar
Zappa, C.J., Asher, W.E. & Jessup, A.T. 2001 Microscale wave breaking and air-water gas transfer. J. Geophys. Res.: Oceans 106 (C5), 9385–9391.CrossRefGoogle Scholar