Predicting the performance of large turbine arrays requires the understanding of many physical factors, such as array geometry, turbine operation, inflow conditions and turbulent wake mixing. Due to the large parameter space that an array may be optimised over, low-order models with low computational cost are often employed. This paper extends one of these models, the inviscid–viscous coupled model, for multi-row turbine modelling. Firstly, an extension to the inviscid actuator disc theory is presented by removing the limit on the number of discrete streamtubes computed. The extended model allows for the quantification of the impact of shear in the bypass and core flows separately. In particular, it is shown that averaging a sheared bypass flow profile can result in a substantial over-prediction of the power of a turbine in a laterally bounded flow as the effective blockage of the flow increases. The model is also used to confirm that an approximation using a limited number of streamtubes in some previous applications of the inviscid–viscous approach has a negligible impact on the results. Secondly, we explore the performance of a multi-row array with either uniform or varying turbine resistance across different rows. Results suggest that by varying resistance across rows, the array may outperform the uniform resistance case. The performance gain is dependent, however, on the arrangement and inter-turbine spacing both in the spanwise and streamwise directions.

The cubic interactions in a discrete system of four weakly nonlinear waves propagating in a conservative dispersive medium are studied. By reducing the problem to a single ordinary differential equation governing the motion of a classical particle in a quartic potential, the complete explicit branches of solutions are presented, either steady, periodic, breather or pump, thus recovering or generalizing some already published results in hydrodynamics, nonlinear optics and plasma physics, and presenting some new ones. Various stability criteria are also formulated for steady equilibria. Theory is applied to deep-water gravity waves for which models of isolated quartets are described, including bidirectional standing waves and quadri-directional travelling waves, steady or not, resonant or not.

Understanding and controlling fluid entrapment during forced imbibition in porous media is crucial for many natural and industrial applications. However, the microscale physics and macroscopic consequences of fluid entrapment in these geometric-confined porous media remain poorly understood. Here, we introduce a novel multidepth microfluidic chip, which can mitigate the depth confinement of traditional two-dimensional (2-D) microfluidic chips and mimic the wide pore size distribution as natural-occurring three-dimensional (3-D) porous media. Based on microfluidic experiments and direct numerical simulations, we observe the fluid-entrapment scenarios and elucidate the underlying complex interaction between geometric confinement, capillary number and wettability. Increasing depth variation can promote fluid entrapment, whereas increasing capillary number and contact angle yield the opposite effect, which seemingly contradicts conventional expectations in traditional 2-D microfluidic chips. The fluid-entrapment scenario in depth-variable microfluidic chips stems from microscopic interfacial phenomena, classified as snap-off and bypass events. We provide theoretical analyses of these pore-scale events and validate corresponding phase diagrams numerically. It is shown that increasing depth variation triggers snap-off and bypass events. Conversely, a higher capillary number suppresses snap-off events under strong imbibition, and an increased contact angle inhibits bypass events under imbibition. These macroscopic imbibition patterns in microfluidic porous media can be linked with these pore-scale events by improved dynamic pore-network models. Our findings bridge the understanding of forced imbibition between 2-D and 3-D porous media and provide design principles for newly engineered porous media with respect to their desired imbibition behaviours.

We study the effects of buoyancy, surface-tension gradients and phase boundary on the stability of a layer of water that is confined between air at the top and a layer of ice at the bottom. The temperature of the overlying air and flux condition at the free surface of the water layer are such that the layer is susceptible to both thermal and thermocapillary instabilities. We perform a linear stability analysis to identify these modes of instability and investigate the effects of the phase boundary on them. We find that with increasing thickness of the ice layer, the critical Rayleigh and Marangoni numbers for the instabilities are found to first decrease and then asymptote to constant values for ice thicknesses much larger than the thickness of the water layer. In the case of thermocapillary instability, we find that the thickness of the ice layer has negligible influence on the stability threshold for dimensionless wavenumber $k \gg 1$, and that the presence of an unstably stratified liquid layer significantly alters the stability threshold for $k = O (1)$. Furthermore, the inclusion of Marangoni stresses reduces the stability threshold of the thermal instability.

The Rayleigh–Taylor instability at the interface of two sheared fluid layers in a horizontal channel is investigated in the absence of inertia. The dynamics of the flow is described by a nonlinear lubrication equation which is solved numerically for adverse density stratifications. The early-time dynamics features a number of finger-like protrusions of different heights at the interface. The fingers travel at different speeds leading to a sequence of merging events after which the interface eventually settles to a near-saturated state, comprising only one finger that includes most of the lower fluid. For sufficiently large density stratifications, the final state spans the height of the channel and includes two thin fluid films at each wall, both of which undergo chaotic dynamics, but finite-time touch-down/touch-up is shown to be precluded by the shear flow. An asymptotic analysis in the large-Bond-number limit (intense density stratification) reveals the finer structure of the final state including Landau–Levich-type connection regions. The asymptotic solutions are compared with numerical results of the lubrication model as well as direct numerical simulations, and excellent agreement is observed between the three in terms of interfacial structure, wave speed and film thicknesses.

A long-wave asymptotic model is developed for the flow of an axisymmetric viscous film lining the interior of a tube for the case where slip occurs at the tube wall. Both the case of a falling film with a passive air core and that of a film driven up the tube by pressure-driven airflow are considered. The impact of slip on the net liquid volume flux is discussed, and linear stability analysis of the evolution equation is conducted to identify the impact of slip on the phase speed and growth rates of disturbances in each case. The presence of slip enhances the growth rates, though its impact on phase speed depends on the film thickness and the strength of the core airflow. For some parameter combinations, slip can modify the phase speed without altering the base flow. The nonlinear evolution of the free surface is then studied numerically. For falling films, increasing the slip length reduces the critical thickness required for plug formation to occur. Families of travelling wave solutions are found via continuation and are used to derive a simple formula for the dependence of this critical thickness on the slip length; this formula is shown to hold for small slip length. For air-driven films, the topology of streamlines in the film can be altered by slip at the wall; if the slip length is large enough, it can prevent regions of recirculation from forming at the wave crest.

Two new flows, a tilted-vortex flow and a periodic-vortex flow, are found numerically at the onset of instability in rotating plane Couette flow (RPCF). It has hitherto been believed that the first few bifurcation sequences from the laminar state are quite well understood, namely, that a streamwise-independent flow with a two-dimensional roll-cell (2dRC) structure bifurcates first, followed by the bifurcation of a wavy-vortex flow (WVF). The present study shows that the 2dRC is, in fact, unstable from its onset, and that the newly found tilted-vortex flow takes over in place of 2dRC. It is further found that the periodic-vortex flow takes part in the early stages of laminar–turbulent transition. The existence of the new flows can be verified by careful examinations of the experimental observations in Hiwatashi et al. (Phys. Fluids, vol. 19, 2007, 048103) and Kawata & Alfredsson (J. Fluid Mech., vol. 791, 2016, 191–213).

We recently lost valuable colleague and friend, Charlie Doering. The following tribute provides an overview of his life.

In this paper, we study non-isochoric models for mixtures of solid particles, at high volume concentration, and a gas. One of the motivations for this work concerns geophysics and more particularly the pyroclastic density currents, whose dense basal parts are precisely mixtures of pyroclasts and lithic fragments and air. They are extremely destructive phenomena, capable of devastating urbanised areas, and are known to propagate over long distances, even over almost flat topography. Fluidisation of these dense granular flows by pore gas pressure is one response that could explain this behaviour and must therefore be taken into account in the models. Starting from a solid–gas mixing model and invoking the compressibility of the gas through a law of state, we rewrite the conservation of mass equation of the gas phase into an equation of the pore gas pressure whose net effect is to reduce the friction between the particles. The momentum equation of the solid phase is completed by generic constitutive laws, specified as in Schaeffer et al. (J. Fluid Mech., vol. 874, 2019, pp. 926–951) by a yield function and a dilatancy function. Therefore, the divergence of the velocity field, which reflects the ability of the granular flow to expand or compress, depends on the volume fraction, pressure, strain rate and inertial number. In addition, we require the dilatancy function to describe the rate of volume change of the granular material near an isochoric equilibrium state, i.e. at constant volume. This property ensures that the volume fraction, which is the solution to the conservation of mass equation, is positive and finite at all times. We also require that the non-isochoric fluidised model be linearly stable and dissipate energy (over time). In this theoretical framework, we derive the dilatancy models corresponding to classical rheologies such as Drucker–Prager and $\mu (I)$ (with or without expansion effects). The main result of this work is to show that it is possible to obtain non-isochoric and fluidised granular models satisfying all the properties necessary to correctly account for the physics of granular flows and which are well posed, at least linearly stable.

We present direct numerical simulation (DNS) and modelling of incompressible, turbulent, generalized Couette–Poiseuille flow. A particular example is specified by spherical coordinates $(Re,\theta,\phi )$, where $Re = 6000$ is a global Reynolds number, $\phi$ denotes the angle between the moving plate, velocity-difference vector and the volume-flow vector and $\tan \theta$ specifies the ratio of the mean volume-flow speed to the plate speed. The limits $\phi \to 0^\circ$ and $\phi \to 90^\circ$ give alignment and orthogonality, respectively, while $\theta \to 0^\circ,\ \theta \to 90^\circ$ correspond respectively to pure Couette flow in the $x$ direction and pure Poiseuille flow at angle $\phi$ to the $x$ axis. Competition between the Couette-flow shear and the forced volume flow produces a mean-velocity profile with directional twist between the confining walls. Resultant mean-speed profiles relative to each wall generally show a log-like region. An empirical flow model is constructed based on component log and log-wake velocity profiles relative to the two walls. This gives predictions of four independent components of shear stress and also mean-velocity profiles as functions of $(Re,\theta,\phi )$. The model captures DNS results including the mean-flow twist. Premultiplied energy spectra are obtained for symmetric flows with $\phi =90^\circ$. With increasing $\theta$, the energy peak gradually moves in the direction of increasing $k_x$ and decreasing $k_z$. Rotation of the energy spectrum produced by the faster moving velocity near the wall is also observed. Rapid weakening of a spike maxima in the Couette-type flow regime indicates attenuation of large-scale roll structures, which is also shown in the $Q$-criterion visualization of a three-dimensional time-averaged flow.

This study examines the two-dimensional interaction of two unequal co-rotating viscous vortices in uniform background shear. Numerical simulations are performed for vortex pairs having various circulation ratios 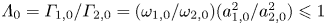$\varLambda _0 = \varGamma _{1,0}/\varGamma _{2,0} = (\omega _{1,0}/\omega _{2,0})(a^2_{1,0}/a^2_{2,0}) \leqslant 1$, corresponding to different initial characteristic radii 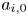$a_{i,0}$ and peak vorticities 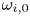$\omega _{i,0}$ of each vortex 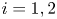$i=1,2$, in shears of various strengths 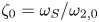$\zeta _0 = \omega _S/\omega _{2,0}$, where 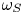$\omega _S$ is the constant vorticity of the shear. Two primary flow regimes are observed: separations (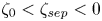$\zeta _0 < \zeta _{sep} < 0$), in which the vortices move apart continuously, and henditions (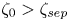$\zeta _0 > \zeta _{sep}$), in which the interaction results in a single vortex (where 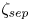$\zeta _{sep}$ is the adverse shear strength beyond which separation occurs). Vortex motion and values of 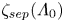$\zeta _{sep}(\varLambda _0)$ are well-predicted by a point-vortex model for unequal vortices. In vortex-dominated henditions, shear varies the peak–peak distance 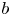$b$, and vortex deformation. The main convective interaction begins when core detrainment of one vortex is established, and proceeds similarly to the no-shear (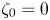$\zeta _0 = 0$) case: merger occurs if the second vortex also detrains, engendering mutual entrainment; otherwise straining out occurs. Detrainment requires persistence of straining of both sufficient magnitude, as indicated by relative straining above a consistent critical value, 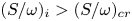$(S/\omega )_i > (S/\omega )_{cr}$, where 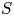$S$ is the strain rate magnitude at the vorticity peak, and conducive direction. Hendition outcomes are assessed in terms of an enhancement factor 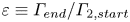$\varepsilon \equiv \varGamma _{end}/\varGamma _{2,start}$. Although 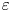$\varepsilon$ generally varies with 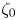$\zeta _0$, 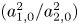$(a^2_{1,0} /a^2_{2,0} )$ and 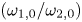$(\omega _{1,0}/\omega _{2,0})$ in a complicated manner, this variation is well-characterized by the pair's starting enstrophy ratio, 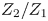$Z_2/Z_1$. Within a transition region between merger and straining out (approximately 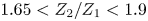$1.65 < Z_2/Z_1 < 1.9$), shear of either sense may increase 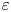$\varepsilon$.

This paper presents the results of the time resolved flow field measurements around a realistic rowing oar blade that moves along a realistic path through water. To the authors’ knowledge no prior account of this complex flow field has been given. Simultaneously with the flow field measurements, the hydrodynamic forces acting on the blade were measured. These combined measurements allow us to identify the relevant flow physics that governs rowing propulsion, and subsequently use this information to adjust the oar blade configuration to improve rowing propulsion. Analysis of the instationary flow field around the oar blade during the drive phase indicated how the initial formation, and subsequent development, of leading-edge and trailing-edge vortices are related to the generation of instationary lift and drag forces, and how these forces contribute to rowing propulsion. It is shown that the observed individual flow mechanisms are similar to the flow mechanisms observed in bird flight, but that the overall propulsive mechanism for rowing propulsion is fundamentally different. To quantify the rowing propulsion efficiency, we introduced the energetic efficiency $\eta _E$ and the impulse efficiency $\eta _J$, where the latter can be interpreted as the alignment of the generated impulse with the propulsive direction. It is found that in the conventional oar blade configuration, the generated impulse is not aligned with the propulsive direction, indicating that the propulsion is suboptimal. By adjusting the angle at which the blade is attached to the oar, the generation of leading- and trailing-edge vortices is altered such that the generated impulse better aligns with the propulsive direction, thus increasing the efficiency.

The instability mechanism behind a geometrically simple cylindrical roughness element continues to be a challenging topic in fluid mechanics. Considerable progress has been made in understanding the phenomena in recent years, but more research is needed to predict the temporal nature and spatial structure of the dominant instability in a given flow configuration. This is of particular interest, as these instabilities dictate the transition to turbulence and thus are significant for large-scale effects such as skin friction drag. A smoke-flow visualization study with a large variation of parameters, featuring a cylindrical roughness element connected to a linear traverse, has been performed. Results show good agreement with previous investigations and provide further insights into the stability properties, revealing several unexpected effects. For a low roughness aspect ratio $\eta$, no global instability is detected even at the highest roughness Reynolds number $Re_{kk}$, whereas a high aspect ratio indicates a delay in the onset of instability. From the acquired visualizations, we constructed the, so far, richest instability diagram of the wake behind an isolated roughness element in the $Re_{kk}\unicode{x2013}\eta$ space, sampled in the same measurement campaign. Furthermore, information regarding the dominant frequency in the wake can be extracted from the visualization images. Our results suggest a new scaling of the frequency as the velocity is increased. Finally, it is shown that the dominant frequency in a certain flow regime can be well predicted using a Strouhal number based on the cylinder diameter and the roughness velocity.

The nonlinear robustness of laminar plane Couette flow is considered under the action of in-phase spanwise wall oscillations by computing properties of the edge of chaos, i.e. the boundary of its basins of attraction. Three measures are used to quantify the chosen control strategy on laminar-to-turbulent transition: the kinetic energy of edge states (local attractors on the edge of chaos), the form of the minimal seed (least energetic perturbation on the edge of chaos), and the laminarization probability (the probability that a random perturbation from the laminar flow of given kinetic energy will laminarize). A novel Bayesian approach is introduced to enable the accurate computation of the laminarization probability at a fraction of the cost of previous methods. While the edge state and the minimal seed provide useful information about the dynamics of transition to turbulence, neither measure is particularly useful to judge the effectiveness of the control strategy since they are not representative of the global geometry of the edge. In contrast, the laminarization probability provides global information about the edge and can be used to evaluate the control effectiveness by computing a laminarization score (the expected laminarization probability) and the associated expected dissipation rate of the controlled flow. These two quantities allow for the determination of optimal control parameter values subject to desired constraints. The results discussed in the paper are expected to be applied to a wide range of transitional flows and control strategies aimed at suppressing or triggering transition to turbulence.

The topology of turbulent coherent structures is known to regulate the transport of energy, mass and momentum in the atmospheric boundary layer (ABL). While previous research has primarily focused on characterizing the structure of turbulence in stationary ABL flows, real-world scenarios frequently deviate from stationarity, giving rise to nuanced and poorly understood changes in the turbulence geometry and associated transport mechanisms. This study sheds light on this problem by examining topological changes in ABL turbulence induced by non-stationarity and their effects on momentum transport. Results from a large-eddy simulation of pulsatile open channel flow over an array of surface-mounted cuboids are examined. The analysis reveals that the flow pulsation triggers a phase-dependent shear rate, and the ejection-sweep pattern varies with the shear rate during the pulsatile cycle. From a turbulence structure perspective, it is attributed to the changes in the geometry of hairpin vortices. An increase (decrease) in the shear rate intensifies (relaxes) these structures, leading to an increase (decrease) in the frequency of ejections and an amplification (reduction) of their percentage contribution to the total momentum flux. Furthermore, the size of the hairpin packets undergoes variations, which depend on the geometry of the constituting hairpin vortices, yet the packet inclination preserves its orientation throughout the pulsatile cycle. These observations reinforce the important role non-stationarity holds in shaping the structure of ABL turbulence and the momentum transport mechanisms it governs.

Previous analyses of the flow of low-Reynolds-number, viscous gravity currents down inclined planes are investigated further and extended. Particular emphasis is on the motion of the fluid front and tail, which previous analyses treated somewhat cavalierly. We obtain reliable, approximate, analytic solutions in these regions, the accuracies of which are satisfactorily tested against our numerical evaluations. The solutions show that the flow has several time scales determined by the inclination angle, $\alpha$. At short times, the influence of initial and boundary conditions is important and the flow is governed by both the pressure gradient and the direct action of gravity due to inclination. Later on, the areas where the boundary conditions are important shrink. This fact explains why previous solutions, being inaccurate near the front and the tail, described experimental data with high accuracy. At larger times, of the order of $\alpha ^{-5/2}$, the influence of the pressure gradient may be neglected and the fluid profile converges to the square-root shape predicted in previous works. Important extensions of our approach are also outlined.

In the present study, the influence of a uniformly moving impinging shock on the resulting shock wave–turbulent boundary layer interaction is numerically investigated. The relative Mach number of the shock front travelling above a flat-plate model varied between 0 and 2.3, while the quasi-steady inflow conditions remained constant with a Mach number of 3. To quantitatively evaluate the effect of shock travelling speed, a well-known scaling method for interaction length in quasi-steady flows was applied as a reference after significant improvements in modelling the effects of Reynolds number and wall temperature using new and existing data. Moreover, previously obtained experimental results for a limited range of travelling speeds were employed to validate the obtained numerical results. Three ranges of shock travelling speeds with distinctly different properties were extracted and quantitatively described using a developed correlation-based approach built on the extended quasi-stationary scaling law. In the first range, the scaled interaction length reaches its maximum for the given interaction strength and can be directly described by the scaling law obtained for quasi-stationary interactions. In the second travelling-speed range, the dependence of the interaction length on the interaction strength is explicitly influenced by the shock movement. With increasing shock travelling speed, the scaled interaction length here decreases significantly faster than in the quasi-stationary reference case. The end of this speed range is reached when the absolute shock front speed has caught up with the maximum speed of sound in the interaction zone, and thus the interaction length has fallen to zero. This travelling-speed limit signifies the transition to the third range, where upstream influence is no longer possible.

The instability and dynamics of a vertical oscillatory boundary layer in a container filled with a stratified fluid are addressed. Past experiments have shown that when the boundary oscillation frequency is of the same order as the buoyancy frequency, the system is unstable to a herringbone pattern of oblique waves. Prior studies assuming the basic state to be a unidirectional oscillatory shear flow were unable to account for the oblique waves. By accounting for confinement effects present in the experiments, and the ensuing three-dimensional structure of the basic state, we are able to numerically reproduce the experimental observations, opening the door to fully analysing the impacts of stratification on such boundary layers.

We study experimentally the aeroelastic instability boundaries and three-dimensional vortex dynamics of pitching swept wings, with the sweep angle ranging from 0$^\circ$ to 25$^\circ$. The structural dynamics of the wings are simulated using a cyber-physical control system. With a constant flow speed, a prescribed high inertia and a small structural damping, we show that the system undergoes a subcritical Hopf bifurcation to large-amplitude limit-cycle oscillations (LCOs) for all the sweep angles. The onset of LCOs depends largely on the static characteristics of the wing. The saddle-node point is found to change non-monotonically with the sweep angle, which we attribute to the non-monotonic power transfer between the ambient fluid and the elastic mount. An optimal sweep angle is observed to enhance the power extraction performance and thus promote LCOs and destabilize the aeroelastic system. The frequency response of the system reveals a structural-hydrodynamic oscillation mode for wings with relatively high sweep angles. Force, moment and three-dimensional flow structures measured using multi-layer stereoscopic particle image velocimetry are analysed to explain the differences in power extraction for different swept wings. Finally, we employ a physics-based force and moment partitioning method to correlate quantitatively the three-dimensional vortex dynamics with the resultant unsteady aerodynamic moment.