We generalise the classical Benjamin solution (Benjamin, J. Fluid Mech., vol. 31, 1968, pp. 209–248) modelling the flow in a horizontal duct of finite depth in situations where the flow contains a region spanning the depth of the duct, and a region in which the surface detaches from the ceiling of the duct as a free surface. It is shown that the Benjamin solution belongs to a one-parameter family of similar solutions, which are divided into two types: solutions that describe potential flows where the free surface of the fluid is deflected from the duct ceiling at a zero angle; and solutions that admit the formation of a vortex flow region in the vicinity of the point of fluid separation from the duct ceiling. It is shown that this one-parameter family of solutions is the limit of a two-parameter family of solutions in which part of the uniform flow energy is converted into energy of the small-scale fluid motion. Based on the local hydrostatic approximation, the applicability of the constructed solutions is discussed.

Solvent exchange is a process involving mixing between a good solvent with dissolved solute and a poor solvent. The process creates local oversaturation which causes the nucleation of minute solute droplets. Such ternary systems on a macro-scale have remained unexplored in the turbulent regime. We experimentally study the solvent exchange process by injecting mixtures of ethanol and trans-anethole into water, forming a turbulent buoyant jet in the upward direction. Locally, turbulent mixing causes oversaturation of the trans-anethole following turbulent entrainment. We optically measure the concentration of the nucleated droplets using a light attenuation technique and find that the radial concentration profile has a sub-Gaussian kurtosis. In contrast to the entrainment-based models, the spatial evolution of the oversaturation reveals continuous droplet nucleation downstream and radially across the jet, which we attribute to the limited mixing capacity of the jet. Although we are far from a full quantitative understanding, this work extends the knowledge on solvent exchange into the turbulent regime, and brings in a novel type of flow, broadening the scope of multicomponent, multiphase turbulent jets with phase transition.

We consider a slowly condensing droplet levitating near the surface of an evaporating layer, and develop a mathematical model to describe diffusion, heat transfer and fluid flow in the system. The method of separation of variables in bipolar coordinates is used to obtain the series expansions for temperature, vapour concentration and the Stokes stream function. This framework allows us to determine temperature profiles and condensation rates at the surface of the droplet, and to calculate the upward force that allows the droplet to levitate. Somewhat counter-intuitively, condensation is found to be the strongest near the bottom of the droplet, which faces the hot liquid layer. The experimentally observed deviations from the classical law predicting the square of the radius to grow linearly in time are explained by the model. A spatially non-uniform phase change rate results in a contribution to the force not considered in previous studies, and comparable to droplet weight and the upward force calculated from the Stokes drag law. The levitation conditions are formulated accordingly, resulting in the prediction of levitation height as a function of droplet size without any fitting parameters. A simple criterion is formulated to define the parameter ranges in which levitation is possible. The results are in good agreement with the experimental data except that the model tends to slightly underpredict the levitation height.

Iceberg melting is a critical factor for climate change. However, the shape of an iceberg is an often neglected aspect of its melting process. Our study investigates the influence of different ice shapes and ambient flow velocities on melt rates by conducting direct numerical simulations of a simplified system of bluff body flow. Our study focuses on the ellipsoidal shape, with the aspect ratio as the control parameter. We found the shape plays a crucial role in the melting process, resulting in significant variations in the melt rate between different shapes. Without flow, the optimal shape for a minimal melt rate is the disk (two-dimensional) or sphere (three-dimensional), due to the minimal surface area. However, as the ambient flow velocity increases, the optimal shape changes with the aspect ratio. We find that ice with an elliptical shape (when the long axis is aligned with the flow direction) can melt up to 10 % slower than a circular shape when exposed to flowing water. Following the approach considered by Huang et al. (J. Fluid Mech., vol. 765, 2015, R3) for dissolving bodies, we provide a quantitative theoretical explanation for this optimal shape, based on the combined contributions from both surface-area effects and convective-heat-transfer effects. Our findings provide insight into the interplay between phase transitions and ambient flows, contributing to our understanding of the iceberg melting process and highlighting the need to consider the aspect-ratio effect in estimates of iceberg melt rates.

Low Stokes number particles at dilute concentrations in turbulent flows can reasonably be approximated as passive scalars. The added presence of a drift velocity due to buoyancy or gravity when considering the transport of such passive scalars can reduce the turbulent dispersion of the scalar via a diminution of the eddy diffusivity. In this work, we propose a model to describe this decay and use a recently developed technique to accurately and efficiently measure the eddy diffusivity using Eulerian fields and quantities. We then show a correspondence between this method and standard Lagrangian definitions of diffusivity and collect data across a range of drift velocities and Reynolds numbers. The proposed model agrees with data from these direct numerical simulations, offers some improvement to previous models in describing other computational and experimental data and satisfies theoretical constraints that are independent of Reynolds number.

Buoyancy-driven turbulent convection leads to a fully compressible flow with a prominent top-down asymmetry of first- and second-order statistics when the adiabatic equilibrium profiles of temperature, density and pressure change very strongly across the convection layer. The growth of this asymmetry and the formation of an increasingly thicker stabilized sublayer with a slightly negative mean convective heat flux $J_c(z)$ at the top of the convection zone is reported here by a series of highly resolved three-dimensional direct numerical simulations beyond the Oberbeck–Boussinesq and anelastic limits for dimensionless dissipation numbers, $0.1 \le D\le 0.8$, at fixed Rayleigh number $Ra=10^6$ and superadiabaticity $\epsilon =0.1$. The highly stratified compressible convection regime appears for $D > D_{crit}\approx 0.65$, when density fluctuations collapse to those of pressure; it is characterized by an up to nearly 50 % reduced global turbulent heat transfer and a sparse network of focused thin and sheet-like thermal plumes falling through the top sublayer deep into the bulk.

In impermeable media, a hydraulic fracture can continue expanding even without additional fluid injection if its volume exceeds the limiting volume of a hydrostatically loaded radial fracture. This limit depends on the mechanical properties of the surrounding solid and the density contrast between the fluid and the solid. We show that two dimensionless numbers characterize self-sustained fracture growth. The first is a buoyancy factor that compares the total released volume to the volume of a hydrostatically loaded radial fracture to determine whether buoyant growth occurs. The second number is the dimensionless viscosity of a radial fracture when buoyant effects become of order one. Notably, this dimensionless viscosity depends on the rate at which the fluid volume is released, indicating that both the total volume and release history impact self-sustained buoyant growth. We identify six well-defined propagation histories based on these two dimensionless numbers. Their growth evolves between distinct limiting regimes of radial and buoyant propagation, resulting in different fracture shapes. Notably, our findings reveal two growth rates depending on the dominant energy dissipation mechanism (viscous flow versus fracture creation) in the fracture head. For finite values of material toughness, the toughness-dominated limit represents a late-time solution for all fractures in growth rate and head shape (possibly reached only at a very late time). The viscosity-dominated limit can appear at intermediate times. Our three-dimensional simulations confirm the predicted scalings. This contribution highlights the importance of the entire propagation and release history for accurate analysis of buoyant hydraulic fractures.

During the high velocity impact of an object on a solid covered with a thin fluid layer, a lubricated contact exists within the short time in which the liquid is squeezed out from the contact. This is important for e.g. the grip of shoes on wet surfaces. We experimentally study the squeeze flow of such layers and find that the amount of viscous dissipation determines how much fluid remains in the contact after the kinetic energy of the impacting object is absorbed. For impacts with sufficient amount of kinetic energy, it is possible to completely drain a Newtonian or shear thinning fluid from the contact on a short time scale. Viscoelastic liquids, however, cannot be drained by increasing impact velocity, because of the fluids’ elastic tendency to retract back into the contact after rapid squeezing. This explains why the presence of polymeric fluids can lead to extreme slipperiness of surfaces. Furthermore, we show that all our experimental results agree with the predictions given by hydrodynamic theory applied to the fluid flow in the gap.

This study examined the impact of coherent structures on the aerodynamic forces exerted on a NACA0012 aerofoil with angles of attack $7.5^{\circ }$ and $10^{\circ }$, and a chord-based Reynolds number $50\,000$. The study utilized the spectral proper orthogonal decomposition (SPOD) algorithm to identify the coherent structures, and vorticity force analysis to quantify their impact on lift and drag forces. Results showed that at $10^{\circ }$, the zeroth frequency of the first SPOD mode had a significant impact on drag and lift forces due to a large vortex structure that caused a strong flow along the suction side of the aerofoil. The first and second frequencies of the first SPOD mode represented asymmetric vortex pairs and a series of vortex pairs that determined the leading-edge separation, respectively. At $7.5^{\circ }$, the zeroth frequency of the first mode corresponded to an oscillating near-wall stream that followed the reattachment flow pattern, while the first frequency corresponded to a counter-rotating vortex pair that originated where the flow reattaches. Finally, the second frequency of the first mode corresponded to smaller counter-rotating vortex pairs at the shear layer originated near the reattachment point. These findings suggest that coherent structures have a significant impact on aerodynamic forces exerted on aerofoils, and can be identified and quantified using the SPOD algorithm and vorticity force analysis.

The paper studies the statistics of total and static temperature (total $h_t$ and static $h$ enthalpy) in compressible turbulent plane channel flow using direct numerical simulations (DNS) data covering the range of centreline Mach numbers $0.3\lessapprox \bar {M}_{{{CL}}_x} \lessapprox 2.5$ and Huang–Coleman–Bradshaw friction Reynolds numbers $100\lessapprox Re_{\tau ^\star }\lessapprox 1000$. For this class of very-cold-wall flows, the DNS data for correlation coefficients and joint probability density functions (p.d.f.s) show that $h_t'$ is invariably very strongly correlated with the streamwise velocity fluctuation $u'$, in contrast to static temperature (static enthalpy $h'$) whose correlation with $u'$ weakens rapidly with increasing wall distance. We study various correlations and joint p.d.f.s of $h_t'$ and $h'$ in relation to the fluctuating velocity field, including the turbulent Prandtl number $Pr_{{T}}$, and discuss the predictions of Reynolds analogy. The scaling of the mean enthalpy and the fluctuating enthalpy variance and fluxes with respect to inner and outer velocity scales is investigated. The complex behaviour and scaling of different terms in the transport equations for the enthalpy variance and fluxes are discussed.

We develop a theoretical model to study (dense) two-dimensional gravity current flow in a laterally extensive porous medium experiencing leakage through a discrete fissure situated along this boundary at some finite distance from the injection point. Our model, which derives from the depth-averaged mass and buoyancy equations in conjunction with Darcy's law, considers dispersive mixing between the gravity current and the surrounding ambient by allowing two different gravity current phases. Thus do we define a bulk phase consisting of fluid whose density is close to that of the source fluid and a dispersed phase consisting of fluid whose density is close to that of the ambient. We characterize the degree of dispersion by estimating, as a function of time, the buoyancy of the dispersed phase and the separation distance between the bulk nose and the dispersed nose. On this basis, it can be shown that the amount of dispersion depends on the flow conditions upstream of the fissure, the fissure permeability and the vertical and horizontal extents of the fissure. We also show that dispersion is larger when the gravity current propagates along an inclined barrier rather than along a horizontal barrier. Model predictions are fitted against numerical simulations. The simulations in question are performed using COMSOL and consider different inclination angles and fissure and upstream flow conditions. Our study is motivated by processes related to underground $\mathrm {H}_2$ storage e.g. an irrecoverable loss of $\mathrm {H}_2$ when it is injected into the cushion gas saturating an otherwise depleted natural gas reservoir.

Many turbulent flows exhibit time-periodic statistics. These include turbomachinery flows, flows with external harmonic forcing and the wakes of bluff bodies. Many existing techniques for identifying turbulent coherent structures, however, assume the statistics are statistically stationary. In this paper, we leverage cyclostationary analysis, an extension of the statistically stationary framework to processes with periodically varying statistics, to generalize the spectral proper orthogonal decomposition (SPOD) to the cyclostationary case. The resulting properties of the cyclostationary SPOD (CS-SPOD for short) are explored, a theoretical connection between CS-SPOD and the harmonic resolvent analysis is provided, simplifications for the low and high forcing frequency limits are discussed, and an efficient algorithm to compute CS-SPOD with SPOD-like cost is presented. We illustrate the utility of CS-SPOD using two example problems: a modified complex linearized Ginzburg–Landau model and a high-Reynolds-number turbulent jet.

Reconfiguration events in turbulent mixed convection, i.e. the superposition of thermal and forced flow contributions, at the two different Richardson numbers $Ri=1.5$ and $Ri=3.7$ and similar Rayleigh numbers of $Ra \approx 10^8$ are investigated with tomographic particle image velocimetry in combination with local temperature measurements. For both cases, the three-dimensional velocity fields reflect diagonally aligned large-scale circulations (LSC) switching their alignment by rotating their axes around a pivot located at the centre of the LSC, while the temperatures perform a translation movement of the structures in agreement with earlier temperature-based investigations. For the high $Ri$ case, the switching process of the observed spontaneous reconfigurations is induced by a reversing thermal flow contribution while the forced flow contribution is constant. Furthermore, it is shown that a secondary roll structure, which drives the reconfiguration process in Rayleigh–Bénard convection, also exists in mixed convection. However, in the latter, the flow reversals are triggered by different structures which accumulate and release their kinetic energy according to a proper orthogonal decomposition analysis. In contrast, for the low $Ri$ case, the structure formation during continuous reconfigurations is governed by a Taylor- or Görtler-type instability. This means that the forced convection substantially affects the reconfiguration mechanism of these structures. Therefore, the reconfigurations cannot be described by a simple superposition of structures associated with the two flow contributions as for the high $Ri$.

We construct reduced-order models of aeroacoustic sources for single and twin subsonic jets (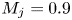$M_j=0.9$, $Re=3600$), with the goal of accurately recovering the far-field sound over a wide band of frequencies 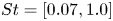$St=[0.07,1.0]$ and directivity angles 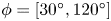$\phi = [30^{\circ },120^{\circ }]$ within a subdecibel level accuracy. These models are realized via combining spatio-temporally coherent spectral proper orthogonal decomposition (SPOD) modes extracted directly from Lighthill's stress tensor, itself calculated using large-eddy simulation (LES). We consider two sets of twin subsonic jets of diameter 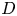$D$ each, with spacings of 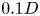$0.1D$ and 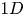$1D$, where the jets merge upstream and downstream of breakdown, respectively. The closely spaced twin jet decays the slowest due to reduced turbulent stresses which are, however, more broadband due to early merging. Such jets show strong shielding in the plane of jets, especially at shallow directivity angles where sound levels may drop below that of the single jet. The farther spaced twin jets have dynamics more akin to the constituent single jet with turbulent fluctuations peaking here at 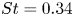$St=0.34$, but showing very little shielding, with their overall sound pressure level (OASPL) mostly linked to the nature of extra flow structures created during merging. Three-dimensional, energy-ranked, coherent structures for twin jets exhibit rather poor low-rank behaviour, especially at the far-field spectral peak 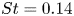$St=0.14$. At 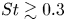$St \gtrsim 0.3$, the SPOD wavepackets show strong visual coherence, resembling Kelvin–Helmholtz instability modes upstream of breakdown, while at the lower frequencies, there is very little spatial coherence with wavepackets peaking downstream of breakdown. Although the leading SPOD modes radiate poorly, reduced-order models using a subset of them, up to 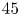$45$ SPOD modes per frequency, show a remarkable match (within 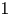$1$ dB) against the LES-predicted sound over 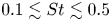$0.1 \lesssim St \lesssim 0.5$, at all angles investigated. At other frequencies, the closely spaced twin jet shows more error, due to its greater hierarchy of spatio-temporal structures, showing slower convergence at the shallower angles.

We provide scaling relations for the Nusselt number $Nu$ and the friction coefficient $C_{S}$ in sheared Rayleigh–Bénard convection, i.e. in Rayleigh–Bénard flow with Couette- or Poiseuille-type shear forcing, by extending the Grossmann & Lohse (J. Fluid Mech., vol. 407, 2000, pp. 27–56, Phys. Rev. Lett., vol. 86, 2001, pp. 3316–3319, Phys. Rev. E, vol. 66, 2002, 016305, Phys. Fluids, vol. 16, 2004, pp. 4462–4472) theory to sheared thermal convection. The control parameters for these systems are the Rayleigh number $Ra$, the Prandtl number $Pr$ and the Reynolds number $Re_S$ that characterises the strength of the imposed shear. By direct numerical simulations and theoretical considerations, we show that, in turbulent Rayleigh–Bénard convection, the friction coefficients associated with the applied shear and the shear generated by the large-scale convection rolls are both well described by Prandtl's (Ergeb. Aerodyn. Vers. Gött., vol. 4, 1932, pp. 18–29) logarithmic friction law, suggesting some kind of universality between purely shear-driven flows and thermal convection. These scaling relations hold well for $10^6 \leq Ra \leq 10^8$, $0.5 \leq Pr \leq 5.0$, and $0 \leq Re_S \leq 10^4$.

We derive the spin Euler equation for ideal flows by applying the spherical Clebsch mapping. This equation is based on the spin vector, a unit vector field encoding vortex lines, instead of the velocity. The spin Euler equation enables a feasible Lagrangian study of fluid dynamics, as the isosurface of a spin-vector component is a vortex surface and material surface in ideal flows. We establish a non-blowup criterion for the spin Euler equation, suggesting that the Laplacian of the spin vector must diverge if the solution forms a singularity at some finite time. The direct numerical simulations (DNS) of three ideal flows – the vortex knot, the vortex link and the modified Taylor–Green flow – are conducted by solving the spin Euler equation. The evolution of the Lagrangian vortex surface illustrates that the regions with large vorticity are rapidly stretched into spiral sheets. The DNS result exhibits a pronounced double-exponential growth of the maximum norm of Laplacian of the spin vector, showing no evidence of the finite-time singularity formation if the double-exponential growth holds at later times. Moreover, the present criterion with Lagrangian nature appears to be more sensitive than the Beale–Kato–Majda criterion in detecting the flows that are incapable of producing finite-time singularities.