Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T04:04:39.547Z Has data issue: false hasContentIssue false
  • English
  • Français

Worst-case amplification of disturbances in inertialess Couette flow of viscoelastic fluids

Published online by Cambridge University Press:  16 April 2013

Binh K. Lieu ,
Mihailo R. Jovanović  and
Satish Kumar
Binh K. Lieu
Affiliation:
Department of Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN 55455, USA
Mihailo R. Jovanović*
Affiliation:
Department of Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN 55455, USA
Satish Kumar
Affiliation:
Department of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Amplification of deterministic disturbances in inertialess shear-driven channel flows of viscoelastic fluids is examined by analysing the frequency responses from spatio-temporal body forces to the velocity and polymer stress fluctuations. In strongly elastic flows, we show that disturbances with large streamwise length scales may be significantly amplified even in the absence of inertia. For fluctuations without streamwise variations, we derive explicit analytical expressions for the dependence of the worst-case amplification (from different forcing to different velocity and polymer stress components) on the Weissenberg number (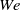$\mathit{We}$), the maximum extensibility of the polymer chains (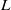$L$), the viscosity ratio and the spanwise wavenumber. For the Oldroyd-B model, the amplification of the most energetic components of velocity and polymer stress fields scales as 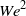${\mathit{We}}^{2} $ and 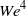${\mathit{We}}^{4} $. On the other hand, the finite extensibility of polymer molecules limits the largest achievable amplification even in flows with infinitely large Weissenberg numbers: in the presence of wall-normal and spanwise forces, the amplification of the streamwise velocity and polymer stress fluctuations is bounded by quadratic and quartic functions of 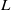$L$. This high amplification signals low robustness to modelling imperfections of inertialess channel flows of viscoelastic fluids. The underlying physical mechanism involves interactions of polymer stress fluctuations with a base shear, and it represents a close analogue of the lift-up mechanism that initiates a bypass transition in inertial flows of Newtonian fluids.

JFM classification

Non-Newtonian Flows: Non-Newtonian Flows Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 232 - 263
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arratia, P. E., Thomas, C. C., Diorio, J. & Gollub, J. P. 2006 Elastic instabilities of polymer solutions in cross-channel flow. Phys. Rev. Lett. 96, 144502.CrossRefGoogle ScholarPubMed
Bird, R. B., Curtiss, C. F., Armstrong, R. C. & Hassager, O. 1987 Dynamics of Polymeric Liquids, vol. 2. Wiley.Google Scholar
Bonn, D., Ingremeau, F., Amarouchene, Y. & Kellay, H. 2011 Large velocity fluctuations in small-Reynolds-number pipe flow of polymer solutions. Phys. Rev. E 84 (4), 045301.CrossRefGoogle ScholarPubMed
Boyd, S., Balakrishnan, V. & Kabamba, P. 1989 A bisection method for computing the ${h}_{\infty } $ norm of a transfer matrix and related problems. Math. Control Signal. 2 (3), 207–219.CrossRefGoogle Scholar
Bruinsma, N. A. & Steinbuch, M. 1990 A fast algorithm to compute the ${H}_{\infty } $ -norm of a transfer function matrix. Syst. Control Lett. 14, 287–293.CrossRefGoogle Scholar
Chilcott, M. D. & Rallison, J. M. 1988 Creeping flow of dilute polymer solutions past cylinders and spheres. J. Non-Newtonian Fluid Mech. 29, 381–432.CrossRefGoogle Scholar
Farrell, B. F. & Ioannou, P. J. 1993 Stochastic forcing of the linearized Navier–Stokes equations. Phys. Fluids A 5, 2600–2609.CrossRefGoogle Scholar
Groisman, A. & Steinberg, V. 2000 Elastic turbulence in a polymer solution flow. Nature 405, 53–55.CrossRefGoogle Scholar
Groisman, A. & Steinberg, V. 2001 Efficient mixing at low Reynolds numbers using polymer additives. Nature 410, 905–908.CrossRefGoogle ScholarPubMed
Groisman, A. & Steinberg, V. 2004 Elastic turbulence in curvilinear flows of polymer solutions. New J. Phys. 6, 29–48.CrossRefGoogle Scholar
Grossmann, S. 2000 The onset of shear flow turbulence. Rev. Mod. Phys. 72, 603–618.CrossRefGoogle Scholar
Hoda, N., Jovanović, M. R. & Kumar, S. 2008 Energy amplification in channel flows of viscoelastic fluids. J. Fluid Mech. 601, 407–424.CrossRefGoogle Scholar
Hoda, N., Jovanović, M. R. & Kumar, S. 2009 Frequency responses of streamwise-constant perturbations in channel flows of Oldroyd-B fluids. J. Fluid Mech. 625, 411–434.CrossRefGoogle Scholar
Jovanović, M. R. & Bamieh, B. 2005 Componentwise energy amplification in channel flows. J. Fluid Mech. 534, 145–183.CrossRefGoogle Scholar
Jovanović, M. R. & Kumar, S. 2010 Transient growth without inertia. Phys. Fluids 22 (2), 023101.CrossRefGoogle Scholar
Jovanović, M. R. & Kumar, S. 2011 Nonmodal amplification of stochastic disturbances in strongly elastic channel flows. J. Non-Newtonian Fluid Mech. 166 (14–15), 755–778.CrossRefGoogle Scholar
Larson, R. G. 1992 Instabilities in viscoelastic flows. Rheol. Acta 31, 213–263.CrossRefGoogle Scholar
Larson, R. G. 1999 The Structure and Rheology of Complex Fluids. Oxford University Press.Google Scholar
Larson, R. G. 2000 Turbulence without inertia. Nature 405, 27–28.CrossRefGoogle ScholarPubMed
Larson, R. G., Shaqfeh, E. S. G. & Muller, S. J. 1990 A purely elastic instability in Taylor–Couette flow. J. Fluid Mech. 218, 573–600.CrossRefGoogle Scholar
Lieu, B. K. & Jovanović, M. R. 2011 Computation of frequency responses of linear time-invariant PDEs on a compact interval. J. Comput. Phys. (submitted) arXiv: 1112.0579v1.Google Scholar
Meulenbroek, B., Storm, C., Morozov, A. N. & van Saarloos, W. 2004 Weakly nonlinear subcritical instability of visco-elastic Poiseuille flow. J. Non-Newtonian Fluid Mech. 116, 235–268.CrossRefGoogle Scholar
Morozov, A. N. & van Saarloos, W. 2005 Subcritical finite-amplitude solutions for plane Couette flow of viscoelastic fluids. Phys. Rev. Lett. 95, 024501.CrossRefGoogle ScholarPubMed
Ottino, J. M. & Wiggins, S. 2004 Introduction: mixing in microfluidics. Phil. Trans. R. Soc. Lond. A 362, 923–935.CrossRefGoogle ScholarPubMed
Pan, L., Morozov, A. & Arratia, P. 2011 Nonlinear elastic instabilities in parallel shear flows. In Bulletin of the American Physical Society, Vol. 56. Baltimore.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
Trefethen, L. N. & Embree, M. 2005 Spectra and Pseudospectra: the Behavior of Nonnormal Matrices and Operators. Princeton University Press.CrossRefGoogle Scholar
Trefethen, L. N., Hale, N., Platte, R. B., Driscoll, T. A. & Pachón, R. 2011 Chebfun version 4, University of Oxford. http://www.maths.ox.ac.uk/chebfun/.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoli, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261, 578–584.CrossRefGoogle ScholarPubMed
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.CrossRefGoogle Scholar
Weideman, J. A. C. & Reddy, S. C. 2000 A Matlab differentiation matrix suite. ACM Trans. Math. Softw. 26 (4), 465–519.CrossRefGoogle Scholar
Yesilata, B. 2002 Nonlinear dynamics of a highly viscous and elastic fluid in pipe flow. Fluid Dyn. Res. 31, 41–64.CrossRefGoogle Scholar
Yesilata, B. 2009 Temporal nature of polymeric flows near circular pipe-exit. Polym. Plast. Technol. Eng. 48 (7), 723–729.CrossRefGoogle Scholar
Zhou, K., Doyle, J. C. & Glover, K. 1996 Robust and Optimal Control. Prentice-Hall.Google Scholar