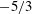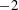1 Introduction
Wind energy is characterized by inherent variability. When wind farms are connected to an electricity grid, the power fluctuations need to be compensated by, e.g. ancillary power generators (Apt Reference Apt2007) or wind farm control (Shapiro et al. Reference Shapiro, Meyers, Meneveau and Gayme2016). It is thus important to understand over which time scales and with what magnitudes the power output fluctuates. This issue has motivated several studies on the spectral characteristics of the electrical power output from a wind farm or a cluster of wind farms (Apt Reference Apt2007; Katzenstein, Fertig & Apt Reference Katzenstein, Fertig and Apt2010; Vigueras-Rodríguez et al. Reference Vigueras-Rodríguez, Sørensen, Cutululis, Viedma and Donovan2010; Stevens & Meneveau Reference Stevens and Meneveau2014; Bandi Reference Bandi2017). Understanding the interaction between the wind turbines and the turbulent boundary layer, with its inherent statistical structure and presence of large coherent motions, is necessary for describing the resulting spectrum of the power output.
Apt (Reference Apt2007) analysed the spectrum of the power, aggregated over six turbines, and observed a power-law behaviour with a
![]() $f^{-5/3}$
scaling over four orders of magnitude in frequency. This observation raised the question of the relation between the spectrum and the scaling of the velocity fluctuations in the boundary layer, which follow a
$f^{-5/3}$
scaling over four orders of magnitude in frequency. This observation raised the question of the relation between the spectrum and the scaling of the velocity fluctuations in the boundary layer, which follow a
![]() $f^{-5/3}$
spectrum over a similar range of scales (Larsén, Larsen & Petersen Reference Larsén, Larsen and Petersen2016). Bandi (Reference Bandi2017) discussed how the spectrum of the power output from a single turbine scales similarly with that of the velocity fluctuations. In this analysis, Bandi (Reference Bandi2017) considered the structure function of the power output and showed how higher-order structure functions of velocity fluctuations scale similarly, considering inertial range scalings in analogy with Kolmogorov’s 1941 theory (Kolmogorov Reference Kolmogorov1941).
$f^{-5/3}$
spectrum over a similar range of scales (Larsén, Larsen & Petersen Reference Larsén, Larsen and Petersen2016). Bandi (Reference Bandi2017) discussed how the spectrum of the power output from a single turbine scales similarly with that of the velocity fluctuations. In this analysis, Bandi (Reference Bandi2017) considered the structure function of the power output and showed how higher-order structure functions of velocity fluctuations scale similarly, considering inertial range scalings in analogy with Kolmogorov’s 1941 theory (Kolmogorov Reference Kolmogorov1941).
For the sum of the power over many wind farms, the individual wind farm outputs can become uncorrelated on time scales related to local turbulence, because of the large geographical spacing. In this case, self correlation of the power signals becomes dominant, and is shown to lead to a limiting power-law scaling of
![]() $f^{-7/3}$
(Katzenstein et al.
Reference Katzenstein, Fertig and Apt2010; Bandi Reference Bandi2017). However, on the scale of a single wind farm, the wind turbine power outputs can show significant correlations (Stevens & Meneveau Reference Stevens and Meneveau2014; Bossuyt et al.
Reference Bossuyt, Howland, Meneveau and Meyers2017), which cannot be neglected in estimating the wind farm spectrum.
$f^{-7/3}$
(Katzenstein et al.
Reference Katzenstein, Fertig and Apt2010; Bandi Reference Bandi2017). However, on the scale of a single wind farm, the wind turbine power outputs can show significant correlations (Stevens & Meneveau Reference Stevens and Meneveau2014; Bossuyt et al.
Reference Bossuyt, Howland, Meneveau and Meyers2017), which cannot be neglected in estimating the wind farm spectrum.
For a fixed wind direction, large-eddy simulations by Stevens & Meneveau (Reference Stevens and Meneveau2014), and later wind tunnel experiments by Bossuyt et al. (Reference Bossuyt, Howland, Meneveau and Meyers2016), confirmed power-law behaviour with a slope close to
![]() $-5/3$
for the spectrum of the aggregate wind farm power output. The measured spectra also showed a peak at a frequency corresponding to the convective travel time between streamwise aligned turbines. Moreover, it was observed that the power-law region extends to frequencies that are significantly lower than observed in the spectrum of any individual wind turbine. By artificially decorrelating the measured wind turbine power signals in time, Bossuyt et al. (Reference Bossuyt, Howland, Meneveau and Meyers2016) confirmed the importance of the spatio-temporal correlation between wind turbine power outputs in generating these specific spectral characteristics.
$-5/3$
for the spectrum of the aggregate wind farm power output. The measured spectra also showed a peak at a frequency corresponding to the convective travel time between streamwise aligned turbines. Moreover, it was observed that the power-law region extends to frequencies that are significantly lower than observed in the spectrum of any individual wind turbine. By artificially decorrelating the measured wind turbine power signals in time, Bossuyt et al. (Reference Bossuyt, Howland, Meneveau and Meyers2016) confirmed the importance of the spatio-temporal correlation between wind turbine power outputs in generating these specific spectral characteristics.
In this paper we consider the fundamental question whether power fluctuations in wind farms can be related to the structure of turbulence in boundary layers. Specifically, we interpret the interaction between the array of wind turbines and the turbulent boundary layer as a discrete spatial sampling in order to model and explain how the wind farm frequency spectrum is composed. The analysis is done by making use of a model parametrization for the wavenumber–frequency spectrum of the streamwise velocity in high Reynolds number turbulent boundary layers (Wilczek, Stevens & Meneveau Reference Wilczek, Stevens and Meneveau2015a ). In § 2 an overview of the results from the wind tunnel experiment are given including main characteristics of the experimental set-up. Based on these observations, a model for the wind farm frequency spectrum is developed in § 3. The model is compared with experimental data and conclusions are provided in § 4.
2 Experimental data

Figure 1. (a) Photograph of the micro wind farm and (b) measurement results for the surrogate power output spectra from the wind tunnel study by Bossuyt et al. (Reference Bossuyt, Howland, Meneveau and Meyers2016).
A wind tunnel study was performed based on a model (‘micro’) wind farm consisting of 100 porous disk models with a thrust coefficient
![]() $C_{T}=0.75\pm 0.04$
(Bossuyt et al.
Reference Bossuyt, Howland, Meneveau and Meyers2017). The porous disk models have a diameter of
$C_{T}=0.75\pm 0.04$
(Bossuyt et al.
Reference Bossuyt, Howland, Meneveau and Meyers2017). The porous disk models have a diameter of
![]() $D=3~\text{cm}$
and a hub height of
$D=3~\text{cm}$
and a hub height of
![]() $2.3~\text{cm}$
. Each model is instrumented with two strain gauges and calibrated to measure the instantaneous thrust force. By using standard relations from momentum theory, one may deduce the incoming spatially averaged velocity
$2.3~\text{cm}$
. Each model is instrumented with two strain gauges and calibrated to measure the instantaneous thrust force. By using standard relations from momentum theory, one may deduce the incoming spatially averaged velocity
![]() $\langle u\rangle _{i}$
for porous disk
$\langle u\rangle _{i}$
for porous disk
![]() $i$
from the time signal of the thrust force with
$i$
from the time signal of the thrust force with
![]() $F_{i}(t)\approx (1/2)\unicode[STIX]{x1D70C}C_{T}A\langle u\rangle _{i}^{2}(t)$
. The instantaneous equivalent power output,
$F_{i}(t)\approx (1/2)\unicode[STIX]{x1D70C}C_{T}A\langle u\rangle _{i}^{2}(t)$
. The instantaneous equivalent power output,
![]() $P_{i}(t)$
, is then deduced by assuming a typical wind turbine power coefficient
$P_{i}(t)$
, is then deduced by assuming a typical wind turbine power coefficient
![]() $C_{P}$
, such that
$C_{P}$
, such that
![]() $P_{i}(t)\approx (1/2)\unicode[STIX]{x1D70C}C_{P}A\langle u\rangle _{i}^{3}(t)$
. Here,
$P_{i}(t)\approx (1/2)\unicode[STIX]{x1D70C}C_{P}A\langle u\rangle _{i}^{3}(t)$
. Here,
![]() $A=\unicode[STIX]{x03C0}D^{2}/4$
is the rotor area and
$A=\unicode[STIX]{x03C0}D^{2}/4$
is the rotor area and
![]() $\unicode[STIX]{x1D70C}$
the air density. This signal is a surrogate power signal for a wind turbine. Considering the effect of the spatial filtering by the disk, the frequency response of the models goes up to
$\unicode[STIX]{x1D70C}$
the air density. This signal is a surrogate power signal for a wind turbine. Considering the effect of the spatial filtering by the disk, the frequency response of the models goes up to
![]() $fD/U\approx 0.6$
, where
$fD/U\approx 0.6$
, where
![]() $f$
is the frequency and
$f$
is the frequency and
![]() $U$
the mean velocity at hub height. This is sufficiently high for the time scales considered here. The wind farm layout consists of an array with
$U$
the mean velocity at hub height. This is sufficiently high for the time scales considered here. The wind farm layout consists of an array with
![]() $5$
streamwise aligned columns and
$5$
streamwise aligned columns and
![]() $20$
rows, with a streamwise and spanwise spacing of
$20$
rows, with a streamwise and spanwise spacing of
![]() $S_{x}=7D$
and
$S_{x}=7D$
and
![]() $S_{y}=5D$
. Instantaneous measurements of the thrust force were performed for the sixty models in the three central columns of the micro wind farm. Figure 1(a) shows a photograph of an aligned layout. A staggered layout is created by sliding the even rows in the spanwise direction.
$S_{y}=5D$
. Instantaneous measurements of the thrust force were performed for the sixty models in the three central columns of the micro wind farm. Figure 1(a) shows a photograph of an aligned layout. A staggered layout is created by sliding the even rows in the spanwise direction.
The incoming velocity profile is measured with a hot-wire probe
![]() $0.21~\text{m}$
upstream of the wind farm. The measured boundary layer height is
$0.21~\text{m}$
upstream of the wind farm. The measured boundary layer height is
![]() $\unicode[STIX]{x1D6FF}_{99}=0.16~\text{m}$
, with the models operating in the log region of the boundary layer and with an incoming velocity at hub height of
$\unicode[STIX]{x1D6FF}_{99}=0.16~\text{m}$
, with the models operating in the log region of the boundary layer and with an incoming velocity at hub height of
![]() $U=11.8~\text{m}~\text{s}^{-1}$
. The measured roughness length is
$U=11.8~\text{m}~\text{s}^{-1}$
. The measured roughness length is
![]() $z_{0}=0.9\times 10^{-2}~\text{mm}$
, the friction velocity is
$z_{0}=0.9\times 10^{-2}~\text{mm}$
, the friction velocity is
![]() $u_{\unicode[STIX]{x1D70F}}=0.6~\text{m}~\text{s}^{-1}$
and the root-mean-square of the velocity is
$u_{\unicode[STIX]{x1D70F}}=0.6~\text{m}~\text{s}^{-1}$
and the root-mean-square of the velocity is
![]() $u_{rms}=1.28~\text{m}~\text{s}^{-1}$
. With a geometric scaling factor of
$u_{rms}=1.28~\text{m}~\text{s}^{-1}$
. With a geometric scaling factor of
![]() $1:3333$
, the measurement set-up represents a full-scale wind farm operating in a neutral and moderately rough boundary layer. The measurement time for each case is 5 minutes or more. This is over
$1:3333$
, the measurement set-up represents a full-scale wind farm operating in a neutral and moderately rough boundary layer. The measurement time for each case is 5 minutes or more. This is over
![]() $3\times 10^{4}$
times the largest integral time scale measured in the boundary layer, so that well-converged statistics are obtained. More information can be found in Bossuyt et al. (Reference Bossuyt, Howland, Meneveau and Meyers2017).
$3\times 10^{4}$
times the largest integral time scale measured in the boundary layer, so that well-converged statistics are obtained. More information can be found in Bossuyt et al. (Reference Bossuyt, Howland, Meneveau and Meyers2017).
Figure 1(b) shows the power spectral density of relative power fluctuations
![]() $P^{\prime }(t)/\overline{P}$
(we denote the temporal mean with an overbar and the temporal fluctuation with a prime), which are reconstructed from the strain gauge measurements (Bossuyt et al.
Reference Bossuyt, Howland, Meneveau and Meyers2017). Throughout this paper we normalize the variables where possible by scales of interest to wind farms, such as the streamwise spacing
$P^{\prime }(t)/\overline{P}$
(we denote the temporal mean with an overbar and the temporal fluctuation with a prime), which are reconstructed from the strain gauge measurements (Bossuyt et al.
Reference Bossuyt, Howland, Meneveau and Meyers2017). Throughout this paper we normalize the variables where possible by scales of interest to wind farms, such as the streamwise spacing
![]() $S_{x}$
, the hub-height velocity
$S_{x}$
, the hub-height velocity
![]() $U$
and the friction velocity
$U$
and the friction velocity
![]() $u_{\unicode[STIX]{x1D70F}}$
. When variables are not normalized, we display the corresponding units. For an aligned layout, the spectrum for an individual model in each row is plotted in blue to yellow colours. Also shown are the spectra for the aggregated wind farm power of an aligned (black) and staggered (red) wind farm. For comparison, the dashed lines show the spectra when the individual power signals from each model are first decorrelated in time (by shifting the entire time series by arbitrary, large, time delays) before aggregating and calculating the spectral density. The spectra for individual models show the increase in variability with increasing row number, due to the added wake turbulence.
$u_{\unicode[STIX]{x1D70F}}$
. When variables are not normalized, we display the corresponding units. For an aligned layout, the spectrum for an individual model in each row is plotted in blue to yellow colours. Also shown are the spectra for the aggregated wind farm power of an aligned (black) and staggered (red) wind farm. For comparison, the dashed lines show the spectra when the individual power signals from each model are first decorrelated in time (by shifting the entire time series by arbitrary, large, time delays) before aggregating and calculating the spectral density. The spectra for individual models show the increase in variability with increasing row number, due to the added wake turbulence.
The aggregated wind farm spectra show the features mentioned above: a peak at
![]() $fS_{x}/U=1$
when the layout is aligned and
$fS_{x}/U=1$
when the layout is aligned and
![]() $fS_{x}/U\approx 0.5$
when staggered, a second smaller peak at twice this frequency and a power-law region with a slope slightly steeper than
$fS_{x}/U\approx 0.5$
when staggered, a second smaller peak at twice this frequency and a power-law region with a slope slightly steeper than
![]() $-5/3$
up to lower frequencies than observed for any individual model. When the power signals are artificially decorrelated in time, these features are not observed in the resulting spectrum. This difference illustrates the crucial role of the spatio-temporal correlation in the boundary layer and the specific frequency ranges over which the individual power signals show a correlation (e.g.
$-5/3$
up to lower frequencies than observed for any individual model. When the power signals are artificially decorrelated in time, these features are not observed in the resulting spectrum. This difference illustrates the crucial role of the spatio-temporal correlation in the boundary layer and the specific frequency ranges over which the individual power signals show a correlation (e.g.
![]() $0.1<fS_{x}/U$
and
$0.1<fS_{x}/U$
and
![]() $fS_{x}/U\approx 1,2,\ldots$
for the aligned layout) or anti-correlation (e.g.
$fS_{x}/U\approx 1,2,\ldots$
for the aligned layout) or anti-correlation (e.g.
![]() $0.1<fS_{x}/U<0.9$
for the staggered layout). For the staggered layout the peaks shift to lower frequencies as the streamwise spacing between aligned turbines has doubled. It is also observed that the power-law range extends to lower frequencies when the layout is staggered. In the next section we aim at providing a quantitative description of these measurements based on an analytically tractable model for the spatio-temporal structure of high Reynolds number boundary layer turbulence.
$0.1<fS_{x}/U<0.9$
for the staggered layout). For the staggered layout the peaks shift to lower frequencies as the streamwise spacing between aligned turbines has doubled. It is also observed that the power-law range extends to lower frequencies when the layout is staggered. In the next section we aim at providing a quantitative description of these measurements based on an analytically tractable model for the spatio-temporal structure of high Reynolds number boundary layer turbulence.
3 Modelling of the wind farm power output frequency spectrum
In the first part of this section, the relation between the wind turbine power and velocity fluctuations is discussed. This will allow the use of a recently developed parametrization for the wavenumber–frequency spectrum of the velocity (Wilczek et al. Reference Wilczek, Stevens and Meneveau2015a ), as discussed in the second part. Then, a transfer function to represent the discrete spatial sampling of the boundary layer is derived. Both are then combined to find the frequency spectrum of the wind farm power output. This section is concluded with a validation of the model with experimental data.
3.1 Power fluctuations
The power output of a wind turbine
![]() $P_{i}(t)$
is generated by the forces acting on the blades as they sweep through the flow field. At a typical tip speed ratio of the order of 5–10, the blade tips sweep through the flow
$P_{i}(t)$
is generated by the forces acting on the blades as they sweep through the flow field. At a typical tip speed ratio of the order of 5–10, the blade tips sweep through the flow
![]() $5-10$
times faster than the incoming velocity. The focus of this study is on turbulent length scales that are significantly larger than the turbine diameter, i.e. comparable to the streamwise turbine spacing or larger. Over the corresponding time scales, the blades make multiple full rotations within the time for turbulent eddies of these scales to pass through the wind turbine. The turbine power can therefore be expressed in terms of the disk average power of the air flowing through the rotor area (we denote the spatial average with angle brackets)
$5-10$
times faster than the incoming velocity. The focus of this study is on turbulent length scales that are significantly larger than the turbine diameter, i.e. comparable to the streamwise turbine spacing or larger. Over the corresponding time scales, the blades make multiple full rotations within the time for turbulent eddies of these scales to pass through the wind turbine. The turbine power can therefore be expressed in terms of the disk average power of the air flowing through the rotor area (we denote the spatial average with angle brackets)
![]() $P_{air}(t)=(1/2)\unicode[STIX]{x1D70C}A\langle u\rangle ^{3}(t)$
and the instantaneous power coefficient of the wind turbine
$P_{air}(t)=(1/2)\unicode[STIX]{x1D70C}A\langle u\rangle ^{3}(t)$
and the instantaneous power coefficient of the wind turbine
![]() $C_{P}(t)$
(Milan, Wächter & Peinke Reference Milan, Wächter and Peinke2013), thereby neglecting higher-order terms and leading to
$C_{P}(t)$
(Milan, Wächter & Peinke Reference Milan, Wächter and Peinke2013), thereby neglecting higher-order terms and leading to
![]() $P_{i}(t)\approx (1/2)\unicode[STIX]{x1D70C}AC_{P}(t){\langle u\rangle _{i}}^{3}(t)$
for wind turbine
$P_{i}(t)\approx (1/2)\unicode[STIX]{x1D70C}AC_{P}(t){\langle u\rangle _{i}}^{3}(t)$
for wind turbine
![]() $i$
.
$i$
.
Focusing on the below-rated operating regime, wind turbines are controlled to maximize aerodynamic efficiency. In this regime, the overall turbine power coefficient
![]() $C_{P}(t)$
is kept maximal and can be considered nearly constant (Aho et al.
Reference Aho, Buckspan, Laks, Fleming, Jeong, Dunne, Churchfield, Pao and Johnson2012). Furthermore, power fluctuations are significantly less sensitive to changes in
$C_{P}(t)$
is kept maximal and can be considered nearly constant (Aho et al.
Reference Aho, Buckspan, Laks, Fleming, Jeong, Dunne, Churchfield, Pao and Johnson2012). Furthermore, power fluctuations are significantly less sensitive to changes in
![]() $C_{P}(t)$
then to velocity fluctuations (Theunissen et al.
Reference Theunissen, Housley, Allen and Carey2015). With a constant power coefficient, the instantaneous turbine power depends on the cube of the velocity, as given by
$C_{P}(t)$
then to velocity fluctuations (Theunissen et al.
Reference Theunissen, Housley, Allen and Carey2015). With a constant power coefficient, the instantaneous turbine power depends on the cube of the velocity, as given by
![]() $P_{i}(t)\approx C_{1}{\langle u\rangle _{i}}^{3}(t)$
and with
$P_{i}(t)\approx C_{1}{\langle u\rangle _{i}}^{3}(t)$
and with
![]() $C_{1}=\unicode[STIX]{x1D70C}AC_{P}/2$
a constant.
$C_{1}=\unicode[STIX]{x1D70C}AC_{P}/2$
a constant.
The spatially averaged velocity is decomposed in a temporal mean and fluctuating part:
![]() $\langle u\rangle =\overline{\langle u\rangle }+\langle u\rangle ^{\prime }$
, to express the power fluctuations in terms of the velocity fluctuations:
$\langle u\rangle =\overline{\langle u\rangle }+\langle u\rangle ^{\prime }$
, to express the power fluctuations in terms of the velocity fluctuations:
with
![]() $C_{2}=(3/2)\unicode[STIX]{x1D70C}AC_{P}\overline{\langle u\rangle }^{2}$
. Equation (3.3) involves neglecting higher-order terms. For typical atmospheric conditions over reasonably short time intervals over which nearly stationary conditions can be assumed (e.g. 10–20 min), it is acceptable to assume
$C_{2}=(3/2)\unicode[STIX]{x1D70C}AC_{P}\overline{\langle u\rangle }^{2}$
. Equation (3.3) involves neglecting higher-order terms. For typical atmospheric conditions over reasonably short time intervals over which nearly stationary conditions can be assumed (e.g. 10–20 min), it is acceptable to assume
![]() $\langle u\rangle ^{\prime }/\overline{\langle u\rangle }\ll 1$
(e.g. measurements at the Horns Rev wind farm show
$\langle u\rangle ^{\prime }/\overline{\langle u\rangle }\ll 1$
(e.g. measurements at the Horns Rev wind farm show
![]() $TI_{u}=(\overline{{u^{\prime }}^{2}})^{1/2}/\overline{u}\approx 0.05{-}0.1$
(Hansen et al.
Reference Hansen, Barthelmie, Jensen and Sommer2012)), so that the higher-order terms can be neglected as a first approximation.
$TI_{u}=(\overline{{u^{\prime }}^{2}})^{1/2}/\overline{u}\approx 0.05{-}0.1$
(Hansen et al.
Reference Hansen, Barthelmie, Jensen and Sommer2012)), so that the higher-order terms can be neglected as a first approximation.
With these simplifications, the power fluctuations are shown to scale approximately linearly with the disk-averaged velocity fluctuations. As shown by Bandi (Reference Bandi2017), higher powers of
![]() $u^{\prime }$
scale similarly, providing further justification for the simplifications used. The spectrum of the aggregated wind farm power
$u^{\prime }$
scale similarly, providing further justification for the simplifications used. The spectrum of the aggregated wind farm power
![]() $(P_{WF}=\sum P_{i})$
can thus be considered as a discrete spatial sampling of the fluctuating disk-averaged velocity field.
$(P_{WF}=\sum P_{i})$
can thus be considered as a discrete spatial sampling of the fluctuating disk-averaged velocity field.
3.2 Spatio-temporal flow description
To evaluate the frequency spectrum of the power output of an array of turbines with a given spatial distribution, a description for the space–time correlation of the boundary layer is required. To this end, we use the model developed by Wilczek et al. (Reference Wilczek, Stevens and Meneveau2015a ) for the spectral analogue, the wavenumber–frequency spectral density, as given by:
Here,
![]() $U$
is the convective velocity, taken to be a mean velocity at hub height in the
$U$
is the convective velocity, taken to be a mean velocity at hub height in the
![]() $x$
direction,
$x$
direction,
![]() $\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}f$
the angular velocity,
$\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}f$
the angular velocity,
![]() $E_{kk}(k_{1},k_{2})$
the wavenumber spectrum of the streamwise velocity fluctuations (see appendix A for definitions of the spectra) and
$E_{kk}(k_{1},k_{2})$
the wavenumber spectrum of the streamwise velocity fluctuations (see appendix A for definitions of the spectra) and
![]() $\boldsymbol{v}$
a random sweeping velocity in the horizontal direction.
$\boldsymbol{v}$
a random sweeping velocity in the horizontal direction.
The approach is developed in a horizontal plane at hub height
![]() $z$
and spanning the streamwise
$z$
and spanning the streamwise
![]() $k_{1}$
and spanwise
$k_{1}$
and spanwise
![]() $k_{2}$
directions, where we assume horizontal homogeneous flow properties. The spatial averaging of the velocity over the rotor area in the vertical direction is not considered, but takes place at smaller length and corresponding time scales (of the order of the diameter) than those of interest (of the order of the streamwise spacing and larger). Thereby, the height dependence of the spatio-temporal flow structure (Wilczek, Stevens & Meneveau Reference Wilczek, Stevens and Meneveau2015b
) over the rotor height is not considered, and is expected to slightly smear out the spectrum over the frequency axis.
$k_{2}$
directions, where we assume horizontal homogeneous flow properties. The spatial averaging of the velocity over the rotor area in the vertical direction is not considered, but takes place at smaller length and corresponding time scales (of the order of the diameter) than those of interest (of the order of the streamwise spacing and larger). Thereby, the height dependence of the spatio-temporal flow structure (Wilczek, Stevens & Meneveau Reference Wilczek, Stevens and Meneveau2015b
) over the rotor height is not considered, and is expected to slightly smear out the spectrum over the frequency axis.
We use the analytical form for the spatial two-dimensional (2-D) spectrum
![]() $E_{kk}(k_{1},k_{2})$
and the necessary parameters as provided by Wilczek et al. (Reference Wilczek, Stevens and Meneveau2015a
). This analytical spectrum assumes a classical scaling for the logarithmic and inertial range regions of streamwise wavenumbers in turbulent boundary layers (e.g.
$E_{kk}(k_{1},k_{2})$
and the necessary parameters as provided by Wilczek et al. (Reference Wilczek, Stevens and Meneveau2015a
). This analytical spectrum assumes a classical scaling for the logarithmic and inertial range regions of streamwise wavenumbers in turbulent boundary layers (e.g.
![]() $k_{1}^{-1}$
and
$k_{1}^{-1}$
and
![]() $k_{1}^{-5/3}$
), see Nickels et al. (Reference Nickels, Marusic, Hafez and Chong2005). The high wavenumber range of this spectrum,
$k_{1}^{-5/3}$
), see Nickels et al. (Reference Nickels, Marusic, Hafez and Chong2005). The high wavenumber range of this spectrum,
![]() $E_{kk}^{{>}}(k_{1},k_{2})$
, is modelled by an infinitely extended inertial range:
$E_{kk}^{{>}}(k_{1},k_{2})$
, is modelled by an infinitely extended inertial range:
with
![]() $k=\sqrt{k_{1}^{2}+k_{2}^{2}}$
,
$k=\sqrt{k_{1}^{2}+k_{2}^{2}}$
,
![]() $C_{K}\approx 1.6$
the Kolmogorov constant,
$C_{K}\approx 1.6$
the Kolmogorov constant,
![]() $\unicode[STIX]{x1D716}=u_{\unicode[STIX]{x1D70F}}^{3}/(\unicode[STIX]{x1D705}z)$
an estimate for the energy dissipation and
$\unicode[STIX]{x1D716}=u_{\unicode[STIX]{x1D70F}}^{3}/(\unicode[STIX]{x1D705}z)$
an estimate for the energy dissipation and
![]() $\unicode[STIX]{x1D705}\approx 0.4$
the von Kármán constant, such that
$\unicode[STIX]{x1D705}\approx 0.4$
the von Kármán constant, such that
![]() $(\unicode[STIX]{x1D6E4}(1/3)C_{K})/(5\sqrt{\unicode[STIX]{x03C0}}\unicode[STIX]{x1D6E4}(5/6))\approx 0.268$
. For the low wavenumbers, a
$(\unicode[STIX]{x1D6E4}(1/3)C_{K})/(5\sqrt{\unicode[STIX]{x03C0}}\unicode[STIX]{x1D6E4}(5/6))\approx 0.268$
. For the low wavenumbers, a
![]() $k_{1}^{-1}$
region is transitioned to a constant spectrum by:
$k_{1}^{-1}$
region is transitioned to a constant spectrum by:
with the exponent
![]() $\unicode[STIX]{x1D6FD}=4$
and
$\unicode[STIX]{x1D6FD}=4$
and
![]() $H$
a length scale for the boundary layer height. These two ranges are blended together to form the complete wavenumber spectrum:
$H$
a length scale for the boundary layer height. These two ranges are blended together to form the complete wavenumber spectrum:
with
![]() $\unicode[STIX]{x1D703}(kz)=(\tanh (\unicode[STIX]{x1D6FC}\log (kz))+1)/2$
and
$\unicode[STIX]{x1D703}(kz)=(\tanh (\unicode[STIX]{x1D6FC}\log (kz))+1)/2$
and
![]() $\unicode[STIX]{x1D6FC}=4$
. The height dependent amplitude
$\unicode[STIX]{x1D6FC}=4$
. The height dependent amplitude
![]() $D(z)$
for the low wavenumber range is determined numerically such that
$D(z)$
for the low wavenumber range is determined numerically such that
![]() $\int E_{kk}\,\text{d}k_{1}\,\text{d}k_{2}=u_{rms}^{2}$
. The wavenumber spectrum is thereby defined by three parameters:
$\int E_{kk}\,\text{d}k_{1}\,\text{d}k_{2}=u_{rms}^{2}$
. The wavenumber spectrum is thereby defined by three parameters:
![]() $H$
,
$H$
,
![]() $u_{\unicode[STIX]{x1D70F}}$
and
$u_{\unicode[STIX]{x1D70F}}$
and
![]() $u_{rms}$
. In projecting
$u_{rms}$
. In projecting
![]() $E_{kk}$
to the wavenumber–frequency domain with (3.4), the term
$E_{kk}$
to the wavenumber–frequency domain with (3.4), the term
![]() $\langle (\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{k})^{2}\rangle$
is modelled as
$\langle (\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{k})^{2}\rangle$
is modelled as
![]() $\langle (\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{k})^{2}\rangle =u_{rms}^{2}(k_{1}^{2}+Ck_{2}^{2})$
, with
$\langle (\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{k})^{2}\rangle =u_{rms}^{2}(k_{1}^{2}+Ck_{2}^{2})$
, with
![]() $C\approx 0.41$
(Wilczek et al.
Reference Wilczek, Stevens and Meneveau2015a
).
$C\approx 0.41$
(Wilczek et al.
Reference Wilczek, Stevens and Meneveau2015a
).

Figure 2. (a) Comparison of the modelled frequency spectrum
![]() $E_{\unicode[STIX]{x1D714}}$
with the measured hot-wire spectrum upstream of the scaled wind farm and (b) the corresponding modelled streamwise wavenumber–frequency spectrum
$E_{\unicode[STIX]{x1D714}}$
with the measured hot-wire spectrum upstream of the scaled wind farm and (b) the corresponding modelled streamwise wavenumber–frequency spectrum
![]() $4\unicode[STIX]{x03C0}^{2}UE_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})/(u_{\unicode[STIX]{x1D70F}}^{2}S_{x}^{2})$
. The horizontal green and red lines indicate the location of two cuts of the spectrum, discussed in § 3.4 and shown in figure 4.
$4\unicode[STIX]{x03C0}^{2}UE_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})/(u_{\unicode[STIX]{x1D70F}}^{2}S_{x}^{2})$
. The horizontal green and red lines indicate the location of two cuts of the spectrum, discussed in § 3.4 and shown in figure 4.
In figure 2(a) we compare the spectrum measured by the hot-wire probe in the wind tunnel experiment upstream from the wind farm, with the 1-D spectrum implied by this model (
![]() $E_{\unicode[STIX]{x1D714}}=\iint \unicode[STIX]{x1D6F7}_{11}(k_{1},k_{2},\unicode[STIX]{x1D714})\,\text{d}k_{1}\,\text{d}k_{2}$
) and based on the values for
$E_{\unicode[STIX]{x1D714}}=\iint \unicode[STIX]{x1D6F7}_{11}(k_{1},k_{2},\unicode[STIX]{x1D714})\,\text{d}k_{1}\,\text{d}k_{2}$
) and based on the values for
![]() $H=\unicode[STIX]{x1D6FF}_{99}$
,
$H=\unicode[STIX]{x1D6FF}_{99}$
,
![]() $u_{\unicode[STIX]{x1D70F}}$
and
$u_{\unicode[STIX]{x1D70F}}$
and
![]() $u_{rms}$
from the hot-wire measurement (see § 2). The hot-wire spectrum is estimated by averaging over windowed segments. Because the time length of the hot-wire signal is limited, the spectrum is estimated once by averaging over
$u_{rms}$
from the hot-wire measurement (see § 2). The hot-wire spectrum is estimated by averaging over windowed segments. Because the time length of the hot-wire signal is limited, the spectrum is estimated once by averaging over
![]() $10$
segments to cover the lowest frequencies, and once over
$10$
segments to cover the lowest frequencies, and once over
![]() $50$
shorter windows for a better estimate of the higher frequency range. A Hanning window is used and the
$50$
shorter windows for a better estimate of the higher frequency range. A Hanning window is used and the
![]() $95\,\%$
confidence bounds are shown, as estimated by the pwelch routine in Matlab™. Overall, the agreement is acceptable and mostly within the uncertainty bounds for high frequencies. Note that the dissipation range is not modelled as it takes place at scales significantly smaller than those of interest. The modelled spectrum has a slightly lower energy at the lowest frequencies. This is caused by the higher modelled spectrum where the
$95\,\%$
confidence bounds are shown, as estimated by the pwelch routine in Matlab™. Overall, the agreement is acceptable and mostly within the uncertainty bounds for high frequencies. Note that the dissipation range is not modelled as it takes place at scales significantly smaller than those of interest. The modelled spectrum has a slightly lower energy at the lowest frequencies. This is caused by the higher modelled spectrum where the
![]() $-1$
and
$-1$
and
![]() $-5/3$
regions are blended, which results in a smaller parameter
$-5/3$
regions are blended, which results in a smaller parameter
![]() $D(z)$
and a lower spectrum or correlation in the low frequency and wavenumber ranges. This limitation of the modelled spectrum should be kept in mind when modelled wind farm spectra are compared with experimental data, as further discussed in § 3.5. The streamwise wavenumber–frequency spectrum
$D(z)$
and a lower spectrum or correlation in the low frequency and wavenumber ranges. This limitation of the modelled spectrum should be kept in mind when modelled wind farm spectra are compared with experimental data, as further discussed in § 3.5. The streamwise wavenumber–frequency spectrum
![]() $E_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})=\int \unicode[STIX]{x1D6F7}_{11}(k_{1},k_{2},\unicode[STIX]{x1D714})\,\text{d}k_{2}$
from the model using the measured hot-wire parameters, is shown in figure 2(b).
$E_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})=\int \unicode[STIX]{x1D6F7}_{11}(k_{1},k_{2},\unicode[STIX]{x1D714})\,\text{d}k_{2}$
from the model using the measured hot-wire parameters, is shown in figure 2(b).
Inside the wind farm, the wind turbines interact with the boundary layer by producing wakes with a lower velocity and added turbulence, thereby modulating the spatio-temporal structure in some degree. These effects result in a deviation from the classical scaling for the velocity spectra in a turbulent boundary layer. However, it is experimentally extremely challenging to measure the full wavenumber–frequency spectrum of such a large domain. Furthermore, from the cross-correlation results in Bossuyt et al. (Reference Bossuyt, Howland, Meneveau and Meyers2017) it is clear that inside the wind farm the large scale spatio-temporal structure of the flow is still very similar to that of a classical turbulent boundary layer, but with an increased decorrelation due to the turbine wakes. We thus use the wavenumber–frequency spectrum for the boundary layer in front of the wind farm to characterize the baseline flow properties that are sampled by the array of turbines.
3.3 Spatial sampling transfer function
The fluctuating part of the wind farm power is evaluated as the sum of the fluctuations of each turbine, according to:
![]() $P_{WF}^{\prime }=\sum P_{i}^{\prime }\approx C_{2}\sum \langle u\rangle _{i}^{\prime }$
(see (3.3)), where we assume that
$P_{WF}^{\prime }=\sum P_{i}^{\prime }\approx C_{2}\sum \langle u\rangle _{i}^{\prime }$
(see (3.3)), where we assume that
![]() $C_{2}$
is the same for all turbines. Consequently, the sampling of the velocity field by the wind farm can be expressed as a convolution evaluated at the wind farm position, e.g.
$C_{2}$
is the same for all turbines. Consequently, the sampling of the velocity field by the wind farm can be expressed as a convolution evaluated at the wind farm position, e.g.
![]() $P_{WF}^{\prime }(t)\approx C_{2}\iint g(x,y)u^{\prime }(x,y,t)\,\text{d}x\,\text{d}y$
, where
$P_{WF}^{\prime }(t)\approx C_{2}\iint g(x,y)u^{\prime }(x,y,t)\,\text{d}x\,\text{d}y$
, where
![]() $g(x,y)$
is the wind farm sampling kernel. This function represents the sum over all turbines as well as the spatial averaging over the rotor area of each wind turbine. The latter is here modelled with a Dirac impulse at the location of turbine
$g(x,y)$
is the wind farm sampling kernel. This function represents the sum over all turbines as well as the spatial averaging over the rotor area of each wind turbine. The latter is here modelled with a Dirac impulse at the location of turbine
![]() $i$
and a box filter with width equal to the turbine diameter. The wind farm sampling function is given by:
$i$
and a box filter with width equal to the turbine diameter. The wind farm sampling function is given by:
Analogous to the power spectrum of the wind farm power output, we consider the spatial filtering of the energy spectrum of the streamwise velocity
![]() $\unicode[STIX]{x1D6F7}_{11}(k_{1},k_{2},\unicode[STIX]{x1D714})$
, by the respective transfer function
$\unicode[STIX]{x1D6F7}_{11}(k_{1},k_{2},\unicode[STIX]{x1D714})$
, by the respective transfer function
![]() $\widehat{g}(k_{1},k_{2})$
(Maidanik & Jorgensen Reference Maidanik and Jorgensen1967):
$\widehat{g}(k_{1},k_{2})$
(Maidanik & Jorgensen Reference Maidanik and Jorgensen1967):
where the tilde indicates the spatial sampling. The frequency spectrum can then be found by integrating over all wavenumbers:
so that the filtered energy spectrum is connected to the spectrum of the wind farm power output by
![]() $PSD(P_{WF}^{\prime })\approx C_{2}^{2}\widetilde{E}_{\unicode[STIX]{x1D714}}$
. The transfer function
$PSD(P_{WF}^{\prime })\approx C_{2}^{2}\widetilde{E}_{\unicode[STIX]{x1D714}}$
. The transfer function
![]() $\widehat{g}(k_{1},k_{2})$
is found by taking
$\widehat{g}(k_{1},k_{2})$
is found by taking
![]() $2\unicode[STIX]{x03C0}$
times the Fourier transform of the physical-space filter function in each direction (see appendix B for details):
$2\unicode[STIX]{x03C0}$
times the Fourier transform of the physical-space filter function in each direction (see appendix B for details):
 $$\begin{eqnarray}\displaystyle {\hat{g}}(k_{1},k_{2}) & = & \displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }g(x,y)\exp (-\text{i}k_{1}x)\exp (-\text{i}k_{2}y)\,\text{d}x\,\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\mathop{\sum }_{i=1}^{N}\exp (-\text{i}(k_{1}x_{i}+k_{2}y_{i})),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\hat{g}}(k_{1},k_{2}) & = & \displaystyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }g(x,y)\exp (-\text{i}k_{1}x)\exp (-\text{i}k_{2}y)\,\text{d}x\,\text{d}y\nonumber\\ \displaystyle & = & \displaystyle \frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\mathop{\sum }_{i=1}^{N}\exp (-\text{i}(k_{1}x_{i}+k_{2}y_{i})),\end{eqnarray}$$
resulting in:
 $$\begin{eqnarray}\displaystyle |\widehat{g}(k_{1},k_{2})|^{2}=\left(\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}\left(\mathop{\sum }_{i=1}^{N}\mathop{\sum }_{j=1}^{N}\cos (k_{1}(x_{i}-x_{j})+k_{2}(y_{i}-y_{j}))\right). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\widehat{g}(k_{1},k_{2})|^{2}=\left(\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}\left(\mathop{\sum }_{i=1}^{N}\mathop{\sum }_{j=1}^{N}\cos (k_{1}(x_{i}-x_{j})+k_{2}(y_{i}-y_{j}))\right). & & \displaystyle\end{eqnarray}$$
3.4 Discussion
The manipulation of the wind farm frequency spectrum by the sparse sampling of the turbulent boundary layer can be better understood by considering the simplified transfer function for a single streamwise column of wind turbines. For such an array of
![]() $N$
wind turbines with uniform streamwise spacing
$N$
wind turbines with uniform streamwise spacing
![]() $S_{x}$
, the transfer function is (see appendix B for details):
$S_{x}$
, the transfer function is (see appendix B for details):
 $$\begin{eqnarray}\displaystyle |\widehat{g}(k_{1},k_{2})|^{2}=\underbrace{\left(\frac{\sin \left(\displaystyle \frac{k_{1}S_{x}N}{2}\right)}{\sin \left(\displaystyle \frac{k_{1}S_{x}}{2}\right)}\right)^{2}}_{\widehat{g}_{A}(k_{1})}\underbrace{\left(\displaystyle \frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}}_{\widehat{g}_{B}(k_{2})}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\widehat{g}(k_{1},k_{2})|^{2}=\underbrace{\left(\frac{\sin \left(\displaystyle \frac{k_{1}S_{x}N}{2}\right)}{\sin \left(\displaystyle \frac{k_{1}S_{x}}{2}\right)}\right)^{2}}_{\widehat{g}_{A}(k_{1})}\underbrace{\left(\displaystyle \frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}}_{\widehat{g}_{B}(k_{2})}. & & \displaystyle\end{eqnarray}$$
The transfer function is separable in the streamwise and spanwise directions, with both components shown in figure 3. The streamwise contribution
![]() $\widehat{g}_{A}(k_{1})$
shows a power law decrease of the amplitudes for reduced wavenumbers of
$\widehat{g}_{A}(k_{1})$
shows a power law decrease of the amplitudes for reduced wavenumbers of
![]() $kS_{x}/(2\unicode[STIX]{x03C0})<1$
and peaks with amplitude
$kS_{x}/(2\unicode[STIX]{x03C0})<1$
and peaks with amplitude
![]() $N^{2}$
at increments
$N^{2}$
at increments
![]() $kS_{x}/(2\unicode[STIX]{x03C0})=0,1,2,\ldots$
of the streamwise spacing. The spanwise contribution
$kS_{x}/(2\unicode[STIX]{x03C0})=0,1,2,\ldots$
of the streamwise spacing. The spanwise contribution
![]() $\widehat{g}_{B}(k_{2})$
, shown in red, represents the averaging over the rotor width. Because this only influences scales significantly smaller than
$\widehat{g}_{B}(k_{2})$
, shown in red, represents the averaging over the rotor width. Because this only influences scales significantly smaller than
![]() $S_{x}$
, with a comparably smaller energy, the effect of
$S_{x}$
, with a comparably smaller energy, the effect of
![]() $\widehat{g}_{B}(k_{2})$
is not considered in the next part of this discussion. Doing so, the filtering is a function of
$\widehat{g}_{B}(k_{2})$
is not considered in the next part of this discussion. Doing so, the filtering is a function of
![]() $k_{1}$
only, and is given by
$k_{1}$
only, and is given by
![]() $\widetilde{E}_{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D714})=\int \widehat{g}_{A}(k_{1})E_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})\,\text{d}k_{1}$
.
$\widetilde{E}_{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D714})=\int \widehat{g}_{A}(k_{1})E_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})\,\text{d}k_{1}$
.
If the flow would stay perfectly correlated, while being advected by the mean horizontal velocity
![]() $U$
, the wavenumber–frequency spectrum would be given by
$U$
, the wavenumber–frequency spectrum would be given by
![]() $E_{k\unicode[STIX]{x1D714}}=E_{k}(k_{1})\unicode[STIX]{x1D6FF}(k_{1}-\unicode[STIX]{x1D714}/U_{1})$
, representing a Doppler shift. In this case, the filtered frequency spectrum is given by
$E_{k\unicode[STIX]{x1D714}}=E_{k}(k_{1})\unicode[STIX]{x1D6FF}(k_{1}-\unicode[STIX]{x1D714}/U_{1})$
, representing a Doppler shift. In this case, the filtered frequency spectrum is given by
![]() $\widetilde{E}_{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D714})=\widehat{g}_{A}(\unicode[STIX]{x1D714}/U_{1})E_{k}(\unicode[STIX]{x1D714}/U_{1})$
. The transfer function then directly modulates the resulting frequency spectrum, thereby extending and/or steepening the already present power-law region of the velocity spectrum and introducing peaks at frequencies corresponding to the travel time between rows of turbines. Interestingly, as shown in figure 3, the power-law range of the transfer function has a slope close to
$\widetilde{E}_{\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D714})=\widehat{g}_{A}(\unicode[STIX]{x1D714}/U_{1})E_{k}(\unicode[STIX]{x1D714}/U_{1})$
. The transfer function then directly modulates the resulting frequency spectrum, thereby extending and/or steepening the already present power-law region of the velocity spectrum and introducing peaks at frequencies corresponding to the travel time between rows of turbines. Interestingly, as shown in figure 3, the power-law range of the transfer function has a slope close to
![]() $-5/3$
for an aggregate over twenty rows. In the limit of large
$-5/3$
for an aggregate over twenty rows. In the limit of large
![]() $N$
and
$N$
and
![]() $k_{1}S_{x}/(2\unicode[STIX]{x03C0})\ll 1$
, the slope can be shown to reach a
$k_{1}S_{x}/(2\unicode[STIX]{x03C0})\ll 1$
, the slope can be shown to reach a
![]() $-2$
asymptote.
$-2$
asymptote.
In practice there is temporal decorrelation of the turbulence, which is here modelled in the wavenumber–frequency model by considering random sweeping (Wilczek et al.
Reference Wilczek, Stevens and Meneveau2015a
). The impact on
![]() $E_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})$
is depicted in figure 2(b) and figure 4 by the Doppler broadening (i.e. a broader distribution of the spectral energy) along the Doppler shift (as described by
$E_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})$
is depicted in figure 2(b) and figure 4 by the Doppler broadening (i.e. a broader distribution of the spectral energy) along the Doppler shift (as described by
![]() $\unicode[STIX]{x1D6FF}(k_{1}-\unicode[STIX]{x1D714}/U_{1})$
). Consequently, the spectral energy content of a single frequency has contributions from a range of wavenumbers. The influence on the spatially sampled frequency spectrum is visualized in figure 4. Two cuts of
$\unicode[STIX]{x1D6FF}(k_{1}-\unicode[STIX]{x1D714}/U_{1})$
). Consequently, the spectral energy content of a single frequency has contributions from a range of wavenumbers. The influence on the spatially sampled frequency spectrum is visualized in figure 4. Two cuts of
![]() $E_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})$
are shown, together with the streamwise transfer function for a wind farm with twenty rows. Due to the Doppler broadening, the sharp features from the transfer function smear out. More specifically, it widens and reduces the amplitude of the peak, and smooths out the power-law region of the transfer function.
$E_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})$
are shown, together with the streamwise transfer function for a wind farm with twenty rows. Due to the Doppler broadening, the sharp features from the transfer function smear out. More specifically, it widens and reduces the amplitude of the peak, and smooths out the power-law region of the transfer function.

Figure 3. Spatial sampling transfer functions for a single streamwise column of
![]() $N$
wind turbines, spaced evenly with spacing
$N$
wind turbines, spaced evenly with spacing
![]() $S_{x}$
and with diameter
$S_{x}$
and with diameter
![]() $D$
. The lines for
$D$
. The lines for
![]() ${\hat{g}}_{A}(k_{1})$
show lobes beginning at decreasing wavenumber as
${\hat{g}}_{A}(k_{1})$
show lobes beginning at decreasing wavenumber as
![]() $N$
increases from 10 to 200. The line for
$N$
increases from 10 to 200. The line for
![]() ${\hat{g}}_{B}(k_{2})$
(red) does not display low-wavenumber lobes below
${\hat{g}}_{B}(k_{2})$
(red) does not display low-wavenumber lobes below
![]() $k_{2}S_{x}/(2\unicode[STIX]{x03C0})\sim S_{x}/D$
.
$k_{2}S_{x}/(2\unicode[STIX]{x03C0})\sim S_{x}/D$
.

Figure 4. Comparison of two cuts of the wavenumber–frequency spectrum
![]() $E_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})$
from figure 2 with the streamwise transfer function
$E_{k\unicode[STIX]{x1D714}}(k_{1},\unicode[STIX]{x1D714})$
from figure 2 with the streamwise transfer function
![]() $\widehat{g}_{A}(k_{1})$
for a streamwise column of twenty wind turbines, spaced evenly with a spacing
$\widehat{g}_{A}(k_{1})$
for a streamwise column of twenty wind turbines, spaced evenly with a spacing
![]() $S_{x}$
.
$S_{x}$
.
3.5 Validation with experimental data
The frequency spectrum of the wind farm power output is calculated by numerically integrating equation (3.10), making use of the modelled spectrum from § 2, and with
![]() $|\widehat{g}(k_{1},k_{2})|^{2}/N^{2}$
as the transfer function (see appendix B for an overview of the transfer functions). Dividing by
$|\widehat{g}(k_{1},k_{2})|^{2}/N^{2}$
as the transfer function (see appendix B for an overview of the transfer functions). Dividing by
![]() $N^{2}$
is done to represent the relative reduction of the spectra. Because figures 5 and 6 compare the spectra of velocity fluctuations, the surrogate power signals from the wind tunnel study are scaled with the constant
$N^{2}$
is done to represent the relative reduction of the spectra. Because figures 5 and 6 compare the spectra of velocity fluctuations, the surrogate power signals from the wind tunnel study are scaled with the constant
![]() $C_{2}=(3/2)\unicode[STIX]{x1D70C}AC_{P}\overline{\langle u\rangle }^{2}$
to represent the same units. The signals are furthermore also divided by the number of considered porous disk models
$C_{2}=(3/2)\unicode[STIX]{x1D70C}AC_{P}\overline{\langle u\rangle }^{2}$
to represent the same units. The signals are furthermore also divided by the number of considered porous disk models
![]() $N$
to represent the relative reduction in the fluctuations. Here,
$N$
to represent the relative reduction in the fluctuations. Here,
![]() $\overline{\langle u\rangle }$
is chosen as the average velocity measured by the considered porous disk models in the experiment and also used to normalize the frequency axis, as an approximation of the convection velocity in the experiment.
$\overline{\langle u\rangle }$
is chosen as the average velocity measured by the considered porous disk models in the experiment and also used to normalize the frequency axis, as an approximation of the convection velocity in the experiment.

Figure 5. Comparison of the modelled wind farm spectrum and the wind tunnel data, for which
![]() $95\,\%$
confidence bounds are displayed as estimated by the pwelch routine in Matlab™. Results are shown for an aligned layout.
$95\,\%$
confidence bounds are displayed as estimated by the pwelch routine in Matlab™. Results are shown for an aligned layout.
A comparison between the modelled wind farm spectra (dashed lines) and experimental data (solid lines) is given in figures 5 and 6. As a reference, the hot-wire spectrum (orange) and the corresponding unfiltered model spectrum (black) are also shown. On each figure, four different wind farm spectra are included, each for a different sum of wind turbine power outputs. This is indicated by the number of rows
![]() $N_{R}$
over which the aggregate is taken. In each row, the values from the three central models are measured, resulting in a total aggregate over
$N_{R}$
over which the aggregate is taken. In each row, the values from the three central models are measured, resulting in a total aggregate over
![]() $N=3N_{R}$
porous disk models. When wind tunnel results are shown for less than twenty rows, the rows are selected counting from the end of the wind farm.
$N=3N_{R}$
porous disk models. When wind tunnel results are shown for less than twenty rows, the rows are selected counting from the end of the wind farm.

Figure 6. Comparison of the modelled wind farm spectrum and the wind tunnel data, for which
![]() $95\,\%$
confidence bounds are displayed as estimated by the pwelch routine in Matlab™. Results are shown for a staggered layout.
$95\,\%$
confidence bounds are displayed as estimated by the pwelch routine in Matlab™. Results are shown for a staggered layout.
For the aligned case (figure 5), excellent agreement is observed for
![]() $N_{R}=2$
, approximately within the measurement uncertainty bounds. When more rows are considered in the aggregate, the model correctly predicts the extension of the power-law region to lower frequencies. However, the agreement weakens and the modelled slope shows deviations from the measured spectra. More specifically a bulge appears in the power-law range, which influences the local slope, and the peaks become over predicted up to
$N_{R}=2$
, approximately within the measurement uncertainty bounds. When more rows are considered in the aggregate, the model correctly predicts the extension of the power-law region to lower frequencies. However, the agreement weakens and the modelled slope shows deviations from the measured spectra. More specifically a bulge appears in the power-law range, which influences the local slope, and the peaks become over predicted up to
![]() $1.5$
times for the largest aggregate. On the other hand, the low frequency limit of the model spectrum agrees with the experimental data within the uncertainty bounds. In general, it can be seen that the two main effects observed in the literature are captured by the model: an extended power-law region to lower frequencies than observed for the unfiltered spectrum and peaks at frequencies comparable to the turbine-to-turbine convection time.
$1.5$
times for the largest aggregate. On the other hand, the low frequency limit of the model spectrum agrees with the experimental data within the uncertainty bounds. In general, it can be seen that the two main effects observed in the literature are captured by the model: an extended power-law region to lower frequencies than observed for the unfiltered spectrum and peaks at frequencies comparable to the turbine-to-turbine convection time.
For the staggered layout (figure 6), it is observed that the model correctly predicts the peaks at a lower frequency due to the larger apparent spacing between streamwise aligned turbines, and that the magnitude of the main peaks are within the uncertainty bounds. The agreement is however also not perfect. There is an underestimation of the spectrum at low frequencies up to a factor of
![]() $2$
, and the second peaks at
$2$
, and the second peaks at
![]() $\unicode[STIX]{x1D714}S_{x}/(2\unicode[STIX]{x03C0}U)=1$
are overestimated.
$\unicode[STIX]{x1D714}S_{x}/(2\unicode[STIX]{x03C0}U)=1$
are overestimated.
The differences for the aligned and staggered layout are expected to be mainly caused by the use of an approximate wavenumber–frequency model with a lower energy in the low wavenumber and frequency ranges, and which does not consider the lower velocity and increased decorrelation by the presence of the wind turbines. The largest differences are seen for the staggered layout. Because the apparent spanwise spacing is twice as small, the resulting wind farm spectrum becomes significantly more sensitive to the spanwise correlation, or in some cases anti-correlation, as observed in the experiment (Bossuyt et al. Reference Bossuyt, Howland, Meneveau and Meyers2017). This indicates that the approach can be improved by better representing the wavenumber–frequency spectrum inside the wind farm.
4 Conclusions
An analytical model for the frequency spectrum of the aggregate power output from a wind farm is presented, as function of wind farm layout and inflow turbulence properties of the wind. The calculation is performed in spectral space, based on an analytical model for the wavenumber–frequency spectrum. This approach allows us to interpret and explain the interaction between the wind turbines and the boundary layer flow as a discrete spatial sampling. More specifically, it is shown how Doppler shift and broadening smear out the sharp features of the spatial sampling transfer function. The model also reproduces the observed peak in the spectrum of a wind farm at a frequency corresponding to the convective travel time between rows, and the extended steeper decay in the spectrum. The steeper decay can be considered close to a
![]() $-5/3$
power-law region (but is not strictly such a power law), which reaches up to lower frequencies than present in the spectrum of the velocity.
$-5/3$
power-law region (but is not strictly such a power law), which reaches up to lower frequencies than present in the spectrum of the velocity.
Considering its simplifications and assumptions, the model shows good agreement with the measurement data for an aligned wind farm. For a staggered layout the model under predicts the spectrum for frequencies
![]() $fS_{x}/U<0.2$
. This is expected to be related to the imperfect modelling of the flow inside the wind farm, more specifically an underestimation of the spanwise correlation. Further improvement, by studying how the wavenumber–frequency spectrum is altered by the presence of the wind turbines, is the subject of future research.
$fS_{x}/U<0.2$
. This is expected to be related to the imperfect modelling of the flow inside the wind farm, more specifically an underestimation of the spanwise correlation. Further improvement, by studying how the wavenumber–frequency spectrum is altered by the presence of the wind turbines, is the subject of future research.
Acknowledgements
The authors would like to thank M. Wilczek for the correspondence an insightful discussions. Work is supported by ERC (grant no. 306471, the ActiveWindFarms project) and by NSF (grants CBET-113380 and OISE-1243482, the WINDINSPIRE project).
Appendix A. Definitions of spectra
In this section we give a brief overview of the used notations and main definitions of spectra, following the usual conventions in the corresponding literature (Pope Reference Pope2001; Wilczek et al. Reference Wilczek, Stevens and Meneveau2015a ).
For statistically stationary and homogeneous turbulence, the wavenumber energy spectrum is defined by the Fourier transform of
![]() $R_{11}(\boldsymbol{r},0)$
:
$R_{11}(\boldsymbol{r},0)$
:
while the energy spectrum in the wavenumber–frequency domain is defined by:
Here,
![]() $R_{11}(\boldsymbol{r},\unicode[STIX]{x1D70F})$
is the two-point and two-time velocity covariance tensor of the streamwise velocity component, defined by:
$R_{11}(\boldsymbol{r},\unicode[STIX]{x1D70F})$
is the two-point and two-time velocity covariance tensor of the streamwise velocity component, defined by:
In this paper we do not consider filtering in the vertical direction. The energy spectra in the horizontal plane are found by integrating the full energy spectra over
![]() $k_{3}$
:
$k_{3}$
:
Appendix B. Calculation of the transfer function
The transfer function is calculated by applying
![]() $2\unicode[STIX]{x03C0}$
times the Fourier transform to the physical-space sampling function, in each direction (Pope Reference Pope2001):
$2\unicode[STIX]{x03C0}$
times the Fourier transform to the physical-space sampling function, in each direction (Pope Reference Pope2001):
Inserting the sampling function
![]() $g(x,y)$
and separating the integrals leads to:
$g(x,y)$
and separating the integrals leads to:
and:
By making use of Euler’s formula for complex exponentials the exponentials can be combined:
 $$\begin{eqnarray}\displaystyle \hat{g}(k_{1},k_{2})=\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\mathop{\sum }_{i=1}^{N}\exp (-\text{i}(k_{1}x_{i}+k_{2}y_{i})). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{g}(k_{1},k_{2})=\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\mathop{\sum }_{i=1}^{N}\exp (-\text{i}(k_{1}x_{i}+k_{2}y_{i})). & & \displaystyle\end{eqnarray}$$
The transfer function for the sampling of the energy spectrum
![]() $|\widehat{g}|^{2}$
is given by:
$|\widehat{g}|^{2}$
is given by:
 $$\begin{eqnarray}\displaystyle |\widehat{g}|^{2}=\widehat{g}\widehat{g}^{\ast }=\left(\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}\left[\left(\mathop{\sum }_{i=1}^{N}\cos (k_{1}x_{i}+k_{2}y_{i})\right)^{2}+\left(\mathop{\sum }_{i=1}^{N}\sin (k_{1}x_{i}+k_{2}y_{i})\right)^{2}\right], & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\widehat{g}|^{2}=\widehat{g}\widehat{g}^{\ast }=\left(\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}\left[\left(\mathop{\sum }_{i=1}^{N}\cos (k_{1}x_{i}+k_{2}y_{i})\right)^{2}+\left(\mathop{\sum }_{i=1}^{N}\sin (k_{1}x_{i}+k_{2}y_{i})\right)^{2}\right], & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
and is equal to:
 $$\begin{eqnarray}\displaystyle |\widehat{g}|^{2} & = & \displaystyle \left(\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}\left(\mathop{\sum }_{i=1}^{N}\mathop{\sum }_{j=1}^{N} (\!\cos (k_{1}x_{i}+k_{2}y_{i})\cos (k_{1}x_{j}+k_{2}y_{j})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\sin (k_{1}x_{i}+k_{2}y_{i})\sin (k_{1}x_{j}+k_{2}y_{j})\!)\!\!\vphantom{\mathop{\sum }_{i=1}^{N}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\widehat{g}|^{2} & = & \displaystyle \left(\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}\left(\mathop{\sum }_{i=1}^{N}\mathop{\sum }_{j=1}^{N} (\!\cos (k_{1}x_{i}+k_{2}y_{i})\cos (k_{1}x_{j}+k_{2}y_{j})\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\sin (k_{1}x_{i}+k_{2}y_{i})\sin (k_{1}x_{j}+k_{2}y_{j})\!)\!\!\vphantom{\mathop{\sum }_{i=1}^{N}}\right).\end{eqnarray}$$
By making use of the trigonometric identities:
![]() $2\cos (a)\cos (b)=\cos (a-b)+\cos (a+b)$
and
$2\cos (a)\cos (b)=\cos (a-b)+\cos (a+b)$
and
![]() $2\sin (a)\sin (b)=\cos (a-b)-\cos (a+b)$
, this can be simplified to:
$2\sin (a)\sin (b)=\cos (a-b)-\cos (a+b)$
, this can be simplified to:
 $$\begin{eqnarray}\displaystyle |\widehat{g}(k_{1},k_{2})|^{2}=\left(\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}\left(\mathop{\sum }_{i=1}^{N}\mathop{\sum }_{j=1}^{N}\cos (k_{1}(x_{i}-x_{j})+k_{2}(y_{i}-y_{j}))\right). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\widehat{g}(k_{1},k_{2})|^{2}=\left(\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}\left(\mathop{\sum }_{i=1}^{N}\mathop{\sum }_{j=1}^{N}\cos (k_{1}(x_{i}-x_{j})+k_{2}(y_{i}-y_{j}))\right). & & \displaystyle\end{eqnarray}$$
For the special case of one streamwise column of
![]() $N$
wind turbines with spacing
$N$
wind turbines with spacing
![]() $S_{x}$
, the sum in (B 4) becomes the geometric series:
$S_{x}$
, the sum in (B 4) becomes the geometric series:
![]() $\sum _{n=0}^{N-1}\exp (-\text{i}nS_{x}k_{1})=(1-\exp (-\text{i}NS_{x}k_{1}))/(1-\exp (-\text{i}S_{x}k_{1}))$
so that:
$\sum _{n=0}^{N-1}\exp (-\text{i}nS_{x}k_{1})=(1-\exp (-\text{i}NS_{x}k_{1}))/(1-\exp (-\text{i}S_{x}k_{1}))$
so that:
 $$\begin{eqnarray}\displaystyle \hat{g}(k_{1},k_{2})=\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\frac{1-\exp (-\text{i}NS_{x}k_{1})}{1-\exp (-\text{i}S_{x}k_{1})}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{g}(k_{1},k_{2})=\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\frac{1-\exp (-\text{i}NS_{x}k_{1})}{1-\exp (-\text{i}S_{x}k_{1})}, & & \displaystyle\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle |\widehat{g}(k_{1},k_{2})|^{2}=\left(\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}\left(\frac{\sin \left(\displaystyle \frac{k_{1}S_{x}N}{2}\right)}{\sin \left(\displaystyle \frac{k_{1}S_{x}}{2}\right)}\right)^{2}. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\widehat{g}(k_{1},k_{2})|^{2}=\left(\frac{\sin \left(k_{2}\displaystyle \frac{D}{2}\right)}{k_{2}\displaystyle \frac{D}{2}}\right)^{2}\left(\frac{\sin \left(\displaystyle \frac{k_{1}S_{x}N}{2}\right)}{\sin \left(\displaystyle \frac{k_{1}S_{x}}{2}\right)}\right)^{2}. & & \displaystyle\end{eqnarray}$$

Figure 7. The spatial sampling transfer function
![]() $|\widehat{g}(k_{1},k_{2})|^{2}/N^{2}$
for a single streamwise column with 20 wind turbines (a), an aligned wind farm with 20 rows and 5 columns (b), a staggered wind farm with 20 rows and 5 columns (c) and the aligned wind farm rotated
$|\widehat{g}(k_{1},k_{2})|^{2}/N^{2}$
for a single streamwise column with 20 wind turbines (a), an aligned wind farm with 20 rows and 5 columns (b), a staggered wind farm with 20 rows and 5 columns (c) and the aligned wind farm rotated
![]() $45^{\circ }$
with the
$45^{\circ }$
with the
![]() $k_{1}$
direction (d).
$k_{1}$
direction (d).
Figure 7 shows the transfer function calculated with (B 7) for several cases that are representative for the experimental set-up, as described in § 2. Figure 7(a) is for a single streamwise column with 20 wind turbines, spaced evenly with
![]() $S_{x}$
. A peak at
$S_{x}$
. A peak at
![]() $k_{1}=2\unicode[STIX]{x03C0}/S_{x}$
is observed in the streamwise direction. In the spanwise direction, the box filter by the turbine diameter can be noticed. Figure 7(b) is for an aligned wind farm with 20 spanwise rows and 5 streamwise columns, spaced evenly in the streamwise direction with
$k_{1}=2\unicode[STIX]{x03C0}/S_{x}$
is observed in the streamwise direction. In the spanwise direction, the box filter by the turbine diameter can be noticed. Figure 7(b) is for an aligned wind farm with 20 spanwise rows and 5 streamwise columns, spaced evenly in the streamwise direction with
![]() $S_{x}$
and in the spanwise direction with
$S_{x}$
and in the spanwise direction with
![]() $S_{y}$
. In the spanwise direction, the filter also shows a peak at
$S_{y}$
. In the spanwise direction, the filter also shows a peak at
![]() $k_{2}=2\unicode[STIX]{x03C0}/S_{y}$
. Figure 7(c) considers a staggered wind farm by shifting the even rows with
$k_{2}=2\unicode[STIX]{x03C0}/S_{y}$
. Figure 7(c) considers a staggered wind farm by shifting the even rows with
![]() $S_{y}/2$
in the spanwise direction. The peak in the spanwise direction has now shifted to
$S_{y}/2$
in the spanwise direction. The peak in the spanwise direction has now shifted to
![]() $k_{2}=4\unicode[STIX]{x03C0}/S_{y}$
, because of the smaller apparent spanwise spacing. An extra peak is observed at
$k_{2}=4\unicode[STIX]{x03C0}/S_{y}$
, because of the smaller apparent spanwise spacing. An extra peak is observed at
![]() $k_{1}=\unicode[STIX]{x03C0}/S_{x}$
and
$k_{1}=\unicode[STIX]{x03C0}/S_{x}$
and
![]() $k_{2}=2\unicode[STIX]{x03C0}/S_{x}$
, representative for the streamwise aligned wind turbines which have now a spacing of
$k_{2}=2\unicode[STIX]{x03C0}/S_{x}$
, representative for the streamwise aligned wind turbines which have now a spacing of
![]() $2S_{x}$
. Figure 7(d) is for the aligned wind farm, angled
$2S_{x}$
. Figure 7(d) is for the aligned wind farm, angled
![]() $45^{\circ }$
compared to the
$45^{\circ }$
compared to the
![]() $k_{1}$
direction, as an example for a different wind direction.
$k_{1}$
direction, as an example for a different wind direction.