Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-29T15:17:42.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Weakly nonlinear stability analysis of polymer fibre spinning

Published online by Cambridge University Press:  08 July 2015

Karan Gupta  and
Paresh Chokshi
Karan Gupta
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Delhi, New Delhi 110016, India
Paresh Chokshi*
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Delhi, New Delhi 110016, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The extensional flow of a polymeric fluid during the fibre spinning process is studied for finite-amplitude stability behaviour. The spinning flow is assumed to be inertialess and isothermal. The nonlinear extensional rheology of the polymer is described with the help of the eXtended Pom-Pom (XXP) model, which is known to exhibit a significant strain hardening effect necessary for fibre spinning applications. The linear stability analysis predicts an instability known as draw resonance when the draw ratio, 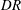$\mathit{DR}$, defined as the ratio of the velocities at the two ends of the fibre in the air gap, exceeds a certain critical value, 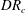$\mathit{DR}_{c}$. The critical draw ratio 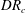$\mathit{DR}_{c}$ depends on the fluid elasticity represented by the Deborah number, 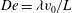$\mathit{De}={\it\lambda}v_{0}/L$, the ratio of the polymer relaxation time to the flow time scale, thus constructing a stability diagram in the 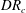$\mathit{DR}_{c}$–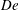$\mathit{De}$ plane. Here, 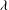${\it\lambda}$ is the characteristic relaxation time of the polymer, 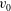$v_{0}$ is the extrudate velocity through the die exit and 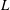$L$ is the length of the air gap for the spinning flow. In the present study, we carry out a weakly nonlinear stability analysis to examine the dynamics of the disturbance amplitude in the vicinity of the transition point. The analysis reveals the nature of the bifurcation at the transition point and constructs a finite-amplitude manifold providing insight into the draw resonance phenomena. The effect of the fluid elasticity on the nature of the bifurcation and the finite-amplitude branch is examined, and the findings are correlated to the extensional rheological behaviour of the polymer fluid. For flows at small Deborah number, the Landau constant, which captures the role of nonlinearities, is found to be negative, indicating supercritical Hopf bifurcation at the transition point. In the linearly unstable region, the equilibrium amplitude of the disturbance is estimated and shows a limit cycle behaviour. As the fluid elasticity is increased, initially the equilibrium amplitude is found to decrease below its Newtonian value, reaching the lowest value for 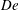$\mathit{De}$ when the strain hardening effect is maximum. With further increase in elasticity, the material undergoes strain softening behaviour which leads to an increase in the equilibrium amplitude of the oscillations in the fibre cross-section area, indicating a destabilizing effect of elasticity in this regime. Interestingly, at a certain high Deborah number, the bifurcation crosses over from supercritical to subcritical nature. In the subcritical regime, a threshold amplitude branch is constructed from the amplitude equation.

JFM classification

Instability: Nonlinear instability Non-Newtonian Flows: Non-Newtonian Flows Nonlinear Dynamical Systems: Bifurcation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 268 - 289
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auhl, D., Hoyle, D. M., Hassell, D., Lord, T. D. & Harlen, O. G. 2011 Cross-slot extensional rheometry and the steady-state extensional response of long chain branched polymer melts. J. Rheol. 55, 875–900.Google Scholar
Cao, J. 1991 Studies on the mechanism of draw resonance in melt spinning. J. Appl. Polym. Sci. 42, 143–151.Google Scholar
Cao, J. 1993 Numerical simulations of draw resonance in melt spinning of polymer fluids. J. Appl. Polym. Sci. 49, 1759–1768.Google Scholar
Chokshi, P. & Kumaran, V. 2008a Weakly nonlinear analysis of viscous instability in flow past a neo-Hookean surface. Phys. Rev. E 77, 1–15.Google Scholar
Chokshi, P. & Kumaran, V. 2008b Weakly nonlinear stability analysis of a flow past a neo-Hookean solid at arbitrary Reynolds number. Phys. Fluids 20, 094109.Google Scholar
Christenen, R. E. 1962 Extrusion coating of polypropylene. SPE J. 18, 751–755.Google Scholar
Demay, Y. & Agassant, J.-F. 1985 Experimental study of the draw resonance in fiber spinning. J. Non-Newtonian Fluid Mech. 18, 187–198.Google Scholar
Doi, M. & Edwards, S. F. 1978 Dynamics of concentrated polymer systems. J. Chem. Soc. Faraday Trans. 2 74, 1789–1832.Google Scholar
Drazin, P. & Reid, W. 2004 Hydrodynamic Stability, 2nd edn. Cambridge University Press.Google Scholar
Fisher, R. & Denn, M. 1975a Draw resonance in melt spinning. Appl. Polym. Symp. 27, 103.Google Scholar
Fisher, R. & Denn, M. 1975b Finite amplitude stability and draw resonance in isothermal melt spinning. Chem. Engng Sci. 30, 1129–1134.Google Scholar
Fisher, R. & Denn, M. 1976 A theory of isothermal melt spinning and draw resonance. AIChE J. 22, 236–246.Google Scholar
Hyun, J. 1978a Theory of draw resonance – Part 1 – Newtonian fluid. AIChE J. 24, 418–422.Google Scholar
Hyun, J. 1978b Theory of draw resonance – Part 2 – Power-law and Maxwell fluids. AIChE J. 24, 423–426.Google Scholar
Hyun, J. 1999 Draw resonance in polymer processing. Kor.-Aus. Rheol. J. 11, 279–285.Google Scholar
Jung, H. & Hyun, J. 1999 Stability of isothermal spinning of viscoelastic fluids. Korean J. Chem. E 16, 325–330.Google Scholar
Lee, J. S., Jung, H. W., Hyun, J. C. & Scriven, L. E. 2005 Simple indicator of draw resonance instability in melt spinning processes. AIChE J. 51, 2869–2874.Google Scholar
Likhtman, A. & Ramirez, J.2009 REPTATE. http://reptate.com.Google Scholar
Matovich, M. A. & Pearson, J. R. A. 1969 Spinning a molten threadline – steady-state isothermal viscous flows. Ind. Engng Chem. Fundam. 8, 512–520.Google Scholar
Pearson, J. R. A. & Matovich, M. A. 1969 Spinning a molten threadline – stability. Ind. Engng Chem. Fundam. 8, 605–609.Google Scholar
Petrie, C. & Denn, M. 1976 Instabilities in polymer processing. AIChE J. 22, 209–236.Google Scholar
Renardy, M. 2007 Draw resonance revisited. J. Phys.: Conf. Ser. 64, 012016.Google Scholar
Reynolds, W. C. & Potter, M. C. 1967 Finite-amplitude instability of parallel shear flows. J. Fluid Mech. 27, 465–492.Google Scholar
Schultz, W. W., Zebib, A., Davis, S. H. & Lee, Y. 1984 Nonlinear stability of Newtonian fibres. J. Fluid Mech. 149, 455–475.Google Scholar
Shukla, P. & Alam, M. 2011 Weakly nonlinear theory of shear-banding instability in a granular plane Couette flow: analytical solution, comparison with numerics and bifurcation. J. Fluid Mech. 666, 204–253.Google Scholar
Stuart, J. 1956 On the effects of the Reynold’s stress on hydrodynamic stability. Z. Angew. Math. Mech. 36, S32–S38.Google Scholar
Stuart, J. 1958 On the non-linear mechanics of hydrodynamic stability. J. Fluid Mech. 4, 1–21.Google Scholar
Verbeeten, W. M. H., Peters, G. W. M. & Baaijens, F. P. T. 2001 Differential constitutive equations for polymer melts: the extended pompom model. J. Rheol. 45, 823–843.Google Scholar
van der Walt, C., Hulsen, M. A., Bogaerds, A. C. B., Meijer, H. E. H. & Bulters, M. 2012 Stability of fiber spinning under filament pull-out conditions. J. Non-Newtonian Fluid Mech. 175–176, 25–37.Google Scholar
Yun, J. H., Shin, D. M., Lee, J. S., Jung, H. W. & Hyun, J. C. 2008 Direct calculation of limit cycles of draw resonance and their stability in spinning process. J. Soc. Rheol. 36, 133–136.Google Scholar
Supplementary material: File

Gupta and Chokshi supplementary material

Gupta and Chokshi supplementary material 1

Download Gupta and Chokshi supplementary material(File)
File 54.5 KB