Hostname: page-component-6dbcb7884d-fw45b Total loading time: 0 Render date: 2025-02-14T06:30:27.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Weakly nonlinear mode interactions in spherical Rayleigh–Bénard convection

Published online by Cambridge University Press:  09 July 2019

P. M. Mannix Open the ORCID record for P. M. Mannix [Opens in a new window]  and
A. J. Mestel Open the ORCID record for A. J. Mestel [Opens in a new window]
P. M. Mannix*
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
A. J. Mestel
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In an annular spherical domain with separation 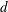$d$, the onset of convective motion occurs at a critical Rayleigh number 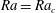$Ra=Ra_{c}$. Solving the axisymmetric linear stability problem shows that degenerate points 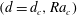$(d=d_{c},Ra_{c})$ exist where two modes simultaneously become unstable. Considering the weakly nonlinear evolution of these two modes, it is found that spatial resonances play a crucial role in determining the preferred convection pattern for neighbouring modes $(\ell ,\ell \pm 1)$ and non-neighbouring even modes 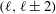$(\ell ,\ell \pm 2)$. Deriving coupled amplitude equations relevant to all degeneracies, we outline the possible solutions and the influence of changes in 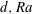$d,Ra$ and Prandtl number 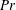$Pr$. Using direct numerical simulation (DNS) to verify all results, time periodic solutions are also outlined for small $Pr$. The 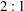$2:1$ periodic signature observed to be general for oscillations in a spherical annulus is explained using the structure of the equations. The relevance of all solutions presented is determined by computing their stability with respect to non-axisymmetric perturbations at large $Pr$.

JFM classification

Instability: Absolute/convective instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 359 - 390
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Araki, K., Mizushima, J. & Yanase, S. 1994 Thermal instability of a fluid in a spherical shell with thin layer approximation analysis. J. Phys. Soc. Japan 63 (6), 2123–2132.Google Scholar
Beltrame, P. & Chossat, P. 2015 Onset of intermittent octahedral patterns in spherical Bénard convection. Eur. J. Mech. (B/Fluids) 50, 156–174.Google Scholar
Bercovici, D., Schubert, G. & Glatzmaier, G. A. 1989 Three-dimensional spherical models of convection in the Earth’s mantle. Science 244 (4907), 950–955.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32 (1), 709–778.Google Scholar
Busse, F. H. 1975 Patterns of convection in spherical shells. J. Fluid Mech. 72 (1), 67–85.Google Scholar
Busse, F. H. & Riahi, H. 1982 Patterns of convection in spherical shells. Part 2. J. Fluid Mech. 123, 283–301.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability, International Series of Monographs on Physics, vol. 1. Clarendon.Google Scholar
Chossat, P. 1978 Bifurcation and stability of convective flows in a rotating or not rotating spherical shell. SIAM J. Appl. Maths 37 (3), 624–647.Google Scholar
Chossat, P. 2001 The bifurcation of heteroclinic cycles in systems of hydrodynamical type. J. Continuous Discrete and Impulsive Systems Series A 8 (4a), 575–590.Google Scholar
Chossat, P. & Stewart, C. A. 1992 Spherical symmetry-breaking bifurcations and thermal convection in the earth’s mantle. In Chaotic Processes in the Geological Sciences (ed. Yuen, D. A.), pp. 11–42. Springer.Google Scholar
Cox, S. M. 1996 Mode interactions in Rayleigh–Bénard convection. Physica D 95 (1), 50–61.Google Scholar
Dangelmayr, G. 1986 Steady-state mode interactions in the presence of 0(2)-symmetry. Dyn. Stab. Syst. 1, 159–185.Google Scholar
Ermentrout, B. 2002 Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students, ch. 7. SIAM.Google Scholar
Feudel, F., Bergemann, K., Tuckerman, L. S., Egbers, C., Futterer, B., Gellert, M. & Hollerbach, R. 2011 Convection patterns in a spherical fluid shell. Phys. Rev. E 83, 046304.Google Scholar
Friedrich, R. & Haken, H. 1986 Static, wavelike, and chaotic thermal convection in spherical geometries. Phys. Rev. A 34, 2100–2120.Google Scholar
Futterer, B., Egbers, C., Dahley, N., Koch, S. & Jehring, L. 2010 First identification of sub- and supercritical convection patterns from geoflow, the geophysical flow simulation experiment integrated in fluid science laboratory. Acta Astron. 66 (1), 193–200.Google Scholar
Gettling, A. V. 1998 Rayleigh–Bénard Convection: Structures and Dynamics, Advanced Series in Nonlinear Dynamics, vol. 11. World Scientific.Google Scholar
Hoyle, R. 2006 Pattern Formation: An Introduction to Methods. Cambridge University Press.Google Scholar
Jones, C. A. & Moore, D. R. 1978 The stability of axisymmetric convection. Geophys. Astrophys. Fluid Dyn. 11 (1), 245–270.Google Scholar
Joseph, D. D. & Carmi, S. 1966 Subcritical convective instability. Part 2. Spherical shells. J. Fluid Mech. 26 (4), 769–777.Google Scholar
Kidachi, H. 1982 Side wall effect on the pattern formation of the Rayleigh–Bénard convection. Prog. Theor. Phys. 68 (1), 49–63.Google Scholar
Knobloch, E. & Guckenheimer, J. 1983 Convective transitions induced by a varying aspect ratio. Phys. Rev. A 27, 408–417.Google Scholar
Knobloch, E. & Proctor, M. R. E. 1988 The double Hopf bifurcation with 2 : 1 resonance. Proc. R. Soc. Lond. A 415 (1848), 61–90.Google Scholar
Kuznetsov, Y. A. 2004 Elements of Applied Bifurcation Theory, 3rd edn. Applied Mathematical Sciences, vol. 112. Springer.Google Scholar
Li, L., Zhang, P., Liao, X. & Zhang, K. 2005 Multiplicity of nonlinear thermal convection in a spherical shell. Phys. Rev. E 71, 016301.Google Scholar
Mercader, I., Prat, J. & Knobloch, E. 2001 The 1:2 mode interaction in Rayleigh–Bénard convection with weakly broken midplane symmetry. Intl J. Bifurcation Chaos 11 (01), 27–41.Google Scholar
Mercader, I., Prat, J. & Knobloch, E. 2002 Robust heteroclinic cycles in two-dimensional Rayleigh–Bénard convection without boussinesq symmetry. Intl J. Bifurcation Chaos 12 (11), 2501–2522.Google Scholar
Proctor, M. R. E. & Jones, C. A. 1988 The interaction of two spatially resonant patterns in thermal convection. Part 1. Exact 1:2 resonance. J. Fluid Mech. 188, 301–335.Google Scholar
Rayleigh 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 32 (192), 529–546.Google Scholar
Schubert, G., Stevenson, D. J. & Ellsworth, K. 1981 Internal structures of the Galilean satellites. Icarus 47 (1), 46–59.Google Scholar
Thompson, M. J., Christensen-Dalsgaard, J., Miesch, M. S. & Toomre, J. 2003 The internal rotation of the sun. Annu. Rev. Astron. Astrophys. 41 (1), 599–643.Google Scholar
Young, R. E. 1974 Finite-amplitude thermal convection in a spherical shell. J. Fluid Mech. 63 (4), 695–721.Google Scholar
Zebib, A., Schubert, G., Dein, J. L. & Paliwal, R. C. 1983 Character and stability of axisymmetric thermal convection in spheres and spherical shells. Geophys. Astrophys. Fluid Dyn. 23 (1), 1–42.Google Scholar
Zebib, A., Schubert, G. & Straus, J. M. 1980 Infinite Prandtl number thermal convection in a spherical shell. J. Fluid Mech. 97 (2), 257–277.Google Scholar

Mannix and Mestel supplementary movie 1

DNS of the odd-odd $\ell=1, m=3$ periodic solution for $\mathrm{Ra}_c = 440.852, \epsilon =5.85$ and $\Pran = 0.05$. Even and odd mode components of the solution oscillate with their frequencies in a $2:1$ ratio.

Download Mannix and Mestel supplementary movie 1(Video)
Video 1.4 MB

Mannix and Mestel supplementary movie 2

DNS of the even-even $\ell=2, m=4$ periodic solution for $\mathrm{Ra}_c = 1515.41, \epsilon = 0.847$ and $\Pran = 0.05$. Even and odd mode components of the solution oscillate with their frequencies in a $2:1$ ratio.

Download Mannix and Mestel supplementary movie 2(Video)
Video 1.3 MB

Mannix and Mestel supplementary movie 3

DNS of the even-even $\ell=4, m=6$ periodic solution for $\mathrm{Ra}_c = 3425.94, \epsilon =0.4594$ and $\Pran = 0.05$. Even and odd mode components of the solution oscillate with their frequencies in a $2:1$ ratio.

Download Mannix and Mestel supplementary movie 3(Video)
Video 1.6 MB