Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T23:48:49.991Z Has data issue: false hasContentIssue false
  • English
  • Français

Waves in screeching jets

Published online by Cambridge University Press:  22 February 2021

Daniel Edgington-Mitchell Open the ORCID record for Daniel Edgington-Mitchell [Opens in a new window] ,
Tianye Wang ,
Petronio Nogueira Open the ORCID record for Petronio Nogueira [Opens in a new window] ,
Oliver Schmidt Open the ORCID record for Oliver Schmidt [Opens in a new window] ,
Vincent Jaunet Open the ORCID record for Vincent Jaunet [Opens in a new window] ,
Daniel Duke Open the ORCID record for Daniel Duke [Opens in a new window] ,
Peter Jordan Open the ORCID record for Peter Jordan [Opens in a new window]  and
Aaron Towne Open the ORCID record for Aaron Towne [Opens in a new window]
Daniel Edgington-Mitchell*
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC3800, Australia
Tianye Wang
Affiliation:
Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI 48109, USA
Petronio Nogueira
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC3800, Australia
Oliver Schmidt
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California San Diego, La Jolla, CA 92093, USA
Vincent Jaunet
Affiliation:
Department Fluides, Thermique, Combustion, Institut PPRIME, CNRS - Universite de Poitiers, ENSMA, UPR 3346, 86036Poitiers, France
Daniel Duke
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC3800, Australia
Peter Jordan
Affiliation:
Department Fluides, Thermique, Combustion, Institut PPRIME, CNRS - Universite de Poitiers, ENSMA, UPR 3346, 86036Poitiers, France
Aaron Towne
Affiliation:
Department of Mechanical Engineering, University of Michigan, Ann Arbor, MI 48109, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

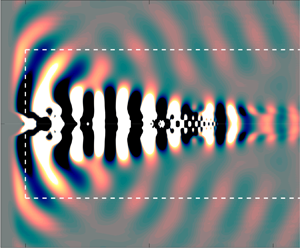
The interaction between various wave-like structures in screeching jets is considered via both experimental measurements and linear stability theory. Velocity snapshots of screeching jets are used to produce a reduced-order model of the screech cycle via proper orthogonal decomposition. Streamwise Fourier filtering is then applied to isolate the negative and positive wavenumber components, which for the waves of interest in this jet correspond to upstream- and downstream-travelling waves. A global stability analysis on an experimentally derived base flow is conducted, demonstrating a close match to the results obtained via experiment, indicating that the mechanisms considered here are well represented in a linear framework. In both the global stability analysis and the experimental decomposition, three distinct wave-like structures are evident; these waves are also solutions to the cylindrical vortex-sheet dispersion relation. One of the waves is the well-known downstream-travelling Kelvin–Helmholtz mode. Another is the upstream-travelling guided jet mode that has been a topic of recent discussion by a number of authors. The third component, with positive phase velocity, has not previously been identified in screeching jets. Via a local stability analysis, we provide evidence that this downstream-travelling wave is a duct-like mode similar to that recently identified in high-subsonic jets. We further demonstrate that both of the latter two waves are generated by the interaction between the Kelvin–Helmholtz wavepacket and the shock cells in the flow. Finally, we consider the periodic spatial modulation of the coherent velocity fluctuation evident in screeching jets, and show that this modulation can be at least partially explained by the superposition of the three wave-like structures, in addition to any possible modulation of the Kelvin–Helmholtz wavepacket by the shocks themselves.

JFM classification

Acoustics: Aeroacoustics Wakes/Jets: Jets Acoustics: Jet noise
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 913 , 25 April 2021 , A7
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Agüí, J.C. & Jimenez, J. 1987 On the performance of particle tracking. J. Fluid Mech. 185, 447–468.CrossRefGoogle Scholar
Babucke, A. 2009 Direct numerical simulation of noise-generation mechanisms in the mixing layer of a jet. PhD thesis, Universität Stuttgart.Google Scholar
Barone, M.F. & Lele, S.K. 2005 Receptivity of the compressible mixing layer. J. Fluid Mech. 540, 301–335.CrossRefGoogle Scholar
Beneddine, S., Mettot, C. & Sipp, D. 2015 Global stability analysis of underexpanded screeching jets. Eur. J. Mech. B/Fluids 49, 392–399.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J.L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.CrossRefGoogle Scholar
Berland, J., Bogey, C. & Bailly, C. 2007 Numerical study of screech generation in a planar supersonic jet. Phys. Fluids 19 (7), 075105.CrossRefGoogle Scholar
Bogey, C. & Gojon, R. 2017 Feedback loop and upwind-propagating waves in ideally expanded supersonic impinging round jets. J. Fluid Mech. 823, 562–591.CrossRefGoogle Scholar
Cavalieri, A.V., Rodríguez, D., Jordan, P., Colonius, T. & Gervais, Y. 2013 Wavepackets in the velocity field of turbulent jets. J. Fluid Mech. 730, 559–592.CrossRefGoogle Scholar
Coenen, W., Lesshafft, L., Garnaud, X. & Sevilla, A. 2017 Global instability of low-density jets. J. Fluid Mech. 820, 187–207.CrossRefGoogle Scholar
Davies, M. & Oldfield, D. 1962 Tones from a choked axisymmetric jet. Acustica 12, 257–277.Google Scholar
Deane, A., Kevrekidis, I., Karniadakis, G.E. & Orszag, S. 1991 Low-dimensional models for complex geometry flows: application to grooved channels and circular cylinders. Phys. Fluids A 3 (10), 2337–2354.CrossRefGoogle Scholar
Ducros, F., Ferrand, V., Nicoud, F., Weber, C., Darracq, D., Gacherieu, C. & Poinsot, T. 1999 Large-eddy simulation of the shock/turbulence interaction. J. Comput. Phys. 152 (2), 517–549.CrossRefGoogle Scholar
Edgington-Mitchell, D. 2019 Aeroacoustic resonance and self-excitation in screeching and impinging supersonic jets–a review. Intl J. Aeroacoust. 18 (2–3), 118–188.CrossRefGoogle Scholar
Edgington-Mitchell, D., Honnery, D.R. & Soria, J. 2014 a The underexpanded jet mach disk and its associated shear layer. Phys. Fluids 26 (9), 096101.CrossRefGoogle Scholar
Edgington-Mitchell, D., Honnery, D.R. & Soria, J. 2015 a Multimodal instability in the weakly underexpanded elliptic jet. AIAA J. 53 (9), 2739–2749.CrossRefGoogle Scholar
Edgington-Mitchell, D., Honnery, D.R. & Soria, J. 2015 b Staging behaviour in screeching elliptical jets. Intl J. Aeroacoust. 14 (7), 1005–1024.CrossRefGoogle Scholar
Edgington-Mitchell, D., Jaunet, V., Jordan, P., Towne, A., Soria, J. & Honnery, D. 2018 Upstream-travelling acoustic jet modes as a closure mechanism for screech. J. Fluid Mech. 855, R1.CrossRefGoogle Scholar
Edgington-Mitchell, D., Oberleithner, K., Honnery, D.R. & Soria, J. 2014 b Coherent structure and sound production in the helical mode of a screeching axisymmetric jet. J. Fluid Mech. 748, 822–847.CrossRefGoogle Scholar
Edgington-Mitchell, D., Weightman, J., Lock, S., Kirby, R., Nair, V., Soria, J. & Honnery, D. 2021 The generation of screech tones by shock leakage. J. Fluid Mech. 908, A46.CrossRefGoogle Scholar
Edgington-Mitchell, D.M., Duke, D., Wang, T., Harris, D., Schmidt, O.T., Jaunet, V., Jordan, P. & Towne, A. 2019 Modulation of downstream-propagating waves in aeroacoustic resonance. In 25th AIAA/CEAS Aeroacoustics Conference, p. 2689.Google Scholar
Gojon, R., Bogey, C. & Mihaescu, M. 2018 Oscillation modes in screeching jets. AIAA J. 56 (7), 2918–2924.CrossRefGoogle Scholar
Grasso, F. & Pirozzoli, S. 2000 Shock-wave–vortex interactions: shock and vortex deformations, and sound production. Theor. Comput. Fluid Dyn. 13 (6), 421–456.CrossRefGoogle Scholar
Gudmundsson, K. & Colonius, T. 2011 Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 689, 97–128.CrossRefGoogle Scholar
Hussain, A. & Reynolds, W. 1970 The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 41, 241–258.CrossRefGoogle Scholar
Jaunet, V., Collin, E. & Delville, J. 2016 Pod-galerkin advection model for convective flow: application to a flapping rectangular supersonic jet. Exp. Fluids 57 (5), 84.CrossRefGoogle Scholar
Jaunet, V., Jordan, P. & Cavalieri, A. 2017 Two-point coherence of wave packets in turbulent jets. Phys. Rev. Fluids 2 (2), 024604.CrossRefGoogle Scholar
Jaunet, V., Mancinelli, M., Jordan, P., Towne, A., Edgington-Mitchell, D.M., Lehnasch, G. & Girard, S. 2019 Dynamics of round jet impingement. In 25th AIAA/CEAS Aeroacoustics Conference, p. 2769.Google Scholar
Jordan, P. & Colonius, T. 2013 Wave packets and turbulent jet noise. Annu. Rev. Fluid Mech. 45, 173–195.CrossRefGoogle Scholar
Jordan, P., Jaunet, V., Towne, A., Cavalieri, A.V., Colonius, T., Schmidt, O. & Agarwal, A. 2018 Jet–flap interaction tones. J. Fluid Mech. 853, 333–358.CrossRefGoogle Scholar
Karami, S., Stegeman, P.C., Ooi, A., Theofilis, V. & Soria, J. 2020 Receptivity characteristics of under-expanded supersonic impinging jets. J. Fluid Mech. 889, A27.CrossRefGoogle Scholar
Li, X., He, F., Zhang, X., Hao, P. & Yao, Z. 2019 Shock motion and flow structure of an underexpanded jet in the helical mode. AIAA J. 57 (9), 3943–3953.CrossRefGoogle Scholar
Li, X.-R., Zhang, X.-W., Hao, P.-F. & He, F. 2020 Acoustic feedback loops for screech tones of underexpanded free round jets at different modes. J. Fluid Mech. 902, A17.CrossRefGoogle Scholar
Mancinelli, M., Jaunet, V., Jordan, P. & Towne, A. 2019 a Screech-tone prediction using upstream-travelling jet modes. Exp. Fluids 60 (1), 22.CrossRefGoogle Scholar
Mancinelli, M., Jaunet, V., Jordan, P., Towne, A. & Girard, S. 2019 b Reflection coefficients and screech-tone prediction in supersonic jets. In 25th AIAA/CEAS Aeroacoustics Conference, p. 2522.Google Scholar
Manning, T. & Lele, S. 2000 A numerical investigation of sound generation in supersonic jet screech. In 21st AIAA Aeroacoustics Conference.CrossRefGoogle Scholar
Martini, E., Cavalieri, A.V. & Jordan, P. 2019 Acoustic modes in jet and wake stability. J. Fluid Mech. 867, 804–834.CrossRefGoogle Scholar
Mercier, B., Castelain, T. & Bailly, C. 2017 Experimental characterisation of the screech feedback loop in underexpanded round jets. J. Fluid Mech. 824, 202–229.CrossRefGoogle Scholar
Michalke, A. 1984 Survey on jet instability theory. Prog. Aerosp. Sci. 21, 159–199.CrossRefGoogle Scholar
Mitchell, D.M., Honnery, D.R. & Soria, J. 2012 The visualization of the acoustic feedback loop in impinging underexpanded supersonic jet flows using ultra-high frame rate schlieren. J. Vis. (Visualization) 15 (4), 333–341.CrossRefGoogle Scholar
Mitchell, D.M., Honnery, D.R. & Soria, J. 2013 Near-field structure of underexpanded elliptic jets. Exp. Fluids 54 (7), 1578.CrossRefGoogle Scholar
Moreno, D., Krothapalli, A., Alkislar, M. & Lourenco, L. 2004 Low-dimensional model of a supersonic rectangular jet. Phys. Rev. E 69 (2), 026304.CrossRefGoogle ScholarPubMed
Morris, P.J. 2010 The instability of high speed jets. Intl J. Aeroacoust. 9 (1), 1–50.CrossRefGoogle Scholar
Nichols, J.W. & Lele, S.K. 2011 Global modes and transient response of a cold supersonic jet. J. Fluid Mech. 669, 225–241.CrossRefGoogle Scholar
Noack, B.R., Afanasiev, K., Morzyński, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.CrossRefGoogle Scholar
Norum, T.D. & Seiner, J.M. 1982 Measurements of mean static pressure and far field acoustics of shock containing supersonic jets. NASA-TM-84521.Google Scholar
Oberleithner, K., Sieber, M., Nayeri, C., Paschereit, C., Petz, C., Hege, H.-C., Noack, B. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.CrossRefGoogle Scholar
Oertel, H. 1980 Mach wave radiation of hot supersonic jets investigated by means of a shock tube and new optical techniques. In Proceedings of the 12th International Symposium on Shock-Tubes and Waves, Israel.Google Scholar
Pack, D. 1950 A note on prandtl's formula for the wave-length of a supersonic gas jet. Q. J. Mech. Appl. Maths 3 (2), 173–181.CrossRefGoogle Scholar
Panda, J. 1999 An experimental investigation of screech noise generation. J. Fluid Mech. 378, 71–96.CrossRefGoogle Scholar
Pickering, E., Rigas, G., Schmidt, O.T., Sipp, D. & Colonius, T. 2020 Optimal eddy viscosity for resolvent-based models of coherent structures in turbulent jets. arXiv:2005.10964 under consideration for publication in J. Fluid Mech.CrossRefGoogle Scholar
Powell, A. 1953 On the mechanism of choked jet noise. Proc. Phys. Soc. 66, 1039–1056.CrossRefGoogle Scholar
Powell, A., Umeda, Y. & Ishii, R. 1992 Observations of the oscillation modes of choked circular jets. J. Acoust. Soc. Am. 92 (5), 2823–2836.CrossRefGoogle Scholar
Prandtl, L. 1904 Über die stationären Wellen in einem Gasstrahl. Hirzel.Google Scholar
Raman, G. 1997 Cessation of screech in underexpanded jets. J. Fluid Mech. 336, 69–90.CrossRefGoogle Scholar
Ray, P. & Lele, S. 2007 Sound generated by instability wave/shock-cell interaction in supersonic jets. J. Fluid Mech. 587, 173–215.CrossRefGoogle Scholar
Schmidt, O.T., Towne, A., Colonius, T., Cavalieri, A.V., Jordan, P. & Brès, G.A. 2017 Wavepackets and trapped acoustic modes in a turbulent jet: coherent structure eduction and global stability. J. Fluid Mech. 825, 1153–1181.CrossRefGoogle Scholar
Schmidt, O.T., Towne, A., Rigas, G., Colonius, T. & Brès, G.A. 2018 Spectral analysis of jet turbulence. J. Fluid Mech. 855, 953–982.CrossRefGoogle Scholar
Shariff, K. & Manning, T.A. 2013 A ray tracing study of shock leakage in a model supersonic jet. Phys. Fluids (1994-present) 25 (7), 076103.CrossRefGoogle Scholar
Shen, H. & Tam, C. 2002 Three-dimensional numerical simulation of the jet screech phenomenon. AIAA J. 40, 33–41.CrossRefGoogle Scholar
Sinha, A., Rodríguez, D., Brès, G.A. & Colonius, T. 2014 Wavepacket models for supersonic jet noise. J. Fluid Mech. 742, 71–95.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Maths 45 (3), 561–571.CrossRefGoogle Scholar
Soria, J. 1996 An investigation of the near wake of a circular cylinder using a video-based digital cross-correlation particle image velocimetry technique. Exp. Therm. Fluid Sci. 12, 221–233.CrossRefGoogle Scholar
Suzuki, T. & Lele, S.K. 2003 Shock leakage through an unsteady vortex-laden mixing layer: application to jet screech. J. Fluid Mech. 490, 139–167.CrossRefGoogle Scholar
Taira, K., Brunton, S.L., Dawson, S.T., Rowley, C.W., Colonius, T., McKeon, B.J., Schmidt, O.T., Gordeyev, S., Theofilis, V. & Ukeiley, L.S. 2017 Modal analysis of fluid flows: an overview. AIAA J. 55 (12), 4013–4041.CrossRefGoogle Scholar
Tam, C. & Hu, F. 1989 a On the three families of instability waves of high-speed jets. J. Fluid Mech. 201, 447–483.CrossRefGoogle Scholar
Tam, C., Seiner, J. & Yu, J. 1986 Proposed relationship between broadband shock associated noise and screech tones. J. Sound Vib. 110 (2), 309–321.CrossRefGoogle Scholar
Tam, C.K. & Ahuja, K. 1990 Theoretical model of discrete tone generation by impinging jets. J. Fluid Mech. 214, 67–87.CrossRefGoogle Scholar
Tam, C.K. & Hu, F.Q. 1989 b On the three families of instability waves of high-speed jets. J. Fluid Mech. 201, 447–483.CrossRefGoogle Scholar
Tam, C.K. & Tanna, H. 1982 Shock associated noise of supersonic jets from convergent-divergent nozzles. J. Sound Vib. 81 (3), 337–358.CrossRefGoogle Scholar
Tan, D., Soria, J., Honnery, D. & Edgington-Mitchell, D. 2017 Novel method for investigating broadband velocity fluctuations in axisymmetric screeching jets. AIAA J. 55 (7), 2321–2334.CrossRefGoogle Scholar
Tan, D.J., Edgington-Mitchell, D. & Honnery, D. 2015 Measurement of density in axisymmetric jets using a novel background-oriented schlieren (BOS) technique. Exp. Fluids 56 (11), 204.CrossRefGoogle Scholar
Towne, A., Cavalieri, A.V.G., Jordan, P., Colonius, T., Schmidt, O., Jaunet, V. & Brès, G. 2017 Acoustic resonance in the potential core of subsonic jets. J. Fluid Mech. 825, 1113–1152.CrossRefGoogle Scholar
Towne, A., Schmidt, O.T. & Brès, G.A. 2019 An investigation of the Mach number dependence of trapped acoustic waves in turbulent jets. In 25th AIAA/CEAS Aeroacoustics Conference.CrossRefGoogle Scholar
Towne, A., Schmidt, O.T. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.CrossRefGoogle Scholar
Towne, A.S. 2016 Advancements in jet turbulence and noise modeling: accurate one-way solutions and empirical evaluation of the nonlinear forcing of wavepackets. PhD thesis, California Institute of Technology.Google Scholar
Weightman, J.L., Amili, O., Honnery, D., Edgington-Mitchell, D. & Soria, J. 2019 Nozzle external geometry as a boundary condition for the azimuthal mode selection in an impinging underexpanded jet. J. Fluid Mech. 862, 421–448.CrossRefGoogle Scholar
Weightman, J.L., Amili, O., Honnery, D., Soria, J. & Edgington-Mitchell, D. 2017 An explanation for the phase lag in supersonic jet impingement. J. Fluid Mech. 815, R1.CrossRefGoogle Scholar
Weightman, J.L., Amili, O., Honnery, D., Soria, J. & Edgington-Mitchell, D. 2018 Signatures of shear-layer unsteadiness in proper orthogonal decomposition. Exp. Fluids 59 (12), 180.CrossRefGoogle Scholar
Westley, R. & Woolley, J. 1975 The near field sound pressures of a choked jet when oscillating in the spinning mode. In 2nd Aeroacoustics Conference, p. 479.Google Scholar
Zaman, K.Q. & Fagan, A.F. 2020 Pressure fluctuations due to trapped waves in the initial region of high-speed jets. In AIAA Aviation 2020 Forum, p. 2523.Google Scholar