Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T15:19:27.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Waves in Newton’s bucket

Published online by Cambridge University Press:  16 October 2015

J. Mougel ,
D. Fabre  and
L. Lacaze
J. Mougel*
Affiliation:
Université de Toulouse, INPT, UPS, IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, 31400 Toulouse, France
D. Fabre
Affiliation:
Université de Toulouse, INPT, UPS, IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, 31400 Toulouse, France
L. Lacaze
Affiliation:
Université de Toulouse, INPT, UPS, IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, 31400 Toulouse, France CNRS, IMFT, 31400 Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The motion of a liquid in an open cylindrical tank rotating at a constant rate around its vertical axis of symmetry, a configuration called Newton’s bucket, is investigated using a linear stability approach. This flow is shown to be affected by several families of waves, all weakly damped by viscosity. The wave families encountered correspond to: surface waves which can be driven either by gravity or centrifugal acceleration, inertial waves due to Coriolis acceleration which are singular in the inviscid limit, and Rossby waves due to height variations of the fluid layer. These waves are described in the inviscid and viscous cases by means of mathematical considerations, global stability analysis and various asymptotic methods; and their properties are investigated over a large range of parameters 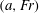$(a,Fr)$, with $a$ the aspect ratio and 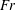$Fr$ the Froude number.

JFM classification

Vortex Flows: Vortex Flows Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 783 , 25 November 2015 , pp. 211 - 250
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. Courier Dover.Google Scholar
Bach, B., Linnartz, E. C., Vested, M. H., Andersen, A. & Bohr, T. 2014 From Newton’s bucket to rotating polygons: experiments on surface instabilities in swirling flows. J. Fluid Mech. 759, 386–403.Google Scholar
Bauer, H. F. & Eidel, W. 1997 Axisymmetric viscous liquid oscillations in a cylindrical container. Forsch. Ing. Wes. 63, 189–201.Google Scholar
Bergmann, R., Tophøj, L., Homan, T. A. M., Hersen, P., Andersen, A. & Bohr, T. 2011 Polygon formation and surface flow on a rotating fluid surface. J. Fluid Mech. 679, 415–431.Google Scholar
Borra, E. F. 1982 The liquid-mirror telescope as a viable astronomical tool. J. R. Astron. Soc. Can. 76, 245–256.Google Scholar
Eloy, C., Le Gal, P. & Le Dizès, S. 2003 Elliptic and triangular instabilities in rotating cylinders. J. Fluid Mech. 476, 357–388.Google Scholar
Fabre, D. & Mougel, J. 2014 Generation of three-dimensional patterns through wave interaction in a model of free surface swirling flow. Fluid Dyn. Res. 46 (6), 061415.CrossRefGoogle Scholar
Greenspan, H. P. 1969 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hecht, F. 2012 New development in freefem $++$ . J. Numer. Math. 20 (3–4), 251–265.Google Scholar
Henderson, D. M. & Miles, J. W. 1994 Surface-wave damping in a circular cylinder with a fixed contact line. J. Fluid Mech. 275, 285–299.CrossRefGoogle Scholar
Ibrahim, R. A. 2005 Liquid Sloshing Dynamics: Theory and Applications. Cambridge University Press.Google Scholar
Iga, K., Yokota, S., Watanabe, S., Ikeda, T., Niino, H. & Misawa, N. 2014 Various phenomena on a water vortex in a cylindrical tank over a rotating bottom. Fluid Dyn. Res. 46 (3), 031409.Google Scholar
Jansson, T. R. N., Haspang, M. P., Jensen, K. H., Hersen, P. & Bohr, T. 2006 Polygons on a rotating fluid surface. Phys. Rev. Lett. 96, 174502.Google Scholar
Jouve, L. & Ogilvie, G. I. 2014 Direct numerical simulations of an inertial wave attractor in linear and nonlinear regimes. J. Fluid Mech. 745, 223–250.Google Scholar
LeBlond, P. H. 1964 Planetary waves in a symmetrical polar basin. Tellus 16 (4), 503–512.Google Scholar
Maas, L. R. M. & Harlander, U. 2007 Equatorial wave attractors and inertial oscillations. J. Fluid Mech. 570, 47–67.Google Scholar
Manders, A. M. M. & Maas, L. R. M 2004 On the three-dimensional structure of the inertial wave field in a rectangular basin with one sloping boundary. Fluid Dyn. Res. 35, 1–21.Google Scholar
Martel, C., Nicolas, J. A. & Vega, J. M. 1998 Surface-wave damping in a brimful circular cylinder. J. Fluid Mech. 360, 213–228.Google Scholar
Miles, J. W. 1964 Free-surface oscillations in a slowly rotating liquid. J. Fluid Mech. 18 (02), 187–194.Google Scholar
Miles, J. W. & Troesh, B. A. 1961 Surface oscillations of a rotating liquid. Trans. ASME J. Appl. Mech. 28, 491–496.CrossRefGoogle Scholar
Mougel, J., Fabre, D. & Lacaze, L. 2014 Waves and instabilities in rotating free surface flows. Mech. Ind. 15, 107–112.Google Scholar
Neefe, C. W.1983 Spin casting of contact lenses. US Patent 4,416,837.Google Scholar
Newton, I. 1687 The Principia: Mathematical Principles of Natural Philosophy. University of California Press; (reprint, 1999).Google Scholar
Pedlosky, J. 1982 Geophysical Fluid Dynamics. vol. 1, p. 636. Springer.Google Scholar
Phillips, N. A. 1965 Elementary rossby waves. Tellus 17 (3), 295–301.Google Scholar
Poncet, S. & Chauve, M. P. 2007 Shear-layer instability in a rotating system. J. Flow Vis. Image Process. 14 (1).Google Scholar
Rieutord, M. & Valdettaro, L. 1997 Inertial waves in a rotating spherical shell. J. Fluid Mech. 341, 77–99.Google Scholar
Stokes, G. G. 1846 Report on recent researches in hydrodynamics. Brit. Assoc. Rep. 1, 1–20.Google Scholar
Sun, T. 1960 On fluid surface waves influenced by centrifugal force pressure. PMTPH 3, 90–96.Google Scholar
Suzuki, T., Iima, M. & Hayase, Y. 2006 Surface switching of rotating fluid in a cylinder. Phys. Fluids 18 (10), 101701.Google Scholar
Tophøj, L., Mougel, J., Bohr, T. & Fabre, D. 2013 Rotating polygon instability of a swirling free surface flow. Phys. Rev. Lett. 110 (19), 194502.Google Scholar
Ursell, F. 1952 Edge waves on a sloping beach. Proc. R. Soc. Lond. A 214 (1116), 79–97.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-scale Circulation. Cambridge University Press.CrossRefGoogle Scholar
Vatistas, G. H. 1990 A note on liquid vortex sloshing and kelvin’s equilibria. J. Fluid Mech. 217, 241–248.Google Scholar
Verfurth, R. 1991 Finite element approximation of incompressible Navier–Stokes equations with slip boundary conditions 2. Numer. Math. 59, 615–635.Google Scholar