Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-29T04:33:13.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Waves and vortices in the inverse cascade regime of stratified turbulence with or without rotation

Published online by Cambridge University Press:  30 September 2016

Corentin Herbert ,
Raffaele Marino ,
Duane Rosenberg  and
Annick Pouquet
Corentin Herbert*
Affiliation:
Department of Physics of Complex Systems, Weizmann Institute of Science, 76100 Rehovot, Israel National Center for Atmospheric Research, P.O. Box 3000, Boulder, CO 80307, USA
Raffaele Marino
Affiliation:
Laboratoire de Physique, ENS de Lyon, CNRS, Université de Lyon, F-69342 Lyon, France Laboratoire de Mécanique des Fluides et d’Acoustique, CNRS, Ecole Centrale de Lyon, Université de Lyon, F-69134 Ecully, France Dipartimento di Fisica, Università della Calabria, Ponte P. Bucci, cubo 31C, 87036 Rende, Italy
Duane Rosenberg
Affiliation:
National Center for Computational Sciences, Oak Ridge National Laboratory, P.O. Box 2008, Oak Ridge, TN 37831, USA
Annick Pouquet
Affiliation:
National Center for Atmospheric Research, P.O. Box 3000, Boulder, CO 80307, USA Laboratory for Atmospheric and Space Physics, University of Colorado, Boulder, CO 80309, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

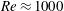We study the partition of energy between waves and vortices in stratified turbulence, with or without rotation, for a variety of parameters, focusing on the behaviour of the waves and vortices in the inverse cascade of energy towards the large scales. 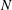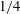To this end, we use direct numerical simulations in a cubic box at a Reynolds number $Re\approx 1000$, with the ratio between the Brunt–Väisälä frequency $N$ and the inertial frequency $f$ varying from $1/4$ to 20, together with a purely stratified run. The Froude number, measuring the strength of the stratification, varies within the range 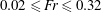$0.02\leqslant Fr\leqslant 0.32$. We find that the inverse cascade is dominated by the slow quasi-geostrophic modes. Their energy spectra and fluxes exhibit characteristics of an inverse cascade, even though their energy is not conserved. Surprisingly, the slow vortices still dominate when the ratio 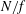$N/f$ increases, also in the stratified case, although less and less so. However, when 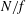$N/f$ increases, the inverse cascade of the slow modes becomes weaker and weaker, and it vanishes in the purely stratified case. We discuss how the disappearance of the inverse cascade of energy with increasing 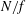$N/f$ can be interpreted in terms of the waves and vortices, and identify the main effects that can explain this transition based on both inviscid invariants arguments and viscous effects due to vertical shear.

JFM classification

Geophysical and Geological Flows: Internal waves Turbulent Flows: Rotating turbulence Turbulent Flows: Stratified turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 806 , 10 November 2016 , pp. 165 - 204
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aluie, H. & Kurien, S. 2011 Joint downscale fluxes of energy and potential enstrophy in rotating stratified Boussinesq flows. Europhys. Lett. 96 (4), 44006.Google Scholar
Babin, A., Mahalov, A., Nicolaenko, B. & Zhou, Y. 1997 On the asymptotic regimes and the strongly stratified limit of rotating Boussinesq equations. Theor. Comput. Fluid Dyn. 9, 223–251.CrossRefGoogle Scholar
Baer, F. & Tribbia, J. J. 1977 On complete filtering of gravity modes through nonlinear initialization. Mon. Weath. Rev. 105, 1536–1539.Google Scholar
Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 52, 4410–4428.2.0.CO;2>CrossRefGoogle Scholar
Bartello, P. & Tobias, S. M. 2013 Sensitivity of stratified turbulence to the buoyancy Reynolds number. J. Fluid Mech. 725, 1–22.Google Scholar
Biferale, L., Musacchio, S. & Toschi, F. 2012 Inverse energy cascade in three-dimensional isotropic turbulence. Phys. Rev. Lett. 108 (16), 164501.Google Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13 (6), 1645–1651.CrossRefGoogle Scholar
Boffetta, G. & Ecke, R. E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451.CrossRefGoogle Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J. M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Brunner-Suzuki, A.-M. E. G., Sundermeyer, M. A. & Lelong, M. P. 2014 Upscale energy transfer by the vortical mode and internal waves. J. Phys. Oceanogr. 44, 2446–2469.Google Scholar
Bühler, O., Callies, J. & Ferrari, R. 2014 Wave–vortex decomposition of one-dimensional ship-track data. J. Fluid Mech. 756, 1007–1026.Google Scholar
Callies, J., Ferrari, R. & Bühler, O. 2014 Transition from geostrophic turbulence to inertia–gravity waves in the atmospheric energy spectrum. Proc. Natl Acad. Sci. USA 111 (48), 17033–17038.Google Scholar
Campagne, A., Gallet, B., Moisy, F. & Cortet, P.-P. 2015 Disentangling inertial waves from eddy turbulence in a forced rotating-turbulence experiment. Phys. Rev. E 91 (4), 043016.Google Scholar
Celani, A., Musacchio, S. & Vincenzi, D. 2010 Turbulence in more than two and less than three dimensions. Phys. Rev. Lett. 104 (18), 184506.Google Scholar
Charney, J. G. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1094.Google Scholar
Deusebio, E., Boffetta, G., Lindborg, E. & Musacchio, S. 2014 Dimensional transition in rotating turbulence. Phys. Rev. E 90, 023005.Google Scholar
Dewan, E. M. 1979 Stratospheric wave spectra resembling turbulence. Science 204, 832–835.CrossRefGoogle ScholarPubMed
Embid, P. F. & Majda, A. J. 1998 Low Froude number limiting dynamics for stably stratified flow with small or finite Rossby numbers. Geophys. Astrophys. Fluid Dyn. 87 (1–2), 1–50.Google Scholar
Errico, R. M. 1984 The statistical equilibrium solution of a primitive-equation model. Tellus A 36 (1), 42–51.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2009 A theory of baroclinic turbulence. J. Atmos. Sci. 66, 2444–2454.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2012 Dynamics of streamwise rolls and streaks in turbulent wall-bounded shear flow. J. Fluid Mech. 708, 149–196.Google Scholar
Ferrari, R. & Wunsch, C. 2009 Ocean circulation kinetic energy: reservoirs, sources, and sinks. Annu. Rev. Fluid Mech. 41 (1), 253–282.CrossRefGoogle Scholar
Gage, K. S. 1979 Evidence for k -5/3 law inertial range in mesoscale two-dimensional turbulence. J. Atmos. Sci. 36, 1950–1954.Google Scholar
Garrett, C. & Munk, W. H. 1979 Internal waves in the ocean. Annu. Rev. Fluid Mech. 11 (1), 339–369.Google Scholar
Godeferd, F. S. & Cambon, C. 1994 Detailed investigation of energy transfers in homogeneous stratified turbulence. Phys. Fluids 6 (6), 2084–2100.Google Scholar
Godeferd, F. S. & Staquet, C. 2003 Statistical modelling and direct numerical simulations of decaying stably stratified turbulence. Part 2. Large-scale and small-scale anisotropy. J. Fluid Mech. 486, 115–159.Google Scholar
Godoy-Diana, R., Chomaz, J.-M. & Billant, P. 2004 Vertical length scale selection for pancake vortices in strongly stratified viscous fluids. J. Fluid Mech. 504, 229–238.Google Scholar
Hasselmann, K. 1966 Feynman diagrams and interaction rules of wave–wave scattering processes. Rev. Geophys. 4 (1), 1–32.Google Scholar
Herbert, C. 2014 Restricted partition functions and inverse energy cascades in parity symmetry breaking flows. Phys. Rev. E 89, 013010.Google Scholar
Herbert, C., Pouquet, A. & Marino, R. 2014 Restricted equilibrium and the energy cascade in rotating and stratified flows. J. Fluid Mech. 758, 374–406.Google Scholar
Herring, J. R. & Métais, O. 1989 Numerical experiments in forced stably stratified turbulence. J. Fluid Mech. 202 (1), 97–115.Google Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40 (1), 169–184.Google Scholar
Kartashova, E., Nazarenko, S. & Rudenko, O. 2008 Resonant interactions of nonlinear water waves in a finite basin. Phys. Rev. E 78, 016304.Google Scholar
Kimura, Y. & Herring, J. R. 2012 Energy spectra of stably stratified turbulence. J. Fluid Mech. 698, 19–50.Google Scholar
Kitamura, Y. & Matsuda, Y. 2010 Energy cascade processes in rotating stratified turbulence with application to the atmospheric mesoscale. J. Geophys. Res. 115, D11104.Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423.CrossRefGoogle Scholar
Kraichnan, R. H. & Montgomery, D. C. 1980 Two-dimensional turbulence. Rep. Prog. Phys. 43, 547.Google Scholar
Kurien, S. & Smith, L. M. 2012 Asymptotics of unit Burger number rotating and stratified flows for small aspect ratio. Physica D 241 (3), 149–163.Google Scholar
Kurien, S. & Smith, L. M. 2014 Effect of rotation and domain aspect-ratio on layer formation in strongly stratified Boussinesq flows. J. Turbul. 15 (4), 241–271.CrossRefGoogle Scholar
Laval, J.-P., Mcwilliams, J. C. & Dubrulle, B. 2003 Forced stratified turbulence: successive transitions with Reynolds number. Phys. Rev. E 68 (3), 036308.Google Scholar
Lee, T. D. 1952 On some statistical properties of hydrodynamical and magneto-hydrodynamical fields. Q. Appl. Maths 10, 69–74.CrossRefGoogle Scholar
Leith, C. E. 1980 Nonlinear normal mode initialization and quasi-geostrophic theory. J. Atmos. Sci. 37, 958–968.Google Scholar
Clark di Leoni, P. & Mininni, P. D. 2015 Absorption of waves by large-scale winds in stratified turbulence. Phys. Rev. E 91 (3), 033015.Google Scholar
Lien, R.-C. & Müller, P. 1992 Consistency relations for gravity and vortical modes in the ocean. Deep-Sea Res. 39 (9), 1595–1612.Google Scholar
Lilly, D. K. 1983 Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Sci. 40, 749–761.Google Scholar
Lilly, D. K., Bassett, G., Droegemeier, K. & Bartello, P. 1998 Stratified turbulence in the atmospheric mesoscales. Theor. Comput. Fluid Dyn. 11 (3–4), 139–153.Google Scholar
Lindborg, E. 2005 The effect of rotation on the mesoscale energy cascade in the free atmosphere. Geophys. Res. Lett. 32 (1), L01809.Google Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Lindborg, E. 2015 A Helmholtz decomposition of structure functions and spectra calculated from aircraft data. J. Fluid Mech. 762, R4.Google Scholar
Longuet-Higgins, M. S., Gill, A. E. & Kenyon, K. 1967 Resonant interactions between planetary waves. Proc. R. Soc. Lond. A 299, 120–144.Google Scholar
Marino, R., Mininni, P. D., Rosenberg, D. & Pouquet, A. 2013 Inverse cascades in rotating stratified turbulence: fast growth of large scales. Europhys. Lett. 102, 44006.CrossRefGoogle Scholar
Marino, R., Mininni, P. D., Rosenberg, D. L. & Pouquet, A. 2014 Large-scale anisotropy in stably stratified rotating flows. Phys. Rev. E 90 (2), 023018.Google Scholar
Marino, R., Pouquet, A. & Rosenberg, D. 2015 Resolving the paradox of oceanic large-scale balance and small-scale mixing. Phys. Rev. Lett. 114, 114504.Google Scholar
Mckeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.Google Scholar
Métais, O., Bartello, P., Garnier, E., Riley, J. J. & Lesieur, M. 1996 Inverse cascade in stably stratified rotating turbulence. Dyn. Atmos. Oceans 23 (1), 193–203.Google Scholar
Métais, O., Riley, J. J. & Lesieur, M. 1994 Numerical simulations of stably-stratified rotating turbulence. In Stably-Stratified Flows – Flow and Dispersion over Topography (ed. Castro, I. P. & Rockliff, N. J.), pp. 139–151. Oxford University Press.Google Scholar
Mininni, P. D. 2011 Scale interactions in magnetohydrodynamic turbulence. Annu. Rev. Fluid Mech. 43 (1), 377–397.Google Scholar
Mininni, P. D., Rosenberg, D. & Pouquet, A. 2012 Isotropization at small scales of rotating helically driven turbulence. J. Fluid Mech. 699, 263–279.Google Scholar
Mininni, P. D., Rosenberg, D., Reddy, R. & Pouquet, A. 2011 A hybrid MPI–OpenMP scheme for scalable parallel pseudospectral computations for fluid turbulence. Parallel Comput. 37, 316–326.Google Scholar
Moarref, R. & Jovanović, M. R. 2010 Controlling the onset of turbulence by streamwise travelling waves. Part 1. Receptivity analysis. J. Fluid Mech. 663, 70–99.Google Scholar
Müller, P., Holloway, G., Henyey, F. & Pomphrey, N. 1986 Nonlinear-interactions among internal gravity–waves. Rev. Geophys. 24 (3), 493–536.Google Scholar
Nastrom, G. D., Gage, K. S. & Jasperson, W. H. 1984 Kinetic energy spectrum of large-and mesoscale atmospheric processes. Nature 310, 36–38.Google Scholar
Nazarenko, S. V. 2010 Wave Turbulence, Lecture Notes in Physics, vol. 825. Springer.Google Scholar
Newell, A. C. 1969 Rossby wave packet interactions. J. Fluid Mech. 35, 255–271.CrossRefGoogle Scholar
Newell, A. C. & Rumpf, B. 2011 Wave turbulence. Annu. Rev. Fluid Mech. 43 (1), 59–78.Google Scholar
Pouquet, A. & Marino, R. 2013 Geophysical turbulence and the duality of the energy flow across scales. Phys. Rev. Lett. 111, 234501.CrossRefGoogle Scholar
Pouquet, A., Sen, A., Rosenberg, D., Mininni, P. & Baerenzung, J. 2013 Inverse cascades in turbulence and the case of rotating flows. Phys. Scr. T 155, 014032.Google Scholar
Praud, O., Fincham, A. M. & Sommeria, J. 2005 Decaying grid turbulence in a strongly stratified fluid. J. Fluid Mech. 522, 1–33.Google Scholar
Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15, 2047–2059.Google Scholar
Riley, J. J. & Lelong, M.-P. 2000 Fluid motions in the presence of strong stable stratification. Annu. Rev. Fluid Mech. 32 (1), 613–657.Google Scholar
Riley, J. J., Metcalfe, R. W. & Weissman, M. A. 1981 Direct numerical simulations of homogeneous turbulence in density-stratified fluids. In AIP Conf. Proc., vol. 76, pp. 79–112. American Institute of Physics.Google Scholar
Rorai, C., Mininni, P. D. & Pouquet, A. 2014 Turbulence comes in bursts in stably stratified flows. Phys. Rev. E 89, 043002.Google Scholar
Rosenberg, D., Pouquet, A., Marino, R. & Mininni, P. D. 2015 Evidence for Bolgiano–Obukhov scaling in rotating stratified turbulence using high-resolution direct numerical simulations. Phys. Fluids 27, 055105.Google Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.Google Scholar
Sahoo, G., Bonaccorso, F. & Biferale, L. 2015 On the role of helicity for large-and small-scales turbulent fluctuations. Phys. Rev. E 92 (5), 051002.Google Scholar
Sharma, A. S. & Mckeon, B. J. 2013 On coherent structure in wall turbulence. J. Fluid Mech. 728, 196–238.Google Scholar
Smith, L. M., Chasnov, J. R. & Waleffe, F. 1996 Crossover from two- to three-dimensional turbulence. Phys. Rev. Lett. 77 (12), 2467–2470.Google Scholar
Smith, L. M. & Waleffe, F. 2002 Generation of slow large scales in forced rotating stratified turbulence. J. Fluid Mech. 451, 145–168.Google Scholar
Smyth, W. D. & Moum, J. N. 2000a Anisotropy of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1343–1362.Google Scholar
Smyth, W. D. & Moum, J. N. 2000b Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1327–1342.Google Scholar
Sozza, A., Boffetta, G., Muratore-Ginanneschi, P. & Musacchio, S. 2015 Dimensional transition of energy cascades in stably stratified forced thin fluid layers. Phys. Fluids 27, 035112.Google Scholar
Staquet, C. & Godeferd, F. S. 1998 Statistical modelling and direct numerical simulations of decaying stably stratified turbulence. Part 1. Flow energetics. J. Fluid Mech. 360, 295–340.Google Scholar
Staquet, C. & Sommeria, J. 2002 Internal gravity waves: from instabilities to turbulence. Annu. Rev. Fluid Mech. 34 (1), 559–593.Google Scholar
Sukhatme, J. & Smith, L. M. 2008 Vortical and wave modes in 3D rotating stratified flows: random large-scale forcing. Geophys. Astrophys. Fluid Dyn. 102 (5), 437–455.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-scale Circulation. Cambridge University Press.Google Scholar
Vanneste, J. 2013 Balance and spontaneous wave generation in geophysical flows. Annu. Rev. Fluid Mech. 45, 147–172.Google Scholar
Waite, M. L. 2013 Potential enstrophy in stratified turbulence. J. Fluid Mech. 722, R4.Google Scholar
Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–308.CrossRefGoogle Scholar
Waite, M. L. & Bartello, P. 2006a Stratified turbulence generated by internal gravity waves. J. Fluid Mech. 546, 313–339.Google Scholar
Waite, M. L. & Bartello, P. 2006b The transition from geostrophic to stratified turbulence. J. Fluid Mech. 568, 89–108.Google Scholar
Warn, T. 1986 Statistical mechanical equilibria of the shallow water equations. Tellus A 38 (1), 1–11.Google Scholar
Warn, T., Bokhove, O., Shepherd, T. G. & Vallis, G. K. 1995 Rossby number expansions, slaving principles, and balance dynamics. Q. J. R. Meteorol. Soc. 121 (523), 723–739.CrossRefGoogle Scholar
Whitehead, J. P. & Wingate, B. A. 2014 The influence of fast waves and fluctuations on the evolution of the dynamics on the slow manifold. J. Fluid Mech. 757, 155–178.Google Scholar
Zakharov, V. E., Lvov, V. S. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence. Springer.Google Scholar
Zeman, O. 1994 A note on the spectra and decay of rotating homogeneous turbulence. Phys. Fluids 6, 3221–3223.Google Scholar
Zhu, J.-Z., Yang, W. & Zhu, G.-Y. 2014 On one-chiral-sector-dominated turbulence states. J. Fluid Mech. 739, 479–501.Google Scholar