Article contents
Wavelet analysis of near-field pressure fluctuations generated by a subsonic jet
Published online by Cambridge University Press: 28 March 2012
Abstract
An experimental study of the pressure field generated by a subsonic, single stream, round jet is presented. The investigation is conducted in the near-field region at subsonic Mach numbers (up to 0.9) and Reynolds numbers 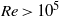 . The main task of the present work is the analysis of the near-field acoustic pressure and the characterization of its spectral properties. To this aim, a novel post-processing technique based on the application of wavelet transforms is presented. The method accomplishes the separation of nearly Gaussian background fluctuations, interpreted as acoustic pressure, from intermittent pressure peaks induced by the hydrodynamic components. With respect to more standard approaches based on Fourier filtering, the new technique permits one to recover the whole frequency content of both the acoustic and the hydrodynamic contributions and to reconstruct them as independent signals in the time domain. The near-field acoustic pressure is characterized in terms of spectral content, sound pressure level and directivity. The effects of both the Mach number and the distance from the jet axis are analysed and the results are compared with published far-field observations and theoretical predictions. Simultaneous velocity/pressure measurements have been also performed using a hot-wire probe and a microphone pair in the near field. It is shown that the cross-correlation between the near-field acoustic pressure and the axial velocity is large (of the order of 0.2) in the potential core region whereas large velocity/hydrodynamic pressure correlations are located at the nozzle exit and downstream of the potential core.
. The main task of the present work is the analysis of the near-field acoustic pressure and the characterization of its spectral properties. To this aim, a novel post-processing technique based on the application of wavelet transforms is presented. The method accomplishes the separation of nearly Gaussian background fluctuations, interpreted as acoustic pressure, from intermittent pressure peaks induced by the hydrodynamic components. With respect to more standard approaches based on Fourier filtering, the new technique permits one to recover the whole frequency content of both the acoustic and the hydrodynamic contributions and to reconstruct them as independent signals in the time domain. The near-field acoustic pressure is characterized in terms of spectral content, sound pressure level and directivity. The effects of both the Mach number and the distance from the jet axis are analysed and the results are compared with published far-field observations and theoretical predictions. Simultaneous velocity/pressure measurements have been also performed using a hot-wire probe and a microphone pair in the near field. It is shown that the cross-correlation between the near-field acoustic pressure and the axial velocity is large (of the order of 0.2) in the potential core region whereas large velocity/hydrodynamic pressure correlations are located at the nozzle exit and downstream of the potential core.
JFM classification
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 112
- Cited by


