Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-21T00:48:20.143Z Has data issue: false hasContentIssue false
  • English
  • Français

Wave packets in laminar supersonic flow over an axisymmetric compression corner

Published online by Cambridge University Press:  19 December 2024

D. Exposito Open the ORCID record for D. Exposito [Opens in a new window]
D. Exposito*
Affiliation:
Advanced Research Institute of Multidisciplinary Sciences, Beijing Institute of Technology, Beijing 100811, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

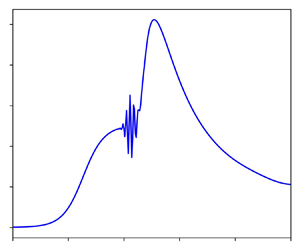
The problem of axisymmetric supersonic laminar flow separation over a compression corner has not been considered within the framework of triple-deck theory for several decades, despite significant advances in both theoretical methods and numerical techniques. In this study, we revisit the problem considered by Gittler & Kluwick (J. Fluid Mech., vol. 179, 1987, pp. 469–487), using the numerical method of Ruban (Zhurnal Vychislitel'noi Matematiki i Matematicheskoi Fiziki, vol. 18, issue 5, 1978, pp. 1253–1265) and Cassel et al. (J. Fluid Mech., vol. 300, 1995, pp. 265–285), termed the Ruban–Cassel method (RCM). The solution shows good agreement with the results of Gittler & Kluwick (J. Fluid Mech., vol. 179, 1987, pp. 469–487) for a scale external radius of 1 and scale angles from 1 to 6. However, for scale angles above 6.8, a wave packet appears. This wave packet is similar to that reported by Cassel et al. (J. Fluid Mech., vol. 300, 1995, pp. 265–285) for two-dimensional supersonic flow. As the external scale radius increases (from 1 to 10), the axisymmetric solution converges towards the two-dimensional solution for equivalent scale angle values. For a scale external radius of 10, the wave packet appears at a scale angle of 3.8, compared with the value of 3.9 by Cassel et al. (J. Fluid Mech., vol. 300, 1995, pp. 265–285). Inspection of the velocity profiles reveals that inflection points, while ubiquitous in shear flow, do not seem to play a relevant role in the appearance of the wave packet for the axisymmetric flow. Axisymmetric effects become more important as the scale external radius decreases below 0.5. A larger scale angle is necessary to produce a flow structure equivalent to that of the two-dimensional case. For scale external radius 0.1, the pressure gradient is substantially diminished and the solution is devoid of a second shear-stress minimum.

JFM classification

Aerodynamics: High-speed flow Boundary Layers: Boundary layer separation Compressible Flows: Supersonic flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1001 , 25 December 2024 , A54
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Benay, R., Chanetz, B., Mangin, B., Vandomme, L. & Perraud, J. 2006 Shock wave/transitional boundary-layer interactions in hypersonic flow. AIAA J. 44 (6), 1243–1254.CrossRefGoogle Scholar
Bodonyi, R.J., Smith, F.T. & Kluwick, A. 1985 Axisymmetric flow past a slender body of finite length. Proc. R. Soc. Lond. A 400 (1818), 37–54.Google Scholar
Broadley, H.M., Hewitt, R.E. & Gajjar, J.S.B. 2023 High-frequency instabilities in supersonic compression-ramp flow. J. Fluid Mech. 968, A5.CrossRefGoogle Scholar
Brown, L., Boyce, R., Mudford, N. & O'Byrne, S. 2009 Intrinsic three-dimensionality of laminar hypersonic shock wave/boundary layer interactions. In 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, p. 7205. AIAA.CrossRefGoogle Scholar
Brown, S.N., Stewartson, K. & Williams, P.G. 1975 Hypersonic self-induced separation. Phys. Fluids 18 (6), 633–639.CrossRefGoogle Scholar
Burggraf, O.R. & Duck, P.W. 1982 Spectral computation of triple-deck flows. In Numerical and Physical Aspects of Aerodynamic Flows (ed. T. Cebeci), pp. 145–158. Springer.CrossRefGoogle Scholar
Cassel, K.W., Ruban, A.I. & Walker, J.D.A. 1995 An instability in supersonic boundary-layer flow over a compression ramp. J. Fluid Mech. 300, 265–285.CrossRefGoogle Scholar
Exposito, D., Gai, S.L. & Neely, A.J. 2021 Wall temperature and bluntness effects on hypersonic laminar separation at a compression corner. J. Fluid Mech. 922, A1.CrossRefGoogle Scholar
Exposito, D., Gai, S.L. & Neely, A.J. 2022 A note on the appearance of wave-packets in steady-state triple-deck solutions of supersonic flow past a compression corner. J. Fluid Mech. 953, A8.CrossRefGoogle Scholar
Exposito, D., Gai, S.L. & Neely, A.J. 2023 On wave-packets and discontinuities in triple-deck solutions of supersonic separated flows at a compression corner. J. Comput. Phys. 474, 111770.CrossRefGoogle Scholar
Fletcher, A.J.P., Ruban, A.I. & Walker, J.D.A. 2004 Instabilities in supersonic compression ramp flow. J. Fluid Mech. 517, 309–330.CrossRefGoogle Scholar
Ginoux, J.J. 1971 Streamwise vortices in reattaching high-speed flows-a suggested approach. AIAA J. 9 (4), 759–760.CrossRefGoogle Scholar
Gittler, P. 1984 Laminare wechselwirkungsvorgaenge am schiebenden fluegel bei ueberschall-stroemung. Z. Angew. Math. Mech. 64, 198.Google Scholar
Gittler, P. & Kluwick, A. 1987 Triple-deck solutions for supersonic flows past flared cylinders. J. Fluid Mech. 179, 469–487.CrossRefGoogle Scholar
Hao, J., Cao, S., Wen, C.Y. & Olivier, H. 2021 Occurrence of global instability in hypersonic compression corner flow. J. Fluid Mech. 919, A4.CrossRefGoogle Scholar
Kerimbekov, R.M., Ruban, A.I. & Walker, J.D.A. 1994 Hypersonic boundary-layer separation on a cold wall. J. Fluid Mech. 274, 163–195.CrossRefGoogle Scholar
Kluwick, A., Gittler, P. & Bodonyi, R.J. 1984 Viscous-inviscid interactions on axisymmetric bodies of revolution in supersonic flow. J. Fluid Mech. 140, 281–301.CrossRefGoogle Scholar
Kluwick, A., Gittler, P. & Bodonyi, R.J. 1985 Freely interacting axisymmetric boundary layers on bodies of revolution. Q. J. Mech. Appl. Maths 38 (4), 575–588.CrossRefGoogle Scholar
Li, C. & Hao, J. 2023 Global stability of supersonic flow over a hollow cylinder/flare. J. Fluid Mech. 975, A40.CrossRefGoogle Scholar
Lighthill, M.J. 1945 Supersonic Flow Past Bodies of Revolution. HM Stationery Office.Google Scholar
Logue, R.P., Gajjar, J.S.B. & Ruban, A.I. 2014 Instability of supersonic compression ramp flow. Phil. Trans. R. Soc. A 372 (2020), 20130342.CrossRefGoogle ScholarPubMed
Lugrin, M., Beneddine, S., Leclercq, C., Garnier, E. & Bur, R. 2021 Transition scenario in hypersonic axisymmetrical compression ramp flow. J. Fluid Mech. 907, A6.CrossRefGoogle Scholar
Lugrin, M., Nicolas, F., Severac, N., Tobeli, J.P., Beneddine, S., Garnier, E., Esquieu, S. & Bur, R. 2022 Transitional shockwave/boundary layer interaction experiments in the R2CH blowdown wind tunnel. Exp. Fluids 63 (2), 46.CrossRefGoogle Scholar
Messiter, A.F. 1970 Boundary-layer flow near the trailing edge of a flat plate. SIAM J. Appl. Maths 18 (1), 241–257.CrossRefGoogle Scholar
Neiland, V.Y. 1969 Theory of laminar boundary layer separation in supersonic flow. Fluid Dyn. 4 (4), 33–35.Google Scholar
Reyhner, T.A. & Flügge-Lotz, I. 1968 The interaction of a shock wave with a laminar boundary layer. Intl J. Non-Linear Mech. 3 (2), 173–199.CrossRefGoogle Scholar
Rizzetta, D.P., Burggraf, O.R. & Jenson, R. 1978 Triple-deck solutions for viscous supersonic and hypersonic flow past corners. J. Fluid Mech. 89 (3), 535–552.CrossRefGoogle Scholar
Ruban, A.I. 1978 A numerical solution of the local asymptotic problem on the nonstationary separation of the laminar boundary layer in a supersonic flow. Zhurnal Vychislitel'noi Matematiki i Matematicheskoi Fiziki 18 (5), 1253–1265.Google Scholar
Smith, F.T. 1988 A reversed-flow singularity in interacting boundary layers. Proc. R. Soc. Lond. A 420 (1858), 21–52.Google Scholar
Smith, F.T. & Bodonyi, R.J. 1985 On short-scale inviscid instabilities in flow past surface-mounted obstacles and other non-parallel motions. Aeronaut. J. 89 (886), 205–212.CrossRefGoogle Scholar
Smith, F.T. & Khorrami, A.F. 1991 The interactive breakdown in supersonic ramp flow. J. Fluid Mech. 224, 197–215.CrossRefGoogle Scholar
Stewartson, K. 1970 On laminar boundary layers near corners. Q. J. Mech. Appl. Maths 23 (2), 137–152.CrossRefGoogle Scholar
Stewartson, K. & Williams, P.G. 1969 Self-induced separation. Proc. R. Soc. Lond. A 312 (1509), 181–206.Google Scholar
Tutty, O.R. & Cowley, S.J. 1986 On the stability and the numerical solution of the unsteady interactive boundary-layer equation. J. Fluid Mech. 168, 431–456.CrossRefGoogle Scholar
Ward, G.N. 1948 The approximate external and internal flow past a quasi-cylindrical tube moving at supersonic speeds. Q. J. Mech. Appl. Maths 1 (1), 225–245.CrossRefGoogle Scholar
Werle, M.J. & Vatsa, V.N. 1974 New method for supersonic boundary-layer separations. AIAA J. 12 (11), 1491–1497.CrossRefGoogle Scholar
Williams, P.G. 1975 A reverse flow computation in the theory of self-induced separation. In Proceedings of the Fourth International Conference on Numerical Methods in Fluid Dynamics, pp. 445–451. Springer.CrossRefGoogle Scholar