Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T02:20:26.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Water entry of rounded cylindrical bodies with different aspect ratios and surface conditions

Published online by Cambridge University Press:  28 January 2019

Nayoung Kim  and
Hyungmin Park Open the ORCID record for Hyungmin Park [Opens in a new window]
Nayoung Kim
Affiliation:
Department of Mechanical and Aerospace Engineering, Seoul National University, Seoul 08826, Korea
Hyungmin Park*
Affiliation:
Department of Mechanical and Aerospace Engineering, Seoul National University, Seoul 08826, Korea Institute of Advanced Machines and Design, Seoul National University, Seoul 08826, Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present study, we experimentally investigate water surface deformation due to the impact of rounded cylindrical projectiles with different aspect ratios (1.0–8.0). The subsequent jet and splash formation is closely related to the dynamics of an underwater cavity. To control the cavity formation, two kinds of surface conditions (smooth and rough) are applied to the front parts of the projectiles, and two impact speeds are considered. The Froude, Reynolds and Weber numbers are in the ranges of 32–90, 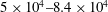$5\times 10^{4}{-}8.4\times 10^{4}$ and 1700–5000, respectively. When the front is smooth, the water film rises up along the body surface immediately after impact, and the temporal variation of its height is analytically estimated. The film converges at the rear pole to create an apex jet at lower aspect ratios and simply rises up and falls with the body at higher aspect ratios. The jets could be further distinguished as thin and thick jets, whose breakdown is found to be a function of the viscous force and surface tension, i.e. the Ohnesorge number. On the other hand, when the front is rough, the water film cannot rise up along the body surface, and instead early separation occurs to make the splash above a free surface. The splash size is quantified to assess the effects of the aspect ratio and impact speed. Upon splash formation, a cavity is created under the free surface, which emanates from the nose of the projectile. As the body sinks, the cavity pinch-off occurs due to the imbalance between the hydrostatic pressure and air pressure inside the cavity. At higher aspect ratios, cavity pinch-off occurs on the side wall of the projectile and leaves a portion of the cavity bubble on it. When the surface is smooth, no underwater cavity forms. Finally, we compare the hydrodynamic force acting on the sinking bodies with and without cavity formation, based on the underwater trajectory of each projectile. It is found that the underwater cavity reduces the drag force on the sinking body when it fully encapsulates the body; however, if the air bubbles are partially attached to the body after pinch-off, they tend to detach irregularly or impose additional drag on the body.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 757 - 788
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agüí, J. C. & Jiménez, J. 1987 On the performance of particle tracking. J. Fluid Mech. 185, 447–468.10.1017/S0022112087003252Google Scholar
Aristoff, J. M. & Bush, J. W. M. 2009 Water entry of small hydrophobic spheres. J. Fluid Mech. 619, 45–78.10.1017/S0022112008004382Google Scholar
Aristoff, J. M., Truscott, T., Techet, A. H. & Bush, J. W. M. 2010 The water entry of decelerating spheres. Phys. Fluids 22, 032102.10.1063/1.3309454Google Scholar
Benkreira, H. & Khan, M. I. 2008 Air entrainment in dip coating under reduced air pressures. Chem. Engng Sci. 63, 448–459.10.1016/j.ces.2007.09.045Google Scholar
Bodily, K. G., Carlson, S. J. & Truscott, T. T. 2014 The water entry of slender axisymmetric bodies. Phys. Fluids 26, 072108.10.1063/1.4890832Google Scholar
Chen, R. C., Yu, Y. T., Su, K. W., Chen, J. F. & Chen, Y. F. 2013 Exploration of water jet generated by Q-switched laser induced water breakdown with different depths beneath a flat free surface. Opt. Express 21, 445–453.10.1364/OE.21.000445Google Scholar
Clanet, C., Hersen, F. & Bocquet, L. 2004 Secrets of successful stone-skipping. Nature 427, 29.10.1038/427029aGoogle Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. J. Fluid Mech. 168, 169–194.10.1017/S0022112086000332Google Scholar
Das, S., Chanda, S., Eijkel, J. C. T., Tas, N. R., Chakraborty, S. & Mitra, S. K. 2014 Filling of charged cylindrical capillaries. Phy. Rev. E 90, 043011.Google Scholar
Driessen, T., Jeurissen, R., Wijshoff, H., Toschi, F. & Lohse, D. 2013 Stability of viscous long liquid filaments. Phy. Fluids 25, 062109.10.1063/1.4811849Google Scholar
Duclaux, V., Caille, F., Duez, C., Ybert, C., Bocquet, L. & Clanet, C. 2007 Dynamics of transient cavities. J. Fluid Mech. 591, 1–19.10.1017/S0022112007007343Google Scholar
Duez, C., Ybert, C., Clanet, C. & Bocquet, L. 2007 Making a splash with water repellency. Nat. Phys. 3, 180–183.10.1038/nphys545Google Scholar
Dussan, E. B. V. 1979 On the spreading of liquids on solid surfaces: static and dynamic contact lines. Annu. Rev. Fluid Mech. 11, 371–400.10.1146/annurev.fl.11.010179.002103Google Scholar
Eggers, J. & Villermaux, E. 2008 Physics of liquid jets. Rep. Prog. Phys. 71, 036601.10.1088/0034-4885/71/3/036601Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.10.1146/annurev-fluid-120710-101250Google Scholar
Gekle, S., van der Bos, A., Bergmann, R., van der Meer, D. & Lohse, D. 2008 Noncontinuous Froude number scaling for the closure depth of a cylindrical cavity. Phys. Rev. Lett. 100, 084502.10.1103/PhysRevLett.100.084502Google Scholar
Grumstrup, T., Keller, J. B. & Belmonte, A. 2007 Cavity ripples observed during the impact of solid objects into liquids. Phys. Rev. Lett. 99, 114502.10.1103/PhysRevLett.99.114502Google Scholar
Harrison, S. M., Cohen, R. C., Cleary, P. W., Barris, S. & Rose, G. 2016 A coupled biomechanical-smoothed particle hydrodynamics model for predicting the loading on the body during elite platform diving. Appl. Math. Model. 40, 3812–3831.10.1016/j.apm.2015.11.009Google Scholar
Kubiak, K. J., Wilson, M. C. T., Mathia, T. G. & Carval, P. 2011 Wettability versus roughness of engineering surfaces. Wear 271, 523–528.10.1016/j.wear.2010.03.029Google Scholar
Kubota, Y. & Mochizuki, O. 2009 Splash formation by a spherical body plunging into water. J. Vis. 12, 339–346.Google Scholar
Kubota, Y. & Mochizuki, O. 2011 Influence of head shape of solid body plunging into water on splash formation. J. Vis. 14, 111–119.Google Scholar
Kuwabara, G., Tanba, H. & Kono, K. 1987 Splash produced by a smooth sphere or circular cylinder striking a liquid surface. J. Phys. Soc. Japan 56, 2733–2743.10.1143/JPSJ.56.2733Google Scholar
Landreth, C. C. & Adrian, R. J. 1990 Impingement of a low Reynolds number turbulent circular jet onto a flat plate at normal incidence. Exp. Fluids 9, 74–84.10.1007/BF00575338Google Scholar
Latka, A., Strandburg-Peshkin, A., Driscoll, M. M., Stevens, C. S. & Nagel, S. R. 2012 Creation of prompt and thin-sheet splashing by varying surface roughness or increasing air pressure. Phys. Rev. Lett. 109, 054501.10.1103/PhysRevLett.109.054501Google Scholar
Lee, M., Longoria, R. G. & Wilson, D. E. 1997 Cavity dynamics in high-speed water entry. Phys. Fluids 9, 540–550.10.1063/1.869472Google Scholar
Mansoor, M. M., Marston, J. O., Vakarelski, I. U. & Thoroddsen, S. T. 2014 Water entry without surface seal: extended cavity formation. J. Fluid Mech. 743, 295–326.10.1017/jfm.2014.35Google Scholar
Mansoor, M. M., Vakarelski, I. U., Marston, J. O., Truscott, T. T. & Thoroddsen, S. T. 2017 Stable-streamlined and helical cavities following the impact of Leidenfrost spheres. J. Fluid Mech. 823, 716–754.10.1017/jfm.2017.337Google Scholar
Marston, J. O., Seville, J. P. K., Cheun, Y.-V., Ingram, A., Decent, S. P. & Simmons, M. J. H. 2008 Effect of packing fraction on granular jetting from solid sphere entry into aerated and fluidized beds. Phys. Fluids 20, 023301.10.1063/1.2835008Google Scholar
Marston, J. O. & Thoroddsen, S. T. 2008 Apex jets from impacting drops. J. Fluid Mech. 614, 293–302.10.1017/S0022112008003881Google Scholar
Marston, J. O., Truscott, T. T., Speirs, N. B., Mansoor, M. M. & Thoroddsen, S. T. 2016 Crown sealing and buckling instability during water entry of spheres. J. Fluid Mech. 794, 506–529.10.1017/jfm.2016.165Google Scholar
Marston, J. O., Vakarelski, I. U. & Thoroddsen, S. T. 2011 Bubble entrapment during sphere impact onto quiescent liquid surfaces. J. Fluid Mech. 680, 660–670.10.1017/jfm.2011.202Google Scholar
May, A. 1951 Effect of surface condition of a sphere on its water-entry cavity. J. Appl. Phys. 22, 1219–1222.10.1063/1.1699831Google Scholar
May, A. 1952 Vertical entry of missiles into water. J. Appl. Phys. 23, 1362–1372.10.1063/1.1702076Google Scholar
Notz, P. K. & Basaran, O. A. 2004 Dynamics and breakup of a contracting liquid filament. J. Fluid Mech. 512, 223–256.10.1017/S0022112004009759Google Scholar
Otsu, N. 1979 A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 9, 62–66.10.1109/TSMC.1979.4310076Google Scholar
Plateau, J. 1873 Experimental and Theoretical Steady State of Liquids Subjected to Nothing but Molecular Forces. Gauthiers-Villars.Google Scholar
Rayleigh, F. 1878 On the instability of jets. Proc. Lond. Math. Soc. 5, s1–10.Google Scholar
Rosellini, L., Hersen, F., Clanet, C. & Bocquet, L. 2005 Skipping stones. J. Fluid Mech. 543, 137–146.10.1017/S0022112005006373Google Scholar
Royer, J. R., Corwin, E. I., Conyers, B., Flior, A., Rivers, M. L., Eng, P. J. & Jaeger, H. M. 2008 Birth and growth of a granular jet. Phys. Rev. E 78, 011305.Google Scholar
Shepard, T., Abraham, J., Schwalbach, D., Kane, S., Siglin, D. & Harrington, T. 2014 Velocity and density effect on impact force during water entry of sphere. J. Geophys. Remote Sens. 3, 129.Google Scholar
Stone, H. A., Bentley, B. J. & Leal, L. G. 1986 An experimental study of transient effects in the breakup of viscous drops. J. Fluid Mech. 173, 131–158.10.1017/S0022112086001118Google Scholar
Sun, H. & Faltinsen, O. M. 2006 Water impact of horizontal circular cylinders and cylindrical shells. Appl. Ocean Res. 28, 299–311.10.1016/j.apor.2007.02.002Google Scholar
Thoroddsen, S. T., Etoh, T. G., Takehara, K. & Takano, Y. 2004 Impact jetting by a solid sphere. J. Fluid Mech. 499, 139–148.10.1017/S0022112003007274Google Scholar
Truscott, T. T., Epps, B. P. & Belden, J. 2014 Water entry of projectiles. Annu. Rev. Fluid Mech. 46, 355–378.10.1146/annurev-fluid-011212-140753Google Scholar
Truscott, T. T., Epps, B. P. & Techet, A. H. 2012 Unsteady forces on spheres during free-surface water entry. J. Fluid Mech. 704, 173–210.10.1017/jfm.2012.232Google Scholar
Vakarelski, I. U., Klaseboer, E., Jetly, A., Mansoor, M. M., Aguirre-Pablo, A. A., Chan, D. Y. C. & Thoroddsen, S. T. 2017 Self-determined shapes and velocities of giant near-zero drag gas cavities. Sci. Adv. 3, e1701558.10.1126/sciadv.1701558Google Scholar
Worthington, A. M. 1908 A Study of Splashes. Longmans.Google Scholar
Yao, E., Wang, H., Pan, L., Wang, X. & Woding, R. 2014 Vertical water-entry of bullet-shaped projectiles. J. Appl. Math. Phys. 2, 323–334.10.4236/jamp.2014.26039Google Scholar
Zhao, M. H., Chen, X. P. & Wang, Q. 2014 Wetting failure of hydrophilic surfaces promoted by surface roughness. Sci. Rep. 4, 5376.10.1038/srep05376Google Scholar
Zhao, R. & Faltinsen, O. 1993 Water entry of two-dimensional bodies. J. Fluid Mech. 246, 593–612.10.1017/S002211209300028XGoogle Scholar

Kim and Park supplementary movie 1

The water entry of projectiles (smooth surface) at Uo = 4.2 m/s

Download Kim and Park supplementary movie 1(Video)
Video 3.5 MB

Kim and Park supplementary movie 2

The water entry of projectiles (rough surface) at Uo = 4.2 m/s

Download Kim and Park supplementary movie 2(Video)
Video 7.4 MB

Kim and Park supplementary movie 3

The sinking behavior of body with AR 2 at Uo = 4.2 m/s

Download Kim and Park supplementary movie 3(Video)
Video 4 MB
Supplementary material: PDF

Kim and Park supplementary material

Supplementary material

Download Kim and Park supplementary material(PDF)
PDF 423.3 KB