Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Polasanapalli, Sai Ravi Gupta
and
Anupindi, Kameswararao
2024.
Turbulent mixed convection in a horizontal cylindrical cavity with the off-lattice Boltzmann method.
International Journal of Heat and Mass Transfer,
Vol. 225,
Issue. ,
p.
125395.
Zhang, Yu
Chen, Di-Lin
Luo, Xiao-Ping
Luo, Kang
Wu, Jian
and
Yi, Hong-Liang
2024.
Coulomb-driven electroconvection turbulence in two-dimensional cavity.
Journal of Fluid Mechanics,
Vol. 980,
Issue. ,
Meng, Xiaohui
Wu, Jian-Zhao
Chong, Kai Leong
and
Zhou, Quan
2024.
Heat transport and flow structure in vertical convection over rough sidewalls.
Physics of Fluids,
Vol. 36,
Issue. 10,
Huang, Ze-Lin
Wu, Jian-Zhao
Guo, Xi-Li
Zhao, Chao-Ben
Wang, Bo-Fu
Chong, Kai Leong
and
Zhou, Quan
2024.
Unifying constitutive law of vibroconvective turbulence in microgravity.
Journal of Fluid Mechanics,
Vol. 987,
Issue. ,
Zhao, Xiao-Zheng
Qiu, Can
Zhou, Sheng-Qi
Li, Yi-Zhen
Xi, Heng-Dong
and
Xia, Ke-Qing
2024.
Heat transport in three-layer turbulent thermal convection.
Physical Review Fluids,
Vol. 9,
Issue. 7,
Li, Yi-Zhen
Chen, Xin
and
Xi, Heng-Dong
2024.
Enhanced heat transfer and reduced flow reversals in turbulent thermal convection with an obstructed centre.
Journal of Fluid Mechanics,
Vol. 981,
Issue. ,
Guo, Xili
Qin, Peijiang
Wu, Jianzhao
Wang, Bofu
Chong, Kai Leong
and
Zhou, Quan
2024.
Statistics of kinetic and thermal energy dissipation rates in two-dimensional thermal vibrational convection.
Physics of Fluids,
Vol. 36,
Issue. 7,
Chong, Kai Leong
Qiao, Songniu
Wu, Jian-Zhao
and
Wang, Bo-Fu
2024.
Heat transfer enhancement in vertical convection under spatially harmonic temperature modulation.
International Journal of Heat and Mass Transfer,
Vol. 227,
Issue. ,
p.
125452.
Argade, Santosh
and
De, Ashoke
2024.
Optimization study of a Z-type airflow cooling system of a lithium-ion battery pack.
Physics of Fluids,
Vol. 36,
Issue. 6,
Xiao, Mingfei
Ren, Yangjian
Yang, Junjiao
and
Hu, Zhan-Chao
2024.
Turbulent Rayleigh–Bénard convection in a supercritical CO2-based binary mixture with cross-diffusion effects.
International Journal of Heat and Mass Transfer,
Vol. 228,
Issue. ,
p.
125648.
Yang, Wen
Deng, Pei-Yan
and
Wu, Jian-Zhao
2024.
Heat transport enhancement by rotating bottom endwall in a cylindrical Rayleigh–Bénard convection.
Physics of Fluids,
Vol. 36,
Issue. 11,
Li, Yi-Zhen
Chen, Xin
and
Xi, Heng-Dong
2024.
The large-scale circulation and temperature oscillation in turbulent thermal convection in a flattened cylindrical cell of aspect ratio 2.
Physics of Fluids,
Vol. 36,
Issue. 3,
Chen, Xin-Yuan
Yang, Juan-Cheng
and
Ni, Ming-Jiu
2024.
Effects of horizontal magnetic fields on flow morphologies and global transports in liquid metal thermal convection.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
Xu, Ao
Xu, Ben-Rui
and
Xi, Heng-Dong
2024.
Particle transport and deposition in wall-sheared thermal turbulence.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
Zhao, Hao-Bo
Zhao, Chao-Ben
Zhou, Quan
and
Chong, Kai Leong
2024.
Thermal convection modulated by actively oscillating filament: The effect of filament rigidity.
International Journal of Heat and Mass Transfer,
Vol. 228,
Issue. ,
p.
125649.
Xu, Ao
and
Li, Bo-Tao
2024.
Particle-resolved thermal lattice Boltzmann simulation using OpenACC on multi-GPUs.
International Journal of Heat and Mass Transfer,
Vol. 218,
Issue. ,
p.
124758.
Liu, Zheheng
Jia, Pan
and
Zhong, Zheng
2025.
Prandtl number effect on heat transfer and flow structures in Rayleigh–Bénard convection modulated by an oscillatory bottom plate.
International Journal of Heat and Mass Transfer,
Vol. 236,
Issue. ,
p.
126380.
Zhang, Yang
and
Zhou, Quan
2025.
Eliminating flow reversals and enhancing heat transport in turbulent thermal convection with sinusoidally heated plates.
International Journal of Heat and Mass Transfer,
Vol. 239,
Issue. ,
p.
126560.
Pan, Ming
Shen, Lian
Zhou, Quan
and
Dong, Yuhong
2025.
Particle transport and turbulence modification in unstably stratified mixed convection within a horizontal channel.
International Journal of Heat and Mass Transfer,
Vol. 236,
Issue. ,
p.
126377.
Wang, Jin-Long
Liu, Yu-Wen
Yang, Jin-Hong
Zhang, Li-Chen
Chen, Long
and
Ni, Ming-Jiu
2025.
Study on the mechanisms of flow and heat transfer in natural convection of liquid metal under a horizontal magnetic field.
Physics of Fluids,
Vol. 37,
Issue. 3,
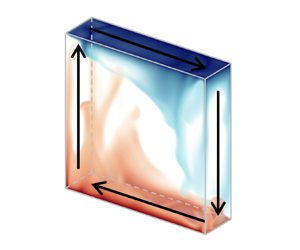
 $Ra = 10^{8}$ and fixed Prandtl number
$Ra = 10^{8}$ and fixed Prandtl number  $Pr = 5.3$, while the wall-shear Reynolds number (
$Pr = 5.3$, while the wall-shear Reynolds number ( $Re_{w}$) is in the range
$Re_{w}$) is in the range  $60 \leqslant Re_{w} \leqslant 6000$. Generally, we found enhanced heat transfer efficiency and global flow strength with the increase of
$60 \leqslant Re_{w} \leqslant 6000$. Generally, we found enhanced heat transfer efficiency and global flow strength with the increase of  $Re_{w}$. However, even with the same magnitude of global flow strength, the heat transfer efficiency varies significantly when the cells are under different types of wall shear. An interesting finding is that by increasing the wall-shear strength, the thermal turbulence is relaminarized, and more surprisingly, the heat transfer efficiency in the laminar state is higher than that in the turbulent state. We found that the enhanced heat transfer efficiency at the laminar regime is due to the formation of more stable and stronger convection channels. We propose that the origin of thermal turbulence laminarization is the reduced amount of thermal plumes. Because plumes are mainly responsible for turbulent kinetic energy production, when the detached plumes are swept away by the wall shear, the reduced number of plumes leads to weaker turbulent kinetic energy production. We also quantify the efficiency of facilitating heat transport via external shearing, and find that for larger
$Re_{w}$. However, even with the same magnitude of global flow strength, the heat transfer efficiency varies significantly when the cells are under different types of wall shear. An interesting finding is that by increasing the wall-shear strength, the thermal turbulence is relaminarized, and more surprisingly, the heat transfer efficiency in the laminar state is higher than that in the turbulent state. We found that the enhanced heat transfer efficiency at the laminar regime is due to the formation of more stable and stronger convection channels. We propose that the origin of thermal turbulence laminarization is the reduced amount of thermal plumes. Because plumes are mainly responsible for turbulent kinetic energy production, when the detached plumes are swept away by the wall shear, the reduced number of plumes leads to weaker turbulent kinetic energy production. We also quantify the efficiency of facilitating heat transport via external shearing, and find that for larger  $Re_{w}$, the enhanced heat transfer efficiency comes at a price of a larger expenditure of mechanical energy.
$Re_{w}$, the enhanced heat transfer efficiency comes at a price of a larger expenditure of mechanical energy.


