Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T06:37:01.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Wakes behind a prolate spheroid in crossflow

Published online by Cambridge University Press:  18 May 2012

George K. El Khoury ,
Helge I. Andersson  and
Bjørnar Pettersen
George K. El Khoury*
Affiliation:
Department of Marine Technology, The Norwegian University of Science and Technology, NO-7491 Trondheim, Norway
Helge I. Andersson
Affiliation:
Department of Energy and Process Engineering, The Norwegian University of Science and Technology, NO-7491 Trondheim, Norway
Bjørnar Pettersen
Affiliation:
Department of Marine Technology, The Norwegian University of Science and Technology, NO-7491 Trondheim, Norway
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Viscous laminar flow past a prolate 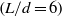spheroid has been investigated numerically at seven different Reynolds numbers; 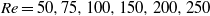and 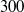. In contrast to all earlier investigations, the major axis of the spheroid was oriented perpendicular to the free stream flow. As expected, the flow field in the wake showed a strong resemblance of that observed behind a finite-length circular cylinder, yet had features observed in the axisymmetric wake behind a sphere. The following different flow regimes were observed in the present computational study: (i) steady laminar flow with massive flow separation and symmetry about the equatorial and the meridional planes at 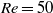; (ii) steady laminar flow with massive flow separation and symmetry about the equatorial and the meridional plane at 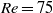, but the flow in the equatorial plane did no longer resemble the steady wake behind a circular cylinder; (iii) unsteady laminar flow with Strouhal number 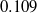and symmetry about the equatorial plane at 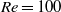; (iv) unsteady laminar flow with two distinct frequencies and without any planar symmetries at 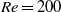; (v) transitional flow with a dominant shedding frequency 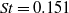and without any spatial symmetries at 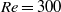. For all but the two lowest 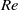hairpin vortices were alternately shed from the two sides of the spheroid and resulted in a ladder-like pattern of oppositely oriented vortex structures, in contrast with the single-sided shedding in the wake of a sphere. The contour of the very-near-wake mimicked the shape of the prolate spheroid. However, 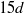downstream the major axis of the wake became aligned with the minor axis of the spheroid. This implies that an axis switching occurred some 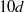downstream, i.e. the cross-section of the wake evolved such that the major and minor axes interchanged at a certain downstream location. This peculiar phenomenon has frequently been reported to arise for elliptical and rectangular jets, whereas observations of axis switching for asymmetric wakes are scarce.

JFM classification

Wakes/Jets: Separated flows Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 701 , 25 June 2012 , pp. 98 - 136
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Achenbach, E. 1974 Vortex shedding from spheres. J. Fluid Mech. 62, 209–221.CrossRefGoogle Scholar
2. Andersson, H. I., Zhao, L. & Barri, M. 2012 Torque-coupling and particle-turbulence interactions. J. Fluid Mech. 696, 319–329.CrossRefGoogle Scholar
3. Breach, D. R. 1961 Slow flow past ellipsoids of revolution. J. Fluid Mech. 10, 306–314.CrossRefGoogle Scholar
4. Brücker, C. 2001 Spatio-temporal reconstruction of vortex dynamics in axisymmetric wakes. J. Fluids Struct. 15, 543–554.CrossRefGoogle Scholar
5. Chesnakas, C. J. & Simpson, R. L. 1994 Full three-dimensional measurements of the cross-flow separation region of a prolate spheroid. Exp. Fluids 17, 68–74.CrossRefGoogle Scholar
6. Chesnakas, C. J. & Simpson, R. L. 1996 Measurements of the turbulence structure in the vicinity of a three-dimensional separation. Trans. ASME: J. Fluids Engng 118, 268–275.Google Scholar
7. Chesnakas, C. J. & Simpson, R. L. 1997 Detailed investigation of the three-dimensional separation about a prolate spheroid. AIAA J. 35, 990–999.CrossRefGoogle Scholar
8. Constantinescu, G. S., Pasinato, H., Wang, Y.-Q., Forsythe, J. R. & Squires, K. D. 2002 Numerical investigation of flow past a prolate spheroid. Trans. ASME: J. Fluids Engng 124, 904–910.Google Scholar
9. El Khoury, G. K., Andersson, H. I. & Pettersen, B. 2010 Crossflow past a prolate spheroid at Reynolds number of 10 000. J. Fluid Mech. 659, 365–374.CrossRefGoogle Scholar
10. Fu, T. C., Shekarriz, A., Katz, J. & Huang, T. T. 1994 The flow structure in the lee of an inclined prolate spheroid. J. Fluid Mech. 269, 79–106.CrossRefGoogle Scholar
11. Goody, M. C., Simpson, R. L., Engel, M., Chesnakas, C. J. & Devenport, W. J. 1998 Mean velocity and pressure and velocity spectral measurements within a separated flow around a prolate spheroid at incidence. In 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA. AIAA Paper 98-0630–10. American Institute of Aeronautics and Astronautics.Google Scholar
12. Goody, M. C., Simpson, R. L. & Chesnakas, C. J. 2000 Separated flow surface pressure fluctuations and pressure–velocity correlations on prolate spheroid. AIAA J. 38, 266–274.CrossRefGoogle Scholar
13. Han, T. & Patel, V. C. 1979 Flow separation on a spheroid at incidence. J. Fluid Mech. 92, 643–657.CrossRefGoogle Scholar
14. Hussain, F. & Husain, H. S. 1989 Elliptic jets. Part 1. Characteristics of unexcited and exited jets. J. Fluid Mech. 208, 257–320.CrossRefGoogle Scholar
15. Hölzer, A. & Sommerfeld, M. 2009 Lattice Boltzmann simulations to determine drag, lift and torque acting on non-spherical particles. Comput. Fluids 38, 572–589.CrossRefGoogle Scholar
16. Inoue, O. & Sakuragi, A. 2008 Vortex shedding from a circular cylinder of finite length at low Reynolds numbers. Phys. Fluids 20, 033601.CrossRefGoogle Scholar
17. Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A. 102, 161–179.Google Scholar
18. Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
19. Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
20. Karlsson, A., Bensow, R. & Fureby, C. 2008 Numerical simulations of the flow around a prolate spheroid. In 11th Numerical Towing Tank Symposium, ENSIETA, Brest, France.Google Scholar
21. Kim, S. & Arunachalam, P. V. 1987 The general solution for an ellipsoid in low-Reynolds-number flow. J. Fluid Mech. 178, 535–547.CrossRefGoogle Scholar
22. Kim, S.-E., Rhee, S. H. & Cokljat, D. 2002 High-incidence and dynamic pitch-up maneuvering characteristics of a prolate spheroid - CFD Validation. In 24th Symposium on Naval Hydrodynamics, Fukuoka, Japan. National Academic Press.Google Scholar
23. Kim, S.-E., Rhee, S. H. & Cokljat, D. 2003 Application of modern turbulence models to vortical flow around a prolate spheroid at incidence. In 41st AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, USA. AIAA Paper 2003-0429–11.Google Scholar
24. Kiya, M. & Abe, Y. 1999 Turbulent elliptic wakes. J. Fluids Struct. 13, 1041–1067.CrossRefGoogle Scholar
25. Krothapalli, A., Baganoff, D. & Karamcheti, K. 1981 On the mixing of rectangular jets. J. Fluid Mech. 107, 201–220.CrossRefGoogle Scholar
26. Kuo, Y. H. & Baldwin, L. V. 1967 The formation of elliptical wakes. J. Fluid Mech. 27, 353–360.CrossRefGoogle Scholar
27. Lundell, F. & Carlsson, A. 2010 Heavy ellipsoids in creeping shear flow: transitions of the particle rotation rate and orbit shape. Phys. Rev. E 81, 016323–08.CrossRefGoogle ScholarPubMed
28. Manhart, M. 2004 A zonal algorithm for DNS of turbulent boundary layers. Comput. Fluids 33, 435–461.CrossRefGoogle Scholar
29. Meier, H. U. & Kreplin, H.-P. 1980 Experimental investigation of the boundary layer transition and separation on a body of revolution. Z. Flugwiss. Weltraumforsch. 4, 65–71.Google Scholar
30. Mortensen, P. H., Andersson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2008 Dynamics of prolate ellipsoidal particles in a turbulent channel flow. Phys. Fluids 20, 093302.CrossRefGoogle Scholar
31. Narasimhamurthy, V. D. & Andersson, H. I. 2009 Numerical simulation of the turbulent wake behind a normal flat plate. Intl J. Heat Fluid Flow 30, 1037–1043.CrossRefGoogle Scholar
32. Narasimhamurthy, V. D., Andersson, H. I. & Pettersen, B. 2009a Cellular vortex shedding behind a tapered circular cylinder. Phys. Fluids 21, 044106.CrossRefGoogle Scholar
33. Narasimhamurthy, V. D., Andersson, H. I. & Pettersen, B. 2009b Steady viscous flow past a tapered cylinder. Acta Mechanica 206, 53–57.CrossRefGoogle Scholar
34. Peller, N., Le Duc, A., Tremblay, F. & Manhart, M. 2006 High-order stable interpolations for immersed boundary methods. Intl J. Numer. Meth. Fluids 52, 1175–1193.CrossRefGoogle Scholar
35. Provansal, M., Schouveiler, L. & Leweke, T. 2004 From the double vortex street behind a cylinder to the wake of a sphere. Eur. J. Mech. B/Fluids 23, 65–80.CrossRefGoogle Scholar
36. Rhee, S. H. & Hino, T. 2000 Computational investigation of 3D turbulent flow separation around a spheroid using an unstructured grid method. J. Soc. Nav. Archit. Japan 188, 1–9.CrossRefGoogle Scholar
37. Saha, A. K. 2004 Three-dimensional numerical simulations of the transition of flow past a cube. Phys. Fluids 16, 1630–1646.CrossRefGoogle Scholar
38. Sakamoto, H. & Haniu, H. 1990 A study on vortex shedding from spheres in a uniform flow. Trans. ASME: J. Fluids Engng 112, 386–392.Google Scholar
39. Schouveiler, L. & Provansal, M. 2001 Periodic wakes of low aspect ratio cylinders with free hemispherical ends. J. Fluids Struct. 15, 565–573.CrossRefGoogle Scholar
40. Sforza, P. M., Steiger, M. H. & Trentacoste, N. 1966 Studies on three-dimensional viscous jets. AIAA J. 4, 800–806.CrossRefGoogle Scholar
41. Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004 Flow past a cylinder with free hemispherical ends: comments on grid independence and wake symmetry characteristics. In Proceedings of the 15th Australian Fluid Mechanics Conference. University of Sydney, Australia.CrossRefGoogle Scholar
42. Sheard, G. J., Thompson, M. C. & Hourigan, K. 2008 Flow normal to a short cylinder with hemispherical ends. Phys. Fluids 20, 041701.CrossRefGoogle Scholar
43. Shenoy, A. R. & Kleinstreuer, C. 2008 Flow over a thin circular disk at low to moderate Reynolds numbers. J. Fluid Mech. 605, 253–262.CrossRefGoogle Scholar
44. Stone, H. L. 1968 Iterative solution of implicit approximations of multidimensional partial differential equations. SIAM J. Numer. Anal. 5, 530–558.CrossRefGoogle Scholar
45. Sucker, D. & Brauer, H. 1975 Fluiddynamik bei quer angeströmten Zylindern. Wärme-Stoffübertrag 8, 149–158.CrossRefGoogle Scholar
46. Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.CrossRefGoogle Scholar
47. Wetzel, T. G. & Simpson, R. L. 1996 Unsteady three-dimensional cross-flow separation measurements on a prolate spheroid undergoing time-dependent maneuvers. In 21st Symposium on Naval Hydrodynamics. Trondheim, Norway. National Academic Press.Google Scholar
48. Wetzel, T. G. & Simpson, R. L. 1998 Unsteady crossflow separation location measurements on a maneuvering prolate spheroid. AIAA J. 36, 2063–2071.CrossRefGoogle Scholar
49. Wetzel, T. G., Simpson, R. L. & Chesnakas, C. J. 1998 Measurement of three-dimensional crossflow separation. AIAA J. 36, 557–564.CrossRefGoogle Scholar
50. Wikström, N., Svennberg, U., Alin, N. & Fureby, C. 2004 Large eddy simulation of the flow around an inclined prolate spheroid. J. Turbul. 5, 29.Google Scholar
51. Williamson, C. H. K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
52. Zaman, K. B. M. Q. 1996 Axis switching and spreading of an asymmetric jet: the role of coherent structure dynamics. J. Fluid Mech. 316, 1–27.CrossRefGoogle Scholar
53. Zamyshlyaev, A. A. & Shrager, G. R. 2004 Fluid flow past spheroids at moderate Reynolds numbers. Fluid Dyn. 39, 376–383.CrossRefGoogle Scholar
54. Zastawny, M., Mallouppas, G., Zhao, F. & Van Wachem, B. 2012 Derivation of drag and lift force and torque coefficients for non-spherical particles in flows. Intl J. Multiphase Flow 39, 227–239.CrossRefGoogle Scholar
55. Zdravkovich, M. M., Brand, V. P., Mathew, G. & Weston, A. 1989 Flow past short circular cylinders with two free ends. J. Fluid Mech. 203, 557–575.CrossRefGoogle Scholar
56. Zdravkovich, M. M. 1997 Flow Around Circular Cylinders. Oxford University Press.CrossRefGoogle Scholar