Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T19:21:00.091Z Has data issue: false hasContentIssue false
  • English
  • Français

Wake states and frequency selection of a streamwise oscillating cylinder

Published online by Cambridge University Press:  30 July 2013

Justin S. Leontini ,
David Lo Jacono  and
Mark C. Thompson
Justin S. Leontini*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
David Lo Jacono
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia Institut de Mécanique des Fluides de Toulouse (IMFT), CNRS, UPS, Université de Toulouse, Allée Camille Soula, F-31400 Toulouse, France
Mark C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents the results of an in-depth study of the flow past a streamwise oscillating cylinder, examining the impact of varying the amplitude and frequency of the oscillation, and the Reynolds number of the incoming flow. These findings are presented in a framework that shows that the relationship between the frequency of vortex shedding 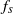${f}_{s} $ and the amplitude of oscillation 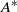${A}^{\ast } $ is governed by two primary factors: the first is a reduction of 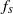${f}_{s} $ proportional to a series in 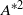${A}^{\ast 2} $ over a wide range of driving frequencies and Reynolds numbers; the second is nonlinear synchronization when this adjusted 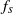${f}_{s} $ is in the vicinity of 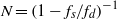$N= {(1- {f}_{s} / {f}_{d} )}^{- 1} $, where 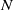$N$ is an integer. Typically, the influence of higher-order terms is small, and truncation to the first term of the series (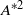${A}^{\ast 2} $) well represents the overall trend of vortex shedding frequency as a function of amplitude. However, discontinuous steps are overlaid on this trend due to the nonlinear synchronization. When 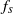${f}_{s} $ is normalized by the Strouhal frequency 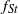${f}_{St} $ (the frequency of vortex shedding from an unperturbed cylinder), the rate at which 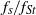${f}_{s} / {f}_{St} $ decreases with amplitude, at least for 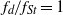${f}_{d} / {f}_{St} = 1$, shows a linear dependence on the Reynolds number. For a fixed 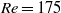$\mathit{Re}= 175$, the truncated series shows that the rate of decrease of 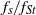${f}_{s} / {f}_{St} $ with amplitude varies as 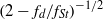${(2- {f}_{d} / {f}_{St} )}^{- 1/ 2} $ for 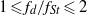$1\leqslant {f}_{d} / {f}_{St} \leqslant 2$, but is essentially independent of 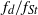${f}_{d} / {f}_{St} $ for 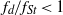${f}_{d} / {f}_{St} \lt 1$. These trends of the rate of decrease of 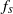${f}_{s} $ with respect to amplitude are also used to predict the amplitudes of oscillation around which synchronization occurs. These predicted amplitudes are shown to fall in regions of the parameter space where synchronized modes occur. Further, for the case of varying 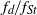${f}_{d} / {f}_{St} $, a very reasonable prediction of the amplitude of oscillation required for the onset of synchronization to the mode where 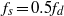${f}_{s} = 0. 5{f}_{d} $ is given. In a similar manner, amplitudes at which 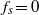${f}_{s} = 0$ are calculated, predicting where the natural vortex shedding is completely supplanted by the forcing. These amplitudes are found to coincide approximately with those at which the onset of a symmetric vortex shedding mode is observed. This result is interpreted as meaning that the symmetric shedding mode occurs when the dynamics crosses over from being dominated by the vortex shedding to being dominated by the forcing.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Vortex streets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 162 - 192
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al-Mdallal, Q. M., Lawrence, K. P. & Kocabiyik, S. 2007 Forced streamwise oscillations of a circular cylinder: locked-on modes and resulting fluid forces. J. Fluids Struct. 23 (5), 681–701.Google Scholar
Armstrong, B. J., Barnes, F. H. & Grant, I. 1986 The effect of a perturbation on the flow over a bluff cylinder. Phys. Fluids 29, 2095–2102.Google Scholar
Arnol’d, V. I. 1965 Small denominators. I Mappings of the circumference onto itself. Am. Math. Soc. Transl., Ser. 2 46, 215–284 (translated from 1961 Izv. Akad. Nauk SSSR Ser. Mat. 25, 1).Google Scholar
Barbi, C., Favier, D. P., Maresca, C. A. & Telionis, D. P. 1986 Vortex shedding and lock-on of a circular cylinder in oscillatory flow. J. Fluid Mech. 170, 527–544.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Cetiner, O. & Rockwell, D. 2001 Streamwise oscillations of a cylinder in a steady current. Part 1. Locked-on states of vortex formation and loading. J. Fluid Mech. 427, 1–28.Google Scholar
Gresho, P. M. & Sani, R. L. 1987 On pressure boundary conditions for the incompressible Navier–Stokes equations. Intl. J. Numer. Meth. Fluids 7, 1111–1145.Google Scholar
Griffin, O. M. & Ramberg, S. E. 1976 Vortex shedding from a cylinder vibrating in line with an incident uniform flow. J. Fluid Mech. 75 (2), 257–271.Google Scholar
Hall, M. S. & Griffin, O. M. 1993 Vortex shedding and lock-on in a perturbed flow. Trans. ASME: J. Fluids Engng 115, 283–291.Google Scholar
Jarża, A. & Podolski, M. 2004 Turbulence structure in the vortex formation region behind a circular cylinder in lock-on conditions. Eur. J. Mech. B/ 23 (3), 535–550.Google Scholar
Jauvtis, N. & Williamson, C. H. K. 2005 The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 509, 23–62.CrossRefGoogle Scholar
Jeon, D. & Gharib, M. 2004 On the relationship between the vortex formation process and cylinder wake vortex patterns. J. Fluid Mech. 519, 161–181.Google Scholar
Karniadakis, G. E. & Sherwin, S. J. 2005 Spectral/hp Element Methods for Computational Fluid Dynamics. Oxford University Press.Google Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1989 Frequency selection and asymptotic states in laminar wakes. J. Fluid Mech. 199, 441–469.Google Scholar
Kim, B. H. & Williams, D. R. 2006 Nonlinear coupling of fluctuating drag and lift on cylinders undergoing forced oscillations. J. Fluid Mech. 559, 335–353.Google Scholar
Konstantinidis, E. & Balabani, S. 2007 Symmetric vortex shedding in the near wake of a circular cylinder due to streamwise perturbations. J. Fluids Struct. 23, 1047–1063.Google Scholar
Konstantinidis, E., Balabani, S. & Yianneskis, M. 2003 The effect of flow perturbations on the near wake characteristics of a circular cylinder. J. Fluids Struct. 18, 367–386.Google Scholar
Konstantinidis, E., Balabani, S. & Yianneskis, M. 2005 The timing of vortex shedding in a cylinder wake imposed by periodic inflow perturbations. J. Fluid Mech. 543, 45–55.CrossRefGoogle Scholar
Konstantinidis, E., Balabani, S. & Yianneskis, M. 2007 Bimodal vortex shedding in a perturbed cylinder wake. Phys. Fluids 19, 011701.Google Scholar
Konstantinidis, E. & Bouris, D. 2009 Effect of nonharmonic forcing on bluff-body vortex dynamics. Phys. Rev. E 79, 045303(R).Google Scholar
Konstantinidis, E. & Bouris, D. 2010 The effect of nonharmonic forcing on bluff-body aerodynamics at a low Reynolds number. J. Wind Engng Ind. Aerodyn. 98 (6–7), 245–252.CrossRefGoogle Scholar
Konstantinidis, E. & Liang, C. 2011 Dynamic response of a turbulent cylinder wake to sinusoidal inflow perturbations across the vortex lock-on range. Phys. Fluids 23, 075102.Google Scholar
Le Gal, P., Nadim, A. & Thompson, M. C. 2001 Hysteresis in the forced Stuart–Landau equation: application to vortex shedding from an oscillating cylinder. J. Fluids Struct. 15, 445–457.Google Scholar
Leontini, J. S., Lo Jacono, D. & Thompson, M. C. 2011 A numerical study of an inline oscillating cylinder in a free stream. J. Fluid Mech. 688, 551–568.Google Scholar
Leontini, J. S., Stewart, B. E., Thompson, M. C. & Hourigan, K. 2006 Wake state and energy transitions of an oscillating cylinder at low Reynolds number. Phys. Fluids 18 (6), 067101.CrossRefGoogle Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2007 Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 577, 79–104.Google Scholar
Lo Jacono, D., Leontini, J. S., Thompson, M. C. & Sheridan, J. 2010 Modification of three-dimensional transition in the wake of a rotationally oscillating cylinder. J. Fluid Mech. 643, 349–362.CrossRefGoogle Scholar
Marzouk, O. A. & Nayfeh, A. H. 2009 Reduction of the loads on a cylinder undergoing harmonic in-line motion. Phys. Fluids 21, 083103.Google Scholar
Meneghini, J. R. & Bearman, P. W. 1995 Numerical simulation of high amplitude oscillatory flow about a circular cylinder. J. Fluids Struct. 9, 435–455.Google Scholar
Mureithi, N. W., Huynh, K., Rodriguez, M. & Pham, A. 2010 A simple low order model of the forced Kármán wake. Intl J. Mech. Sci. 52, 1522–1534.Google Scholar
Mureithi, N. W. & Rodriguez, M. 2005 Stability and bifurcation of a forced cylinder wake. In Proceedings of 2005 ASME International Mechanical Engineering Congress and Exposition, Orlando, FL.Google Scholar
Nazarinia, M., Lo Jacono, D., Thompson, M. C. & Sheridan, J. 2009 Flow behind a cylinder forced by a combination of oscillatory translational and rotational motions. Phys. Fluids 21 (5), 051701.Google Scholar
Nishihara, T., Kaneko, S. & Watanabe, T. 2005 Characteristics of fluid dynamic forces acting on a circular cylinder oscillated in the streamwise direction and its wake patterns. J. Fluids Struct. 20, 505–518.Google Scholar
Ongoren, A. & Rockwell, D. 1988 Flow structure from an oscillating cylinder. Part 2. Mode competition in the near wake. J. Wind Engng Ind. Aerodyn. 191, 225–245.Google Scholar
Perdikaris, P. G., Kaitsis, L. & Triantafyllou, G. S. 2009 Chaos in a cylinder wake due to forcing at the Strouhal frequency. Phys. Fluids 21, 101705.Google Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard–von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.Google Scholar
Rodriguez, M. & Mureithi, N. W. 2006 Cylinder wake dynamics in the presence of stream-wise harmonic forcing. In Proceedings of PVP2006-ICPVT-11 2006 ASME Pressure Vessels and Piping Division Conference, Vancouver, BC, Canada.Google Scholar
Tanida, Y., Okajima, A. & Watanabe, Y. 1973 Stability of a circular cylinder oscillating in uniform flow or in a wake. J. Fluid Mech. 61 (4), 769–784.Google Scholar
Tatsuno, M. 1972 Vortex streets behind a circular cylinder oscillating in the direction of flow. Bull. Res. Inst. Appl. Mech. Kyushu Univ. 36, 25–37.Google Scholar
Thompson, M. C., Hourigan, K., Cheung, A. & Leweke, T. 2006 Hydrodynamics of a particle impact on a wall. Appl. Math. Model. 30, 1356–1369.Google Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.Google Scholar
Tudball-Smith, D., Leontini, J. S., Lo Jacono, D. & Sheridan, J. 2012 Streamwise forced oscillations of circular and square cylinders. Phys. Fluids 24, 111703.Google Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31 (11), 3165–3168.Google Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.Google Scholar
Xu, S. J., Zhou, Y. & Wang, M. H. 2006 A symmetric binary-vortex street behind a longitudinally oscillating cylinder. J. Fluid Mech. 556, 27–43.Google Scholar
Yokoi, Y. & Kamemoto, K. 1994 Vortex shedding from an oscillating circular cylinder in a uniform flow. Exp. Therm. Fluid Sci. 8, 121–127.Google Scholar