Article contents
Wake behind a three-dimensional dry transom stern. Part 1. Flow structure and large-scale air entrainment
Published online by Cambridge University Press: 26 July 2019
Abstract
We present high-resolution implicit large eddy simulation (iLES) of the turbulent air-entraining flow in the wake of three-dimensional rectangular dry transom sterns with varying speeds and half-beam-to-draft ratios 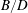 $B/D$. We employ two-phase (air/water), time-dependent simulations utilizing conservative volume-of-fluid (cVOF) and boundary data immersion (BDIM) methods to obtain the flow structure and large-scale air entrainment in the wake. We confirm that the convergent-corner-wave region that forms immediately aft of the stern wake is ballistic, thus predictable only by the speed and (rectangular) geometry of the ship. We show that the flow structure in the air–water mixed region contains a shear layer with a streamwise jet and secondary vortex structures due to the presence of the quasi-steady, three-dimensional breaking waves. We apply a Lagrangian cavity identification technique to quantify the air entrainment in the wake and show that the strongest entrainment is where wave breaking occurs. We identify an inverse dependence of the maximum average void fraction and total volume entrained with
$B/D$. We employ two-phase (air/water), time-dependent simulations utilizing conservative volume-of-fluid (cVOF) and boundary data immersion (BDIM) methods to obtain the flow structure and large-scale air entrainment in the wake. We confirm that the convergent-corner-wave region that forms immediately aft of the stern wake is ballistic, thus predictable only by the speed and (rectangular) geometry of the ship. We show that the flow structure in the air–water mixed region contains a shear layer with a streamwise jet and secondary vortex structures due to the presence of the quasi-steady, three-dimensional breaking waves. We apply a Lagrangian cavity identification technique to quantify the air entrainment in the wake and show that the strongest entrainment is where wave breaking occurs. We identify an inverse dependence of the maximum average void fraction and total volume entrained with 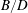 $B/D$. We determine that the average surface entrainment rate initially peaks at a location that scales with draft Froude number and that the normalized average air cavity density spectrum has a consistent value providing there is active air entrainment. A small parametric study of the rectangular geometry and stern speed establishes and confirms the scaling of the interface characteristics with draft Froude number and geometry. In Part 2 (Hendrikson & Yue, J. Fluid Mech., vol. 875, 2019, pp. 884–913) we examine the incompressible highly variable density turbulence characteristics and turbulence closure modelling.
$B/D$. We determine that the average surface entrainment rate initially peaks at a location that scales with draft Froude number and that the normalized average air cavity density spectrum has a consistent value providing there is active air entrainment. A small parametric study of the rectangular geometry and stern speed establishes and confirms the scaling of the interface characteristics with draft Froude number and geometry. In Part 2 (Hendrikson & Yue, J. Fluid Mech., vol. 875, 2019, pp. 884–913) we examine the incompressible highly variable density turbulence characteristics and turbulence closure modelling.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
Footnotes
Present address: Southampton Marine and Maritime Institute, University of Southampton, SO16 7QF, UK.
References
Hendrickson Supplementary Movie 1
Instantaneous isosurface of volume fraction f=0.5 for B/D=1, Fr=2.53 within the interrogation domain. Flow is from left to right (+x). Viewed from above.
Hendrickson Supplementary Movie 2
Instantaneous isosurface of volume fraction f=0.5 for B/D=1, Fr=2.53 within the interrogation domain. Flow is from left to right (+x). Viewed from side.
Hendrickson Supplementary Movie 3
Instantaneous isosurface of volume fraction f=0.5 for B/D=1.25, Fr=2.53 within the interrogation domain. Flow is from left to right (+x). Viewed from above.
Hendrickson Supplementary Movie 4
Instantaneous isosurface of volume fraction f=0.5 for B/D=1.25, Fr=2.53 within the interrogation domain. Flow is from left to right (+x). Viewed from side.
- 30
- Cited by


