Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T17:42:56.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Vorticity forces on an impulsively startedfinite plate

Published online by Cambridge University Press:  25 January 2012

Jian-Jhih Lee ,
Cheng-Ta Hsieh ,
Chien C. Chang  and
Chin-Chou Chu
Jian-Jhih Lee
Affiliation:
Institute of Applied Mechanics and Taida Institute of Mathematical Sciences, National Taiwan University, Taipei 106, Taiwan, ROC
Cheng-Ta Hsieh
Affiliation:
Institute of Applied Mechanics and Taida Institute of Mathematical Sciences, National Taiwan University, Taipei 106, Taiwan, ROC
Chien C. Chang*
Affiliation:
Institute of Applied Mechanics and Taida Institute of Mathematical Sciences, National Taiwan University, Taipei 106, Taiwan, ROC Division of Mechanics, Research Center for Applied Sciences, Academia Sinica, Taipei 115, Taiwan, ROC
Chin-Chou Chu*
Affiliation:
Institute of Applied Mechanics and Taida Institute of Mathematical Sciences, National Taiwan University, Taipei 106, Taiwan, ROC
*
†Email addresses for correspondence:[email protected], [email protected]
†Email addresses for correspondence:[email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study, we consider various contributions to the forces on an impulsively started finite plate from the perspective of a diagnostic vorticity force theory. The wing plate has an aspect ratio (AR) between 1 and 3, and is placed at low and high angles of attack (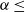 and 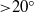), while the Reynolds number is either 100 or 300. The theory enables us to quantify the contributions to the forces exerted on the plate in terms of all of the fluid elements with non-zero vorticity, such as in the tip vortices (TiVs), leading- and trailing-edge vortices (LEV and TEV) as well on the plate surface. This line of force analysis has been pursued for two-dimensional flow in our previous studies. In contrast to the pressure force analysis (PFA), the vorticity force analysis (VFA) reveals new salient features in its applications to three-dimensional flow by examining sectional force contributions along the spanwise direction. In particular, at a large aspect ratio (), the force distributions of PFA and VFA show close agreements with each other in the middle sections, while at a lower aspect ratio (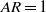), the force distribution of PFA is substantially larger than that of VFA in most of the sections. The difference is compensated for by the contributions partly by the edge sections and mainly by the vortices in the outer regions. Further investigation is made fruitful by decomposing the vorticity into the spanwise (longitudinal) component (the only one in two-dimensional flow) and the other two orthogonal (transverse) components. The relative importance of the force contributions credited to the transverse components in the entire flow regions as well as in the two outer regions signifies the three-dimensional nature of the flow over a finite plate. The interplay between the LEV and the TiVs at various time stages is shown to play a key role in distinguishing the force contributions for the plate with a smaller aspect ratio and that with a larger aspect ratio. The present VFA provides a better perspective for flow control by relating the forces directly to the various sources of vorticity (or vortex structures) on or near the wing plate.

JFM classification

Aerodynamics: Aerodynamics Biological Fluid Dynamics: Swimming/flying
Type
Papers
Information
Journal of Fluid Mechanics , Volume 694 , 10 March 2012 , pp. 464 - 492
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bartlett, G. E. & Vidal, R. J. R. 1955 Experimental investigation of influence of edge shape on the aerodynamic characteristics of low aspect ratio wings at low speeds. J. Aero. Sci. 22, 517–533.CrossRefGoogle Scholar
2. Biesheuvel, A. & Hagmeijer, R. 2006 On the force on a body moving in fluid. Fluid Dyn. Res. 38, 716–742.CrossRefGoogle Scholar
3. Birch, J. M., Dickson, W. B. & Dickinson, M. H. 2004 Force production and flow structure of the leading edge vortex on flapping wings at high and low Reynolds numbers. J. Expl. Biol. 207, 1063–1072.CrossRefGoogle Scholar
4. Bollay, W. 1939 A nonlinear wing theory and its application to rectangular wings of small aspect ratio. Z. Angew. Math. Mech. 19, 21–35.CrossRefGoogle Scholar
5. Burgers, J. M. 1920 On the resistance of fluids and vortex motion. Proc. Kon. Akad. Westenschappente Amsterdam 1, 774–782.Google Scholar
6. Chang, C. C. 1992 Potential flow and forces for incompressible viscous flow. Proc. R. Soc. A-Math. Phys. Eng. Sci. 437, 517–525.Google Scholar
7. Chang, C. C., Yang, S. H. & Chu, C. C. 2008 A many-body force decomposition with applications to flow about bluff bodies. J. Fluid Mech. 600, 95–104.CrossRefGoogle Scholar
8. Cosyn, P. & Vierendeels, J. 2006 Numerical investigation of low-aspect-ratio wings at low Reynolds numbers. J. Aircraft 43, 713–722.CrossRefGoogle Scholar
9. Ellington, C. P., Van Den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384, 626–630.CrossRefGoogle Scholar
10. Freymuth, P., Bank, W. & Finaish, F. 1987 Further visualization of combined wing tip and starting vortex systems. AIAA J. 25, 1153–1159.CrossRefGoogle Scholar
11. Howarth, L. 1935 The theoretical determination of the lift coefficient for a thin elliptic cylinder. Proc. R. Soc. Lond. Ser. A 149, 558–586.Google Scholar
12. Howe, M. S. 1995 On the force and moment on a body in an incompressible fluid, with application to rigid bodies and bubbles at high and low Reynolds numbers. Quart. J. Mech. Appl. Math. 48, 401–426.CrossRefGoogle Scholar
13. Howe, M. S., Lauchle, G. C. & Wang, J. 2001 Aerodynamic lift and drag fluctuations of a sphere. J. Fluid Mech. 436, 41–57.CrossRefGoogle Scholar
14. Hsieh, C. T., Chang, C. C. & Chu, C. C. 2009 Revisiting the aerodynamics of hovering flight using simple models. J. Fluid Mech. 623, 121–148.CrossRefGoogle Scholar
15. Hsieh, C. T., Kung, C. F., Chang, C. C. & Chu, C. C. 2010 Unsteady aerodynamics of dragonfly using a simple wing-wing model from the perspective of a force decomposition. J. Fluid Mech. 663, 233–252.CrossRefGoogle Scholar
16. Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, stream, and convergence zones in turbulent flows, Center for Turbulence Research Report CTR-S88, pp. 193–208.Google Scholar
17. Kambe, T. 1986 Acoustic emissions by vortex motions. J. Fluid Mech. 173, 643–666.CrossRefGoogle Scholar
18. Kim, D & Gharib, M. 2010 Experimental study of three-dimensional vortex structures in translating and rotating plates. Exp. Fluids. 49, 329–339.CrossRefGoogle Scholar
19. Lamar, J. E. 1974 Extension of leading-edge-suction analogy to wings with separated flow around the side edges at subsonic speeds. NASA TR R-428, L-9460.Google Scholar
20. Lamar, J. E. 1976 Prediction of vortex flow characteristics of wings at subsonic and supersonic speeds. J. Aircraft 13, 490–494.CrossRefGoogle Scholar
21. Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Pergamon.Google Scholar
22. Lighthill, M. J. 1979 Wave and hydrodynamic loading. Proc. Second Intl Conf. Behaviour Off-Shore Struct., BHRA Cranfield 1, 1–40.Google Scholar
23. Lighthill, M. J. 1986 Fundamentals concerning wave loading on offshore structures. J. Fluid Mech. 173, 667–681.CrossRefGoogle Scholar
24. Magnaudet, J. 2011 A ‘reciprocal’ theorem for the prediction of loads on a body moving in an inhomogeneous flow at arbitrary Reynolds number. J. Fluid Mech. 689, 564–604.CrossRefGoogle Scholar
25. Maxworthy, T. 1979 Experiments on the Weis-Fogh mechanism of lift generation by insects in hovering flight. Part I. Dynamics of the fling. J. Fluid Mech. 93, 47–63.CrossRefGoogle Scholar
26. Payne, R. B. 1958 Calculations of unsteady flow past a circular cylinder. J. Fluid Mech. 3, 81–86.CrossRefGoogle Scholar
27. Phillips, O. M. 1956 The intensity of aeolian tones. J. Fluid Mech. 1, 607–624.CrossRefGoogle Scholar
28. Polhamus, E. C. 1971 Predictions of vortex-lift characteristics by a Leading–Edge–Suction analogy. J. Aircraft 8, 193–199.CrossRefGoogle Scholar
29. Quartapelle, L. & Napolitano, M. 1983 Force and moment in incompressible flows. AIAA J. 22, 1713–1718.Google Scholar
30. Ringuette, M. J., Milano, M. & Gharib, M. 2007 Role of the tip vortex in the force generation of low-aspect-ratio normal flat plates. J. Fluid Mech. 581, 453–468.CrossRefGoogle Scholar
31. Sears, W. R. 1956 Some recent developments in airfoil theory. J. Aeronaut. Sci. 23, 490–499.CrossRefGoogle Scholar
32. Sears, W. R. 1976 Unsteady motion of airfoil with boundary layer separation. AIAA J. 14, 216–220.CrossRefGoogle Scholar
33. Shyy, W., Aono, H., Chimakurthi, S. K., Trizila, P., Kang, C. K., Cesnik, C. E. S. & Liu, H. 2010 Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aeronaut. Sci. 46, 254–327.CrossRefGoogle Scholar
34. Taira, K. & Colonius, T. 2009 Three-dimensional separated flows around low-aspect-ratio flat plates. J. Fluid Mech. 623, 187–207.CrossRefGoogle Scholar
35. Torres, G. E. & Mueller, T. J. 2004 Low-aspect-ratio wing aerodynamics at low Reynolds numbers. AIAA J. 42 (5), 865–873.CrossRefGoogle Scholar
36. Wells, J. C. 1996 A geometrical interpretation of force on a translating body in rotational flow. Phys. Fluids 8, 442–450.CrossRefGoogle Scholar
37. Winter, H. 1936 Flow phenomena on plates and aerofoils of short span. Tech. Rep. TM 798, NACA.Google Scholar
38. Wu, J. C. 1981 Theory for aerodynamic force and moment in viscous flows. AIAA J. 19, 432–441.CrossRefGoogle Scholar