Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-30T21:43:03.192Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex-induced vibrations: a soft coral feeding strategy?

Published online by Cambridge University Press:  14 April 2021

Mouad Boudina Open the ORCID record for Mouad Boudina [Opens in a new window] ,
Frédérick P. Gosselin Open the ORCID record for Frédérick P. Gosselin [Opens in a new window]  and
Stéphane Étienne
Mouad Boudina*
Affiliation:
Department of Mechanical Engineering, Polytechnique Montréal, Montréal, H3T 1J4Québec, Canada Laboratory for Multiscale Mechanics (LM2), Polytechnique Montréal, Montréal, H3T 1J4Québec, Canada
Frédérick P. Gosselin
Affiliation:
Department of Mechanical Engineering, Polytechnique Montréal, Montréal, H3T 1J4Québec, Canada Laboratory for Multiscale Mechanics (LM2), Polytechnique Montréal, Montréal, H3T 1J4Québec, Canada
Stéphane Étienne
Affiliation:
Department of Mechanical Engineering, Polytechnique Montréal, Montréal, H3T 1J4Québec, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

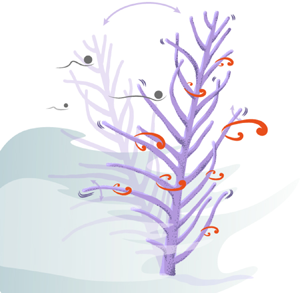
Soft corals, such as the bipinnate sea plume Antillogorgia bipinnata, are colony building animals that feed by catching food particles brought by currents. Because of their flexible skeleton, they bend and sway back and forth with the wave swell. In addition to this low-frequency sway of the whole colony, branches of A. bipinnata vibrate at high frequency with small amplitude and transverse to the flow as the wave flow speed peaks. In this paper, we investigate the origin of these yet unexplained vibrations and consider their effect on soft corals. Estimation of dynamical variables along with finite element implementation of the wake-oscillator model favour vortex-induced vibrations (VIVs) as the most probable origin of the observed rapid dynamics. To assess the impact of the dynamics on filter feeding, we simulated particles advected by the flow around a circular cylinder and calculated the capture rate with an in-house monolithic fluid–structure interaction (FSI) finite element solver and Python code. We observe that vibrating cylinders can capture up to 40 % more particles than fixed cylinders at frequency lock-in. Therefore, VIVs plausibly offer soft corals a better food capture.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Vortex Flows: Vortex instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 916 , 10 June 2021 , A50
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alnæs, M., Blechta, J., Hake, J., Johansson, A., Kehlet, B., Logg, A., Richardson, C., Ring, J., Rognes, M.E. & Wells, G.N. 2015 The FEniCS project version 1.5. Arch. Numer. Softw. 3 (100), 9–23.Google Scholar
Barton, I.E. 1995 Computation of particle tracks over a backward-facing step. J. Aero. Sci. 26 (6), 887–901.CrossRefGoogle Scholar
Bayer, F.M. 1961 The Shallow-Water Octocorallia of the West Indian Region. Studies on the Fauna of Curaçao and other Caribbean Islands, vol. 12 (1), 1–373.Google Scholar
Béguin, C., Pelletier, É. & Étienne, S. 2016 Void fraction influence on added mass in a bubbly flow. Eur. J. Mech. B/Fluids 56, 28–45.CrossRefGoogle Scholar
Bishop, R.E.D. & Hassan, A.Y. 1964 The lift and drag forces on a circular cylinder oscillating in a flowing fluid. Proc. R. Soc. Lond. A 277 (1368), 51–75.Google Scholar
Blevins, R.D. 1990 Flow-Induced Vibration. Van Nostrand Reinhold.Google Scholar
Boudina, M., Gosselin, F.P. & Étienne, S. 2020 Direct interception or inertial impaction? A theoretical derivation of the efficiency power law for a simple and practical definition of capture modes. Phys. Fluids 32 (12), 123603.CrossRefGoogle Scholar
Brennen, C.E. 1982 A review of added mass and fluid inertial forces. Tech. Rep. CR 08-101. Naval Civil Engineering Laboratory.Google Scholar
Buckingham, E. 1914 On physically similar systems; illustrations of the use of dimensional equations. Phys. Rev. 4 (4), 345–376.CrossRefGoogle Scholar
Cairns, S.D. 1977 A checklist of the ahermatypic Scleractinia of the Gulf of Mexico, with the description of a new species. Gulf Caribbean Res. 6 (1), 9–15.Google Scholar
Chance, M.M. & Craig, D.A. 1986 Hydrodynamics and behaviour of Simuliidae larvae (Diptera). Can. J. Zool. 64 (6), 1295–1309.CrossRefGoogle Scholar
Chaplin, J.R., Bearman, P.W., Huera Huarte, F.J. & Pattenden, R.J. 2005 Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current. J. Fluids Struct. 21 (1), 3–24.CrossRefGoogle Scholar
Clift, R., Grace, J.R. & Weber, M.E. 1978 Bubbles, Drops, and Particles. Academic Press.Google Scholar
Cori, J.-F., Etienne, S., Garon, A. & Pelletier, D. 2015 High-order implicit Runge–Kutta time integrators for fluid-structure interactions. Intl J. Numer. Meth. Fluids 78 (7), 385–412.CrossRefGoogle Scholar
Der Loughian, C., Tadrist, L., Allain, J.-M., Diener, J., Moulia, B. & de Langre, E. 2014 Measuring local and global vibration modes in model plants. C. R. Mécanique 342 (1), 1–7.CrossRefGoogle Scholar
Espinosa-Gayosso, A., Ghisalberti, M., Ivey, G.N. & Jones, N.L. 2012 Particle capture and low-Reynolds-number flow around a circular cylinder. J. Fluid Mech. 710, 362–378.CrossRefGoogle Scholar
Espinosa-Gayosso, A., Ghisalberti, M., Ivey, G.N. & Jones, N.L. 2013 Particle capture by a circular cylinder in the vortex-shedding regime. J. Fluid Mech. 733, 171–188.CrossRefGoogle Scholar
Espinosa-Gayosso, A., Ghisalberti, M., Ivey, G.N. & Jones, N.L. 2015 Density-ratio effects on the capture of suspended particles in aquatic systems. J. Fluid Mech. 783, 191–210.CrossRefGoogle Scholar
Etienne, S., Garon, A. & Pelletier, D. 2009 Perspective on the geometric conservation law and finite element methods for ALE simulations of incompressible flow. J. Comput. Phys. 228 (7), 2313–2333.CrossRefGoogle Scholar
Etienne, S. & Pelletier, D. 2012 The low Reynolds number limit of vortex-induced vibrations. J. Fluids Struct. 31, 18–29.CrossRefGoogle Scholar
Evangelinos, C. & Karniadakis, G.E. 1999 Dynamics and flow structures in the turbulent wake of rigid and flexible cylinders subject to vortex-induced vibrations. J. Fluid Mech. 400, 91–124.CrossRefGoogle Scholar
Fabricius, K.E. 2011 Octocorallia. In Encyclopedia of Modern Coral Reefs (ed. D. Hopley), pp. 740–745. Springer Science and Business Media.CrossRefGoogle Scholar
Facchinetti, M.L., de Langre, E. & Biolley, F. 2004 a Coupling of structure and wake oscillators in vortex-induced vibrations. J. Fluids Struct. 19 (2), 123–140.CrossRefGoogle Scholar
Facchinetti, M.L., de Langre, E. & Biolley, F. 2004 b Vortex-induced travelling waves along a cable. Eur. J. Mech. B/Fluids 23 (1), 199–208.CrossRefGoogle Scholar
Fredsøe, J. & Sumer, M.B. 2006 Hydrodynamics Around Cylindrical Structures, Revised edn. World Scientific.Google Scholar
Gilpin, W., Prakash, V.N. & Prakash, M. 2017 Vortex arrays and ciliary tangles underlie the feeding–swimming trade-off in starfish larvae. Nat. Phys. 13 (4), 380–386.CrossRefGoogle Scholar
Gosselin, F.P. 2019 Mechanics of a plant in fluid flow. J. Expl Bot. 70 (14), 3533–3548.CrossRefGoogle Scholar
Haugen, N.E.L. & Kragset, S. 2010 Particle impaction on a cylinder in a crossflow as function of Stokes and Reynolds numbers. J. Fluid Mech. 661, 239–261.CrossRefGoogle Scholar
Hay, A., Etienne, S., Garon, A. & Pelletier, D. 2015 a Time-integration for ALE simulations of fluid–structure interaction problems: stepsize and order selection based on the BDF. Comput. Meth. Appl. Mech. Engng 295, 172–195.CrossRefGoogle Scholar
Hay, A., Etienne, S., Pelletier, D. & Garon, A. 2015 b hp-Adaptive time integration based on the BDF for viscous flows. J. Comput. Phys. 291, 151–176.CrossRefGoogle Scholar
Hay, A., Yu, K.R., Etienne, S., Garon, A. & Pelletier, D. 2014 High-order temporal accuracy for 3D finite-element ALE flow simulations. Comput. Fluids 100, 204–217.CrossRefGoogle Scholar
Huera-Huarte, F.J. & Gharib, M. 2011 Flow-induced vibrations of a side-by-side arrangement of two flexible circular cylinders. J. Fluids Struct. 27 (3), 354–366.CrossRefGoogle Scholar
Inoue, S., Kayanne, H., Yamamoto, S. & Kurihara, H. 2013 Spatial community shift from hard to soft corals in acidified water. Nat. Clim. Change 3 (7), 683–687.CrossRefGoogle Scholar
Jeyasuria, P. & Lewis, J.C. 1987 Mechanical properties of the axial skeleton in gorgonians. Coral Reefs 5 (4), 213–219.CrossRefGoogle Scholar
Khalak, A. & Williamson, C.H.K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7), 813–851.CrossRefGoogle Scholar
Kim, S., Park, H., Gruszewski, H.A., Schmale, D.G. & Jung, S. 2019 Vortex-induced dispersal of a plant pathogen by raindrop impact. Proc. Natl Acad. Sci. USA 116 (11), 4917–4922.CrossRefGoogle ScholarPubMed
Krick, J. & Ackerman, J.D. 2015 Adding ecology to particle capture models: numerical simulations of capture on a moving cylinder in crossflow. J. Theor. Biol. 368, 13–26.CrossRefGoogle ScholarPubMed
de Langre, E. 2008 Effects of wind on plants. Annu. Rev. Fluid Mech. 40 (1), 141–168.CrossRefGoogle Scholar
Leclercq, T. & de Langre, E. 2018 Reconfiguration of elastic blades in oscillatory flow. J. Fluid Mech. 838, 606–630.CrossRefGoogle Scholar
Lei, J. & Nepf, H. 2019 Blade dynamics in combined waves and current. J. Fluids Struct. 87, 137–149.CrossRefGoogle Scholar
Löhner, R. 2008 Applied Computational Fluid Dynamics Techniques: An Introduction Based on Finite Element Methods. John Wiley and Sons.CrossRefGoogle Scholar
Löhner, R. & Ambrosiano, J. 1990 A vectorized particle tracer for unstructured grids. J. Comput. Phys. 91 (1), 22–31.CrossRefGoogle Scholar
Lucor, D., Mukundan, H. & Triantafyllou, M.S. 2006 Riser modal identification in CFD and full-scale experiments. J. Fluids Struct. 22 (6), 905–917.CrossRefGoogle Scholar
Maxey, M.R. & Riley, J.J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.CrossRefGoogle Scholar
McCombe, D. & Ackerman, J.D. 2018 Collector motion affects particle capture in physical models and in wind pollination. Am. Nat. 192 (1), 81–93.CrossRefGoogle ScholarPubMed
Monismith, S.G. 2007 Hydrodynamics of coral reefs. Annu. Rev. Fluid Mech. 39 (1), 37–55.CrossRefGoogle Scholar
Nakamura, Y., Hirata, K. & Kashima, K. 1994 Galloping of a circular cylinder in the presence of a splitter plate. J. Fluids Struct. 8 (4), 355–365.CrossRefGoogle Scholar
NDBC 2020 https://www.ndbc.noaa.gov/.Google Scholar
Newman, D.J. & Karniadakis, G.E.M. 1997 A direct numerical simulation study of flow past a freely vibrating cable. J. Fluid Mech. 344, 95–136.CrossRefGoogle Scholar
Niklas, K.J. 2015 A biophysical perspective on the pollination biology of ephedra nevadensis and E. trifurca. Bot. Rev. 81 (1), 28–41.CrossRefGoogle Scholar
Nova South Eastern University 2016 South Florida Octocorals: A Guide to Identification.Google Scholar
Ounis, H. & Ahmadi, G. 1990 Analysis of dispersion of small spherical particles in a random velocity field. J. Fluids Engng 112 (1), 114–120.CrossRefGoogle Scholar
Païdoussis, M.P., Price, S.J. & de Langre, E. 2010 Fluid-Structure Interactions: Cross-Flow-Induced Instabilities. Cambridge University Press.CrossRefGoogle Scholar
Palmer, M.R., Nepf, H.M., Pettersson, T.J.R. & Ackerman, J.D. 2004 Observations of particle capture on a cylindrical collector: implications for particle accumulation and removal in aquatic systems. Limnol. Oceanogr. 49 (1), 76–85.CrossRefGoogle Scholar
Paradvect 2020 Paradvect (PARticle ADVECTion): a Python code to simulate the trajectory of particles advected by a fluid flow.Google Scholar
Persillon, H. & Braza, M. 1998 Physical analysis of the transition to turbulence in the wake of a circular cylinder by three-dimensional Navier–Stokes simulation. J. Fluid Mech. 365, 23–88.CrossRefGoogle Scholar
Ribes, M., Coma, R. & Gili, J.-M. 1998 Heterotrophic feeding by gorgonian corals with symbiotic zooxanthella. Limnol. Oceanogr. 43 (6), 1170–1179.CrossRefGoogle Scholar
RodiCS 2020 RodiCS: A Finite Element Solver of Kirchhoff Rods under Fluid Flow and More. Available at: https://zenodo.org/record/4023287.Google Scholar
Rodriguez, M., de Langre, E. & Moulia, B. 2008 A scaling law for the effects of architecture and allometry on tree vibration modes suggests a biological tuning to modal compartmentalization. Am. J. Bot. 95 (12), 1523–1537.CrossRefGoogle ScholarPubMed
Rodriguez, M., Ploquin, S., Moulia, B. & de Langre, E. 2012 The multimodal dynamics of a walnut tree: experiments and models. Trans. ASME J. Appl. Mech. 79 (4), 044505.CrossRefGoogle Scholar
Sánchez, J.A., Aguilar, C., Dorado, D. & Manrique, N. 2007 Phenotypic plasticity and morphological integration in a marine modular invertebrate. BMC Evol. Biol. 7 (1), 122.CrossRefGoogle Scholar
Sarpkaya, T. 2010 Wave Forces on Offshore Structures. Cambridge University Press.CrossRefGoogle Scholar
Schindelin, J., et al. 2012 Fiji: an open-source platform for biological-image analysis. Nat. Meth. 9 (7), 676–682.CrossRefGoogle ScholarPubMed
Shimeta, J. & Jumars, P.A. 1991 Physical mechanisms and rates of particle capture by suspension-feeders. Oceanogr. Mar. Biol. 29 (19), 191–257.Google Scholar
Shimeta, J. & Koehl, M.A.R. 1997 Mechanisms of particle selection by tentaculate suspension feeders during encounter, retention, and handling. J. Expl Mar. Biol. Ecol. 209 (1), 47–73.CrossRefGoogle Scholar
Taylor, C. & Hood, P. 1973 A numerical solution of the Navier–Stokes equations using the finite element technique. Comput. Fluids 1 (1), 73–100.CrossRefGoogle Scholar
Taylor, G.I. 1952 Analysis of the swimming of long and narrow animals. Proc. R. Soc. Lond. A 214 (1117), 158–183.Google Scholar
Tsounis, G. & Edmunds, P.J. 2017 Three decades of coral reef community dynamics in St. John, USVI: a contrast of scleractinians and octocorals. Ecosphere 8 (1), e01646.CrossRefGoogle Scholar
Veron, J.E.N. 2011 Corals: biology, skeletal deposition, and reef-building. In Encyclopedia of Modern Coral Reefs (ed. D. Hopley), pp. 275–281. Springer Science and Business Media.CrossRefGoogle Scholar
Violette, R., de Langre, E. & Szydlowski, J. 2007 Computation of vortex-induced vibrations of long structures using a wake oscillator model: comparison with DNS and experiments. Comput. Struct. 85 (11), 1134–1141.CrossRefGoogle Scholar
Vogel, S. 1984 Drag and flexibility in sessile organisms. Am. Zool. 24 (1), 37–44.CrossRefGoogle Scholar
Wainwright, S.A. & Dillon, J.R. 1969 On the orientation of sea fans (Genus Gorgonia). Biol. Bull. 136, 130–139.CrossRefGoogle Scholar
Weber, M.E. & Paddock, D. 1983 Interceptional and gravitational collision efficiencies for single collectors at intermediate Reynolds numbers. J. Colloid Interface Sci. 94 (2), 328–335.CrossRefGoogle Scholar
Widahl, L.-E. 1992 Flow patterns around suspension-feeding mosquito larvae (Diptera: Culicidae). Ann. Entomol. Soc. Am. 85 (1), 91–95.CrossRefGoogle Scholar
Williams, G.C. & Chen, J.-Y. 2012 Resurrection of the octocorallian genus Antillogorgia for Caribbean species previously assigned to Pseudopterogorgia, and a taxonomic assessment of the relationship of these genera with Leptogorgia (Cnidaria, Anthozoa, Gorgoniidae). Zootaxa 3505, 39–52.CrossRefGoogle Scholar
Williamson, C.H.K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36 (1), 413–455.CrossRefGoogle Scholar
YouTube 2013 Caribbean Spiny Lobster and a Bipinnate Sea Plume coral. Available at: https://youtu.be/1mgayfgyfyw.Google Scholar
Yu, K.R., Étienne, S., Hay, A. & Pelletier, D. 2015 Code verification for unsteady 3-D fluid–solid interaction problems. Theor. Comput. Fluid Dyn. 29 (5), 455–471.CrossRefGoogle Scholar
Yu, K.R., Étienne, S., Scolan, Y.-M., Hay, A., Fontaine, E. & Pelletier, D. 2016 Flow-induced vibrations of in-line cylinder arrangements at low Reynolds numbers. J. Fluids Struct. 60, 37–61.CrossRefGoogle Scholar
Supplementary material: File

Boudina et al. supplementary material

Boudina et al. supplementary material

Download Boudina et al. supplementary material(File)
File 1.1 MB