Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T22:53:56.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex-corner interactions in a cavity shear layer elucidated by time-resolved measurements of the pressure field

Published online by Cambridge University Press:  11 July 2013

Xiaofeng Liu  and
Joseph Katz
Xiaofeng Liu
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Joseph Katz*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow structure and turbulence in an open cavity shear layer has been investigated experimentally at a Reynolds number of 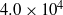$4. 0\times 1{0}^{4} $, with an emphasis on interactions of the unsteady pressure field with the cavity corners. A large database of time-resolved two-dimensional PIV measurements has been used to obtain the velocity distributions and calculate the pressure by spatially integrating the material acceleration at a series of sample areas covering the entire shear layer and the flow surrounding the corners. Conditional sampling, low-pass filtering and time correlations among variables enable us to elucidate several processes, which have distinctly different frequency ranges, that dominate the shear layer interactions with the corners. Kelvin–Helmholtz shear layer eddies have the expected Strouhal number range of 0.5–3.2. Their interactions with the trailing corner introduce two sources of vorticity fluctuations above the corner. The first is caused by the expected advection of remnants of the shear layer eddies. The second source involves fluctuations in local viscous vorticity flux away from the wall caused by periodic variations in the streamwise pressure gradients. This local production peaks when the shear layer vortices are located away from the corner, creating a lingering region with peak vorticity just above the corner. The associated periodic pressure minima there are lower than any other point in the entire flow field, making the region above the corner most prone to cavitation inception. Flapping of the shear layer and boundary layer upstream of the leading corner occurs at very low Strouhal numbers of ∼0.05, affecting all the flow and turbulence quantities around both corners. Time-dependent correlations of the shear layer elevation show that the flapping starts in the boundary layer upstream of the leading corner and propagates downstream at the free stream speed. Near the trailing corner, when the shear layer elevation is low, the stagnation pressure in front of the wall, the downward jetting flow along this wall, the fraction of shear layer vorticity entrained back into the cavity, and the magnitude of the pressure minimum above the corner are higher than those measured when the shear layer is high. However, the variations in downward jetting decay rapidly with increasing distance from the trailing corner, indicating that it does not play a direct role in a feedback mechanism that sustains the flapping. There is also low correlation between the boundary/shear layer elevation and the returning flow along the upstream vertical wall, providing little evidence that this returning flow affects the flapping directly. However, the characteristic period of flapping, ∼0.6 s, is consistent with recirculation time of the fluid within the cavity away from boundaries. The high negative correlations of shear/boundary layer elevation with the streamwise pressure gradient above the leading corner introduce a plausible mechanism that sustains the flapping: when the shear layer is low, the boundary layer is subjected to high adverse streamwise pressure gradients that force it to widen, and when the shear layer is high, the pressure gradients decrease, allowing the boundary layer to thin down. Flow mechanisms that would cause the flapping-induced pressure changes, and their relations to the flow within the cavity are discussed.

JFM classification

Turbulent Flows: Shear layer turbulence Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 728 , 10 August 2013 , pp. 417 - 457
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Christensen, K. T. & Liu, Z.-C. 2000 Analysis and interpretation of instantaneous turbulent velocity fields. Exp. Fluids 29, 275–290.Google Scholar
Andreopoulos, J. & Agui, J. H. 1996 Wall-vorticity flux dynamics in a two-dimensional turbulent boundary layer. J. Fluid Mech. 309, 45–84.CrossRefGoogle Scholar
Ashcroft, G. & Zhang, X. 2005 Vortical structures over rectangular cavities at low speed. Phys. Fluids 17, 015104.Google Scholar
Bendat, J. S. & Piersol, A. G. 2000 Random Data Analysis and Measurement Procedures. Wiley.Google Scholar
Blake, W. K. 1986 Mechanics of Flow-induced Sound and Vibration. Academic.Google Scholar
Bres, G. A. & Colonius, T. 2008 Three-dimensional instabilities in compressible flow over open cavities. J. Fluid Mech. 599, 309–339.Google Scholar
Chang, K., Constantinescu, G. & Park, S.-O. 2006 Analysis of the flow and mass transfer processes for the incompressible flow past an open cavity with a laminar and a fully turbulent incoming boundary layer. J. Fluid Mech. 561, 113–145.Google Scholar
Charonko, J. J., King, C. V., Smith, B. L. & Vlachos, P. P. 2010 Assessment of pressure field calculations from particle image velocimetry measurements. Meas. Sci. Tech. 21, 105401.Google Scholar
Gharib, M. 1987 Response of the cavity shear layer oscillations to external forcing. AIAA J. 25 (1), 43–47.CrossRefGoogle Scholar
Gharib, M. & Roshko, A. 1987 The effect of flow oscillations on cavity drag. J. Fluid Mech. 177, 501–530.Google Scholar
Gopalan, S. & Katz, J. 2000 Flow structure and modelling issues in the closure region of attached cavitation. Phys. Fluids 12, 895–911.CrossRefGoogle Scholar
Hackett, E. E., Luznik, L., Katz, J. & Osborn, T. R. 2009 Effect of finite spatial resolution on the turbulent energy spectrum measured in the coastal ocean bottom boundary layer. J. Atmos. Ocean. Technol. 26, 2610–2625.CrossRefGoogle Scholar
Haigermoser, C. 2009 Application of an acoustic analogy to PIV data from rectangular cavity flows. Exp. Fluids 47, 145–157.Google Scholar
Haigermoser, C., Vesely, L., Novara, M. & Onorato, M. 2008 A time-resolved particle image velocimetry investigation of a cavity flow with a thick incoming turbulent boundary layer. Phys. Fluids 20, 105101.CrossRefGoogle Scholar
Huang, X. Y. & Weaver, D. S. 1991 On the active control of shear layer oscillations across a cavity in the presence of pipeline acoustic resonance. J. Fluids Struct. 5, 207–219.Google Scholar
Kang, W., Lee, S. B. & Sung, H. J. 2008 Self-sustained oscillations of turbulent flows over an open cavity. Exp. Fluids 45, 693–702.CrossRefGoogle Scholar
Kang, W. & Sung, H. J. 2009 Large-scale structures of turbulent flows over an open cavity. J. Fluids Struct. 25, 1318–1333.Google Scholar
de Kat, R. 2012 Instantaneous planar pressure determination from particle image velocimetry. PhD dissertation, Delft University of Technology.Google Scholar
de Kat, R. & van Oudheusden, B. W. 2010 Instantaneous planar pressure from PIV: analytic and experimental test-cases. In 15th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, July 5–8, 2010.Google Scholar
de Kat, R. & van Oudheusden, B. W. 2012 Instantaneous planar pressure determination from PIV in turbulent flow. Exp Fluids 52, 1089–1106.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Knisely, C. & Rockwell, D. 1982 Self-sustained low-frequency components in an impinging shear layer. J. Fluid Mech. 116, 157–186.CrossRefGoogle Scholar
Kook, H., Mongeau, L., Brown, D. V. & Zorea, S. I. 1997 Analysis of the interior pressure oscillations induced by flow over vehicle openings. Noise Control Engng J. 45 (6), 223–234.Google Scholar
Koschatzky, V., Moore, P. D., Westerweel, J., Scarano, F. & Boersma, B. J. 2011 High speed PIV applied to aerodynamic noise investigation. Exp. Fluids 50, 863–876.Google Scholar
Lawson, S. J. & Barakos, G. N. 2011 Review of numerical simulations for high-speed, turbulent cavity flows. Prog. Aerosp. Sci. 47, 186–216.Google Scholar
Lee, S. B., Seena, A. & Sung, H. J. 2010 Self-sustained oscillations of turbulent flow in an open cavity. J. Aircraft. 47 (3), 820–834.Google Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Meneveau, C., Burns, R., Chen, S., Szalay, A. & Eyink, G. 2008 A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 9 (31).Google Scholar
Lighthill, M. J. 1963 Boundary layer theory. In Laminar Boundary Layers (ed. Rosenhead, L.). Oxford University Press.Google Scholar
Lin, J.-C. & Rockwell, D. 2001 Organized oscillations of initially turbulent flow past a cavity. AIAA J. 39, 1139–1151.Google Scholar
Liu, X. & Katz, J. 2006 Instantaneous pressure and material acceleration measurements using a four exposure PIV system. Exp. Fluids 41, 227–240.Google Scholar
Liu, X. & Katz, J. 2007 A comparison of cavitation inception index measurements to the spatial pressure distribution within a 2D cavity shear flow. FEDSM2007-37090. In 5th Joint ASME/JSME Fluids Engineering Conference, San Diego, California.Google Scholar
Liu, X. & Katz, J. 2008 Cavitation phenomena occurring due to interaction of shear layer vortices with the trailing corner of a 2D open cavity. Phys. Fluids 20, 041702.Google Scholar
Liu, X. & Katz, J. 2011a Time resolved PIV measurements elucidate the feedback mechanism that causes low-frequency undulation in an open cavity shear layer. In 9th International Symposium on Particle Image Velocimetry, PIV11, Kobe, Japan.Google Scholar
Liu, X. & Katz, J. 2011b Time resolved measurements of the pressure field generated by vortex-corner interactions in a cavity shear layer. AJK2011-08018. In ASME/JSME/KSME Joint Fluids Engineering Conference 2011, AJK2011-FED, Hamamatsu, Shizuoka, Japan.Google Scholar
Ma, R., Slaboch, P. E. & Morris, S. 2009 Fluid mechanics of the flow-excited Helmholtz resonator. J. Fluid Mech. 623, 1–26.Google Scholar
Martin, W. W., Naudascher, E. & Padmanabhan, M. 1975 Fluid-dynamic excitation involving flow instability. J. Hydr. Div. 101, 681–698.Google Scholar
Mathieu, J. & Scott, J. 2000 An Introduction to Turbulent Flow. Cambridge University press.Google Scholar
Moore, P., Lorenzoni, V. & Scarano, F. 2010 Two techniques for PIV-based aeroacoustic prediction and their application to a rod-aerofoil experiment. Exp. Fluids 20, 074005.Google Scholar
Morris, S. C. 2010 Shear-layer instabilities: particle image velocimetry measurements and implications for acoustics. Annu. Rev. Fluid Mech. 43, 529–550.Google Scholar
Najm, H. N. & Ghoniem, A. F. 1991 Numerical simulation of the convective instability in a dump combustor. AIAA J. 29 (6), 911–919.CrossRefGoogle Scholar
van Oudheusden, B. W. 2013 PIV-based pressure measurement. Meas. Sci. Technol. 24, 032001 (32pp).Google Scholar
Pereira, J. C. F. & Sousa, J. M. M. 1995 Experimental and numerical investigation of flow oscillations in a rectangular cavity. Trans. ASME J. Fluids Engng 117, 68–74.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Ragni, D., Ashok, A., van Oudheusden, B. W. & Scarano, F. 2009 Surface pressure and determination of a transonic aerofoil based on particle image velocimetry. Meas. Sci. 20, 074005.Google Scholar
Rockwell, D. 1983 Oscillations of impinging shear layers. AIAA J. 21 (5), 645–664.Google Scholar
Rockwell, D. 1998 Vortex-body interactions. Annu. Rev. Fluid Mech. 30, 199–229.Google Scholar
Rockwell, D. & Knisely, C. 1979 The organized nature of flow impingement upon a corner. J. Fluid Mech. 93, 413–432.Google Scholar
Rockwell, D. & Naudascher, E. 1978 Review: Self-sustaining oscillations of flow past cavities. J. Fluids Engng 100, 152–165.Google Scholar
Rockwell, D. & Naudascher, E. 1979 Self-sustained oscillations of impinging free shear layers. Annu. Rev. Fluid Mech. 11, 67–94.Google Scholar
Rossiter, J. E. 1964 Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. In Aeronautical Research Council Reports and Memoranda, No. 3438.Google Scholar
Roth, G. I. 1998 Developments in particle image velocimetry (PIV) and their application to the measurement of the flow structure and turbulence within a ship bow wave. PhD dissertation, Johns Hopkins University, Baltimore, MD.Google Scholar
Roth, G. I. & Katz, J. 2001 Five techniques for increasing the speed and accuracy of PIV interrogation. Meas. Sci. Technol. 12, 238–245.Google Scholar
Rowley, C. W. & Williams, D. R. 2006 Dynamics and control of high-Reynolds-number flow over open cavities. Annu. Rev. Fluid Mech. 38, 251–76.Google Scholar
Rowley, C. W., Williams, D. R., Colonius, T., Murray, R. M. & MacMynowski, D. G. 2006 Linear models for control of cavity flow oscillations. J. Fluid Mech. 547, 317–330.CrossRefGoogle Scholar
Sarohia, V. 1977 Experimental investigation of oscillations in flows over shallow cavities. AIAA J. 15 (7), 984–991.Google Scholar
Shams, E. & Apte, S. V. 2010 Prediction of small-scale cavitation in a high speed flow over an open cavity using large-eddy simulation. J. Fluids Engng 132, 111.Google Scholar
Takakura, Y., Higashino, F, Yoshizawa, T. & Ogawa, S. 1996 Numerical study on unsteady supersonic cavity flows. AIAA Paper 96-2092.Google Scholar
Tang, Y.-P. & Rockwell, D. 1983 Instantaneous pressure fields at a corner associated with vortex impingement. J. Fluid. Mech. 126, 187–204.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
van Oudheusden, B. W. 2008 Principles and application of velocimetry-based planar pressure imaging in compressible flows with shocks. Exp. Fluids 45, 657–674.Google Scholar
Violato, D., Moore, P. & Scarano, F. 2011 Lagrangian and Eulerian pressure field evaluation of rod-airfoil flow from time-resolved tomographic PIV. Exp. Fluids 50, 1057–1070.Google Scholar
Wei, T. & Willmarth, W. W. 1989 Reynolds-number effects on the structure of a turbulent channel flow. J. Fluid Mech. 204, 57–95.Google Scholar
Zaki, T. A & Saha, S. 2009 On shear sheltering and the structure of vortical modes in single- and two-fluid boundary layers. J. Fluid Mech. 626, 111–147.Google Scholar
Zhou, J., Adrian, R. J. & Balachandar, S. 1996 Autogeneration of near-wall vortical structures in channel flow. Phys. Fluids 8, 288–290.Google Scholar