Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T11:59:40.599Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex separation cascades in simulations of the planar flow past an impulsively started cylinder up to 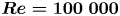$\boldsymbol{Re=100}\ \boldsymbol{000}$

Published online by Cambridge University Press:  20 December 2022

Michail Chatzimanolakis ,
Pascal Weber  and
Petros Koumoutsakos Open the ORCID record for Petros Koumoutsakos [Opens in a new window]
Michail Chatzimanolakis
Affiliation:
Computational Science and Engineering Laboratory, School of Engineering and Applied Sciences, Harvard University, 29 Oxford Street, MA 02138, USA Computational Science and Engineering Laboratory, Department of Mechanical and Process Engineering, ETH Zurich, Clausiusstrasse 33, 8051 Zurich, Switzerland
Pascal Weber
Affiliation:
Computational Science and Engineering Laboratory, School of Engineering and Applied Sciences, Harvard University, 29 Oxford Street, MA 02138, USA Computational Science and Engineering Laboratory, Department of Mechanical and Process Engineering, ETH Zurich, Clausiusstrasse 33, 8051 Zurich, Switzerland
Petros Koumoutsakos*
Affiliation:
Computational Science and Engineering Laboratory, School of Engineering and Applied Sciences, Harvard University, 29 Oxford Street, MA 02138, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations of the flow past an impulsively started cylinder at high Reynolds numbers (25k–100k) reveal an intriguing portrait of unsteady separation. Vorticity generation and vortex shedding entails a cascade of separation events on the cylinder surface that are reminiscent of Kelvin–Helmholtz instabilities. Primary vortices roll up along the cylinder surface as a result of instabilities of the initially attached vortex sheets, followed by vortex eruptions, creation of secondary vorticity and formation of dipole structures that are subsequently ejected from the surface of the cylinder. We analyse the vortical structures and their relationship to the forces experienced by the cylinder. This striking cascade of vortex instabilities may serve as reference for reduced-order models of flow separation and as guide for flow control of separated flows at high Reynolds numbers.

JFM classification

Wakes/Jets: Separated flows Vortex Flows: Vortex shedding Vortex Flows: Vortex dynamics
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 953 , 25 December 2022 , R2
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Almgren, A.S., Bell, J.B., Colella, P., Howell, L.H. & Welcome, M.L. 1998 A conservative adaptive projection method for the variable density incompressible Navier–Stokes equations. J. Comput. Phys. 142 (1), 1–46.CrossRefGoogle Scholar
Angot, P., Bruneau, C.H. & Fabrie, P. 1999 A penalization method to take into account obstacles in incompressible viscous flows. Numer. Math. 81 (4), 497–520.CrossRefGoogle Scholar
Bar-Lev, M. & Yang, H.T. 1975 Initial flow field over an impulsively started circular cylinder. J. Fluid Mech. 72 (4), 625–647.CrossRefGoogle Scholar
Bouard, R. & Coutanceau, M. 1980 The early stage of development of the wake behind an impulsively started cylinder for $40 < Re < 10^4$. J. Fluid Mech. 101 (3), 583–607.CrossRefGoogle Scholar
Chang, C.-C. & Chern, R.-L. 1991 Vortex shedding from an impulsively started rotating and translating circular cylinder. J. Fluid Mech. 233, 265–298.CrossRefGoogle Scholar
Chatzimanolakis, M., Weber, P. & Koumoutsakos, P. 2022 CubismAMR – a C++ library for distributed block-structured adaptive mesh refinement. arXiv:2206.07345v2.Google Scholar
Chorin, A.J. 1968 Numerical solution of the Navier–Stokes equations. Math. Comput. 22 (104), 745–762.CrossRefGoogle Scholar
Collins, W.M. & Dennis, S.C.R. 1973 Flow past an impulsively started circular cylinder. J. Fluid Mech. 60 (1), 105–127.CrossRefGoogle Scholar
Cottett, G.H. & Koumoutsakos, P. 2000 Vortex Methods: Theory and Applications. Cambridge University Press.CrossRefGoogle Scholar
Darakananda, D., Eldredge, J., Colonius, T. & Williams, D.R. 2016 A Vortex Sheet/Point Vortex Dynamical Model For Unsteady Separated Flows. AIAA Paper 2016-2072.CrossRefGoogle Scholar
van Dommelen, L. 1991 Lagrangian description of unsteady separation. Lect. Appl. Maths 28, 701–718.Google Scholar
Durante, D., Rossi, E., Colagrossi, A. & Graziani, G. 2017 Numerical simulations of the transition from laminar to chaotic behaviour of the planar vortex flow past a circular cylinder. Commun. Nonlinear Sci. Numer. Simul. 48, 18–38.CrossRefGoogle Scholar
Eldredge, J.D. 2019 Mathematical Modeling of Unsteady Inviscid Flows. Springer.CrossRefGoogle Scholar
Fleischmann, N., Adami, S. & Adams, N.A. 2019 Numerical symmetry-preserving techniques for low-dissipation shock-capturing schemes. Comput. Fluids 189, 94–107.CrossRefGoogle Scholar
Homa, J., Lucas, M. & Rockwell, D. 1988 Interaction of impulsively generated vortex pairs with bodies. J. Fluid Mech. 197, 571–594.CrossRefGoogle Scholar
Koumoutsakos, P. & Leonard, A. 1995 High-resolution simulations of the flow around an impulsively started cylinder using vortex methods. J. Fluid Mech. 296, 1–38.CrossRefGoogle Scholar
Kourta, A., Boisson, H.C., Chassaing, P. & Minh, H.H. 1987 Nonlinear interaction and the transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 181, 141–161.CrossRefGoogle Scholar
Li, Y., Shock, R., Zhang, R. & Chen, H. 2004 Numerical study of flow past an impulsively started cylinder by the lattice-Boltzmann method. J. Fluid Mech. 519, 273–300.CrossRefGoogle Scholar
Lighthill, M.J. 1963 Introduction. In Boundary Layer Theory (ed. J. Rosenhead), pp. 54–61. Oxford University Press.Google Scholar
Mittal, R., Dong, H., Bozkurttas, M., Najjar, F.M., Vargas, A. & von Loebbecke, A. 2008 A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 227 (10), 4825–4852.CrossRefGoogle ScholarPubMed
Orlandi, P. 1993 Vortex dipoles impinging on circular cylinders. Phys. Fluids A: Fluid Dyn. 5 (9), 2196–2206.CrossRefGoogle Scholar
Panton, R.L. 2013 Incompressible Flow. John Wiley and Sons.CrossRefGoogle Scholar
Pedley, T.J. 1983 Unsteady viscous flows. J. Fluid Mech. 137, 460–462.CrossRefGoogle Scholar
Prandtl, W. 1925 The Magnus effect and wind powered ships. Wissenschaften 13, 93–108.CrossRefGoogle Scholar
Quartapelle, L. & Napolitano, M. 1983 Force and moment in incompressible flows. AIAA J. 21 (6), 911–913.CrossRefGoogle Scholar
Rossinelli, D., Hejazi, B., Hadjidoukas, P., Bekas, C., Curioni, A., Bertsch, A., Futral, S., Schmidt, S., Adams, N. & Koumoutsakos, P. 2013 11 pflop/s simulations of cloud cavitation collapse. In International Conference for High Performance Computing, Networking, Storage and Analysis, SC.CrossRefGoogle Scholar
Rossinelli, D., Hejazialhosseini, B., van Rees, W., Gazzola, M., Bergdorf, M. & Koumoutsakos, P. 2015 MRAG-i2d: multi-resolution adapted grids for remeshed vortex methods on multicore architectures. J. Comput. Phys. 288, 1–18.CrossRefGoogle Scholar
Sheridan, J., Soria, J., Jie, W. & Welsh, M.C. 1993 The kelvin-helmholtz instability of the separated shear layer from a circular cylinder. In Bluff-Body Wakes, Dynamics and Instabilities (eds. H. Eckelmann, J. Michael, R. Graham, P. Huerre & P.A. Monkewitz), pp. 115–118. Springer.CrossRefGoogle Scholar
Singh, S.P. & Mittal, S. 2005 Flow past a cylinder: shear layer instability and drag crisis. Intl J. Numer. Meth. Fluids 47 (1), 75–98.CrossRefGoogle Scholar
Smith, P.A. & Stansby, P.K. 1988 Impulsively started flow around a circular cylinder by the vortex method. J. Fluid Mech. 194, 45–77.CrossRefGoogle Scholar
Ueda, Y. & Kida, T. 2021 Asymptotic analysis of initial flow around an impulsively started circular cylinder using a Brinkman penalization method. J. Fluid Mech. 929, A31.CrossRefGoogle Scholar
Vernet, J.A., Örlü, R. & Alfredsson, P.H. 2018 Flow separation control behind a cylindrical bump using dielectric-barrier-discharge vortex generator plasma actuators. J. Fluid Mech. 835, 852–879.CrossRefGoogle Scholar
Wu, C., Kinnas, S.A., Li, Z. & Wu, Y. 2019 A conservative viscous vorticity method for unsteady unidirectional and oscillatory flow past a circular cylinder. Ocean Engng 191, 106504.CrossRefGoogle Scholar

Chatzimanolakis et al. supplementary movie 1

Flow Past an Impulsively Started Cylinder at $\Rey=25~000$. Vorticity contours from $t=0$ to $t=20T$.
Download Chatzimanolakis et al. supplementary movie 1(Video)
Video 16.2 MB

Chatzimanolakis et al. supplementary movie 2

Flow Past an Impulsively Started Cylinder at $\Rey=50~000$. Vorticity contours from $t=0$ to $t=20T$..
Download Chatzimanolakis et al. supplementary movie 2(Video)
Video 22.3 MB

Chatzimanolakis et al. supplementary movie 3

Flow Past an Impulsively Started Cylinder at $\Rey=100~000$. Vorticity contours from $t=0$ to $t=20T$.

Download Chatzimanolakis et al. supplementary movie 3(Video)
Video 27.5 MB