Article contents
Vortex events in Euler and Navier–Stokes simulations with smooth initial conditions
Published online by Cambridge University Press: 23 November 2011
Abstract
We present high-resolution numerical simulations of the Euler and Navier–Stokes equations for a pair of colliding dipoles. We study the possible approach to a finite-time singularity for the Euler equations, and contrast it with the formation of developed turbulence for the Navier–Stokes equations. We present numerical evidence that seems to suggest the existence of a blow-up of the inviscid velocity field at a finite time (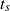 ) with scaling
) with scaling 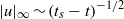 ,
, 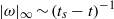 . This blow-up is associated with the formation of a
. This blow-up is associated with the formation of a 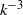 spectral range, at least for the finite range of wavenumbers that are resolved by our computation. In the evolution toward
spectral range, at least for the finite range of wavenumbers that are resolved by our computation. In the evolution toward 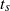 , the total enstrophy is observed to increase at a slower rate,
, the total enstrophy is observed to increase at a slower rate, 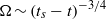 , than would naively be expected given the behaviour of the maximum vorticity,
, than would naively be expected given the behaviour of the maximum vorticity, 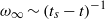 . This indicates that the blow-up would be concentrated in narrow regions of the flow field. We show that these regions have sheet-like structure. Viscous simulations, performed at various
. This indicates that the blow-up would be concentrated in narrow regions of the flow field. We show that these regions have sheet-like structure. Viscous simulations, performed at various 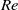 , support the conclusion that any non-zero viscosity prevents blow-up in finite time and results in the formation of a dissipative exponential range in a time interval around the estimated inviscid
, support the conclusion that any non-zero viscosity prevents blow-up in finite time and results in the formation of a dissipative exponential range in a time interval around the estimated inviscid 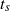 . In this case the total enstrophy saturates, and the energy spectrum becomes less steep, approaching
. In this case the total enstrophy saturates, and the energy spectrum becomes less steep, approaching 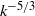 . The simulations show that the peak value of the enstrophy scales as
. The simulations show that the peak value of the enstrophy scales as 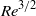 , which is in accord with Kolmogorov phenomenology. During the short time interval leading to the formation of an inertial range, the total energy dissipation rate shows a clear tendency to become independent of
, which is in accord with Kolmogorov phenomenology. During the short time interval leading to the formation of an inertial range, the total energy dissipation rate shows a clear tendency to become independent of 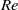 , supporting the validity of Kolmogorov’s law of finite energy dissipation. At later times the kinetic energy shows a
, supporting the validity of Kolmogorov’s law of finite energy dissipation. At later times the kinetic energy shows a 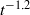 decay for all
decay for all 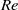 , in agreement with experimental results for grid turbulence. Visualization of the vortical structures associated with the stages of vorticity amplification and saturation show that, prior to
, in agreement with experimental results for grid turbulence. Visualization of the vortical structures associated with the stages of vorticity amplification and saturation show that, prior to 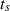 , large-scale and the small-scale vortical structures are well separated. This suggests that, during this stage, the energy transfer mechanism is non-local both in wavenumber and in physical space. On the other hand, as the spectrum becomes shallower and a
, large-scale and the small-scale vortical structures are well separated. This suggests that, during this stage, the energy transfer mechanism is non-local both in wavenumber and in physical space. On the other hand, as the spectrum becomes shallower and a 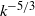 range appears, the energy-containing eddies and the small-scale vortices tend to be concentrated in the same regions, and structures with a wide range of sizes are observed, suggesting that the formation of an inertial range is accompanied by transfer of energy that is local in both physical and spectral space.
range appears, the energy-containing eddies and the small-scale vortices tend to be concentrated in the same regions, and structures with a wide range of sizes are observed, suggesting that the formation of an inertial range is accompanied by transfer of energy that is local in both physical and spectral space.
JFM classification
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 26
- Cited by


