Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-27T20:17:12.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex dynamics for flow around the slat cove at low Reynolds numbers

Published online by Cambridge University Press:  26 May 2021

Jiang-Sheng Wang  and
Jin-Jun Wang Open the ORCID record for Jin-Jun Wang [Opens in a new window]
Jiang-Sheng Wang
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beijing University of Aeronautics and Astronautics, Beijing100191, China
Jin-Jun Wang*
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beijing University of Aeronautics and Astronautics, Beijing100191, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

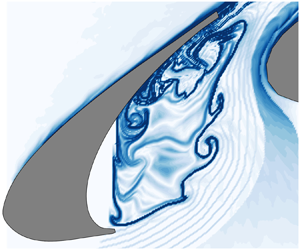
Time-resolved particle image velocimetry (TR-PIV) is employed to investigate the vortex dynamics around the slat cove of a 30P30N multi-element airfoil at a fixed geometric angle of attack of 4 ° within the stowed chord Reynolds number range of 9.3 × 103 ≤ Rec ≤ 5.2 × 104. The results link the frequency properties to the vortex shedding patterns of the slat cusp shear layer. With increasing Rec, three types of vortex dynamics are identified: (i) no vortex shedding from the slat cusp shear layer and the absence of hydrodynamic feedback in the slat cove (9.3 × 103 ≤ Rec ≤ 1.27 × 104); (ii) impingement of shed vortices on the underside of the slat trailing edge at a steady location (1.38 × 104 ≤ Rec ≤ 1.83 × 104); (iii) impingement of shed vortices on the underside of the slat trailing edge at unsteady locations (2.41 × 104 ≤ Rec ≤ 5.2 × 104). The fluctuations generated by shed vortices link the slat cusp and trailing edge by the hydrodynamic feedback in the slat cove. Besides the fundamental frequency and its harmonics, subharmonics and fractional harmonics occur to the slat cusp shear layer in the Rec range of 2.41 × 104–5.2 × 104. Subharmonics make the impingement locations of shed vortices unsteady. Fractional harmonics trigger the secondary instability of the braid region between two consecutive vortices to generate more shed vortices. The vortex dynamics in this Rec range is found to persist to Rec ~ 106.

JFM classification

Vortex Flows: Vortex interactions Vortex Flows: Vortex dynamics Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 919 , 25 July 2021 , A27
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agoropoulos, D. & Squire, L. 1988 Interactions between turbulent wakes and boundary layers. AIAA J. 26 (10), 1194–1200.CrossRefGoogle Scholar
Ashton, N., West, A. & Mendonça, F. 2016 Flow dynamics past a 30P30N three-element airfoil using improved delayed detached-eddy simulation. AIAA J. 54 (11), 3657–3667.CrossRefGoogle Scholar
Boutilier, M.S.H. & Yarusevych, S. 2012 Effects of end plates and blockage on low-Reynolds-number flows over airfoils. AIAA J. 50 (7), 1547–1559.CrossRefGoogle Scholar
Champagnat, F., Plyer, A., Le Besnerais, G., Leclaire, B., Davoust, S. & Le Sant, Y. 2011 Fast and accurate PIV computation using highly parallel iterative correlation maximization. Exp. Fluids 50 (4), 1169–1182.CrossRefGoogle Scholar
Choudhari, M. & Lockard, D.P. 2015 Assessment of slat noise predictions for 30P30N high-lift configuration from BANC-III workshop. AIAA Paper 2015-2844.CrossRefGoogle Scholar
Choudhari, M.M. & Khorrami, M.R. 2007 Effect of three-dimensional shear-layer structures on slat cove unsteadiness. AIAA J. 45 (9), 2174–2186.CrossRefGoogle Scholar
Deck, S. & Laraufie, R. 2013 Numerical investigation of the flow dynamics past a three-element aerofoil. J. Fluid Mech. 732, 401–444.CrossRefGoogle Scholar
Dobrzynski, W. 2010 Almost 40 years of airframe noise research: what did we achieve? J. Aircraft 47 (2), 353–367.CrossRefGoogle Scholar
Farge, M. 1992 Wavelet transforms and their applications to turbulence. Annu. Rev. Fluid Mech. 24 (1), 395–458.CrossRefGoogle Scholar
Haller, G. 2001 Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Physica D 149 (4), 248–277.CrossRefGoogle Scholar
Haller, G. & Yuan, G. 2000 Lagrangian coherent structures and mixing in two-dimensional turbulence. Physica D 147 (3), 352–370.CrossRefGoogle Scholar
He, G.-S., Pan, C., Feng, L.-H., Gao, Q. & Wang, J.-J. 2016 Evolution of Lagrangian coherent structures in a cylinder-wake disturbed flat plate boundary layer. J. Fluid Mech. 792, 274–306.CrossRefGoogle Scholar
Herr, M., Pott-Pollenske, M., Ewert, R., Boenke, D., Siebert, J., Delfs, J., Rudenko, A., Büscher, A., Friedel, H. & Mariotti, I. 2015 Large-scale studies on slat noise reduction. AIAA Paper 2015-3140.CrossRefGoogle Scholar
Imamura, T., Ura, H., Yokokawa, Y. & Yamamoto, K. 2009 A far-field noise and near-field unsteadiness of a simplified high-lift-configuration model (slat). AIAA Paper 2009-1239.CrossRefGoogle Scholar
Jawahar, H.K., Ali, S.A.S., Azarpeyvand, M. & da Silva, C.R.I. 2020 Aerodynamic and aeroacoustic performance of high-lift airfoil fitted with slat cove fillers. J. Sound Vib. 479, 115347.CrossRefGoogle Scholar
Jenkins, L.N., Khorrami, M.R. & Choudhari, M. 2004 Characterization of unsteady flow structures near leading-edge slat: part I. PIV measurements. AIAA Paper 2004-2801.CrossRefGoogle Scholar
Kegerise, M.A., Spina, E.F., Garg, S. & Cattafesta Iii, L.N. 2004 Mode-switching and nonlinear effects in compressible flow over a cavity. Phys. Fluids 16 (3), 678–687.CrossRefGoogle Scholar
Khorrami, M.R., Berkman, M.E. & Choudhari, M. 2000 Unsteady flow computations of a slat with a blunt trailing edge. AIAA J. 38 (11), 2050–2058.CrossRefGoogle Scholar
Kolb, A., Faulhaber, P., Drobietz, R. & Grünewald, M. 2007 Aeroacoustic wind tunnel measurements on a 2D high-lift configuration. AIAA Paper 2007-3447.CrossRefGoogle Scholar
Li, L., Liu, P.-Q., Guo, H., Hou, Y.-J., Geng, X. & Wang, J.-J. 2017 Aeroacoustic measurement of 30P30N high-lift configuration in the test section with Kevlar cloth and perforated plate. Aerosp. Sci. Technol. 70, 590–599.CrossRefGoogle Scholar
Li, L., Liu, P.-Q., Xing, Y. & Guo, H. 2018 a Time-frequency analysis of acoustic signals from a high-lift configuration with two wavelet functions. Appl. Acoust. 129, 155–160.CrossRefGoogle Scholar
Li, L., Liu, P., Xing, Y. & Guo, H. 2018 b Wavelet analysis of the far-field sound pressure signals generated from a high-lift configuration. AIAA J. 56 (1), 432–437.CrossRefGoogle Scholar
Lockard, D. & Choudhari, M. 2012 The influence of realistic Reynolds numbers on slat noise simulations. AIAA Paper 2012-2101.CrossRefGoogle Scholar
Mallat, S. 1999 A Wavelet Tour of Signal Processing. Elsevier.Google Scholar
Manoha, E. & Pott-Pollenske, M. 2015 LEISA2: an experimental database for the validation of numerical predictions of slat unsteady flow and noise. AIAA Paper 2015-3137.CrossRefGoogle Scholar
Morlet, J. 1983. Sampling theory and wave propagation. In Issues in Acoustic Signal/Image Processing and Recognition (ed. C.H. Chen), chap. 12, pp. 233–261. Springer.CrossRefGoogle Scholar
Murayama, M., Nakakita, K., Yamamoto, K., Ura, H., Ito, Y. & Choudhari, M.M. 2014 Experimental study of slat noise from 30P30N three-element high-lift airfoil in JAXA hard-wall low-speed wind tunnel. AIAA Paper 2014-2080.CrossRefGoogle Scholar
Olson, S., Thomas, F.O. & Nelson, R.C. 2001 Mechanisms of slat noise production in a 2D multi-element airfoil configuration. AIAA Paper 2156-2156.CrossRefGoogle Scholar
Pagani, C.C. Jr, Souza, D.S. & Medeiros, M.A. 2016 Slat noise: aeroacoustic beamforming in closed-section wind tunnel with numerical comparison. AIAA J. 54 (7), 2100–2115.CrossRefGoogle Scholar
Pagani, C.C., Souza, D.S. & Medeiros, M.A.F. 2017 Experimental investigation on the effect of slat geometrical configurations on aerodynamic noise. J. Sound Vib. 394, 256–279.CrossRefGoogle Scholar
Pan, C., Xue, D., Xu, Y., Wang, J.-J. & Wei, R.-J. 2015 Evaluating the accuracy performance of Lucas–Kanade algorithm in the circumstance of PIV application. Sci. China Phys. Mech. Astron. 58 (10), 1–16.CrossRefGoogle Scholar
Pascioni, K., Cattafesta, L.N. & Choudhari, M.M. 2014 An experimental investigation of the 30P30N multi-element high-lift airfoil. AIAA Paper 2014-3062.CrossRefGoogle Scholar
Pascioni, K.A. & Cattafesta, L.N. 2016 Aeroacoustic measurements of leading-edge slat noise. AIAA Paper 2016-2960.CrossRefGoogle Scholar
Pascioni, K.A. & Cattafesta, L.N. 2018 a An aeroacoustic study of a leading-edge slat: beamforming and far field estimation using near field quantities. J. Sound Vib. 429, 224–244.CrossRefGoogle Scholar
Pascioni, K.A. & Cattafesta, L.N. 2018 b Unsteady characteristics of a slat-cove flow field. Phys. Rev. Fluids 3 (3), 034607.CrossRefGoogle Scholar
Pott-Pollenske, M., Delfs, J. & Reichenberger, J. 2013 A testbed for large scale and high Reynolds number airframe noise research. AIAA Paper 2013-2260.CrossRefGoogle Scholar
Qu, Y., Wang, J.-J., Feng, L.-H. & He, X. 2019 Effect of excitation frequency on flow characteristics around a square cylinder with a synthetic jet positioned at front surface. J. Fluid Mech. 880, 764–798.CrossRefGoogle Scholar
Rossiter, J. 1964 Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. Tech. Rep. RM 3438. Aeronautical Research Council.Google Scholar
Shadden, S.C., Dabiri, J.O. & Marsden, J.E. 2006 Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids 18 (4), 047105.CrossRefGoogle Scholar
Smyth, W.D. 2003 Secondary Kelvin–Helmholtz instability in weakly stratified shear flow. J. Fluid Mech. 497, 67–98.CrossRefGoogle Scholar
Souza, D.S., Rodríguez, D., Himeno, F.H.T. & Medeiros, M.A.F. 2019 Dynamics of the large-scale structures and associated noise emission in airfoil slats. J. Fluid Mech. 875, 1004–1034.CrossRefGoogle Scholar
Squire, L. 1989 Interactions between wakes and boundary-layers. Prog. Aerosp. Sci. 26 (3), 261–288.CrossRefGoogle Scholar
Terracol, M., Manoha, E. & Lemoine, B. 2015 Investigation of the unsteady flow and noise generation in a slat cove. AIAA J. 54 (2), 469–489.CrossRefGoogle Scholar
Van Dam, C. 2002 The aerodynamic design of multi-element high-lift systems for transport airplanes. Prog. Aerosp. Sci. 38 (2), 101–144.CrossRefGoogle Scholar
Wang, J.-S., Feng, L.-H., Wang, J.-J. & Li, T. 2018 Görtler vortices in low-Reynolds-number flow over multi-element airfoil. J. Fluid Mech. 835, 898–935.CrossRefGoogle Scholar
Wang, J.-S., Wang, J.-J. & Kim, K.-C. 2019 Wake/shear layer interaction for low-Reynolds-number flow over multi-element airfoil. Exp. Fluids 60 (1), 1–24.CrossRefGoogle Scholar
Welch, P. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15 (2), 70–73.CrossRefGoogle Scholar
Zhang, Y.-F., Chen, H.-X., Wang, K. & Wang, M. 2017 Aeroacoustic prediction of a multi-element airfoil using wall-modeled large-eddy simulation. AIAA J. 55 (12), 4219–4233.CrossRefGoogle Scholar