Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-21T16:12:07.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex development behind a finite porous obstruction in a channel

Published online by Cambridge University Press:  06 December 2011

Lijun Zong  and
Heidi Nepf
Lijun Zong*
Affiliation:
48-216, Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Heidi Nepf
Affiliation:
48-216, Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

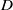This experimental study describes the turbulent wake behind a two-dimensional porous obstruction, consisting of a circular array of cylinders. The cylinders extend from the channel bed through the water surface, mimicking a patch of emergent vegetation. Three patch diameters () and seven solid volume fractions (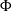) are tested. Because flow can pass through the patch, directly downstream there is a region of steady, non-zero, streamwise velocity, 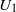, called the steady wake. For the patch diameters and solid volume fractions considered here, 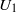is a function of 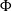only. The length of the steady wake (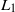) increases as decreases and can be predicted from the growth of a plane shear layer. The formation of the von-Kármán vortex street is delayed until the end of the steady wake. There are two regions of elevated transverse velocity fluctuation (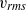): directly behind the patch, associated with the wake turbulence of individual cylinders; and at the distance 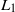from the patch, associated with the formation of large-scale wake oscillation. Velocity along the centreline of the wake starts to increase only after the patch-scale vortex street is formed, and it approaches the free-stream velocity over a distance . The dimensionless length of the entire wake, 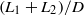, increases with patch porosity.

JFM classification

Wakes/Jets: Shear layers Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 691 , 25 January 2012 , pp. 368 - 391
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ball, D. J., Stansby, P. K. & Alliston, N. 1996 Modelling shallow water flow around pile groups. Proc. Inst. Civ. Engrs Wat., Marit. Energy 118, 226–236.Google Scholar
2. Bearman, P. W. 1965 Investigation of the flow behind a two-dimensional model with a blunt trailing edge and fitted with splitter plates. J. Fluid Mech. 21 (2), 241–255.Google Scholar
3. Bouma, T., Van Duren, L., Temmerman, S., Claverie, T., Blanco-Garcia, A., Ysebaert, T. & Herman, P. 2007 Spatial flow and sedimentation patterns within patches of epibenthic structures: combining field, flume and modelling experiments. Cont. Shelf Res. 27, 1020–1045.Google Scholar
4. Brookshire, E. & Dwire, K. 2003 Controls on patterns of coarse organic particle retention in headwater streams. J. N. Am. Benth. Soc. 22, 17–34.Google Scholar
5. Cantwell, B. & Coles, D. 1983 An experimental study of entrainment and transport in the turbulent near wake of a circular cylinder. J. Fluid Mech. 136, 321–374.CrossRefGoogle Scholar
6. Castro, I. P. 1971 Wake characteristics of two-dimensional perforated plates normal to an air-stream. J. Fluid Mech. 46 (3), 599–609.Google Scholar
7. Champagne, F. H., Pao, Y. H. & Wygnanski, I. J. 1976 On the two-dimensional mixing region. J. Fluid Mech. 74, 209–250.Google Scholar
8. Chen, D. & Jirka, G. H. 1995 Experimental study of plane turbulent wakes in a shallow water layer. Fluid Dyn. Res. 16, 11–41.Google Scholar
9. Chen, J. H., Pritchard, W. H. & Tavener, S. J. 1995 Bifurcation for flow past a cylinder between parallel planes. J. Fluid Mech. 284, 23–41.Google Scholar
10. Cotton, J., Wharton, G., Bass, J., Heppell, C. & Wotton, R. 2006 The effects of seasonal changes to in-stream vegetation cover on patterns of flow and accumulation of sediment. Geomorphology 77, 320–334.Google Scholar
11. Coutanceau, M. & Bouard, R. 1977 Experimental determination of the main features of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow. J. Fluid Mech. 79, 231–256.Google Scholar
12. Dimotakis, P. E. 1991 Turbulent free shear layer mixing and combustion. In High-Speed Flight Propulsion Systems (ed. Murthy, S. N. B. & Curran, E. T. ), pp. 265–340. AIAA.Google Scholar
13. Fonseca, M., Zieman, J., Thayer, G. & Fisher, J. 1983 The role of current velocity in structuring eelgrass meadows. Estuar. Coast. Shelf Sci. 17, 367–380.Google Scholar
14. Gacia, E. & Duarte, C. 2001 Sediment retention by a Mediterranean Posidonia oceanica meadow: the balance between deposition and resuspension. Estuar. Coast. Shelf. Sci. 52 (4), 505–514.CrossRefGoogle Scholar
15. Huang, Z. & Keffer, J. F. 1996 Development of structure within the turbulent wake of a porous body. Part 1. The initial formation region. J. Fluid Mech. 329, 103–115.Google Scholar
16. Kravchenko, A. G. & Moin, P. 1999 Numerical studies of flow over a circular cylinder at . Phys. Fluids 12 (2), 403–417.CrossRefGoogle Scholar
17. Lopez, F. & Garcia, M. 1998 Open-channel flow through simulated vegetation: suspended sediment transport modelling. Water Resour. Res. 34 (9), 2341–2352.Google Scholar
18. Lyn, D. A., Einav, S., Rodi, W. & Park, J.-H. 1995 A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder. J. Fluid Mech. 304, 285–319.Google Scholar
19. Moore, K. A. 2004 Influence of seagrasses on water quality in shallow regons of the lower Chesapeake bay. J. Coast. Res. 20, 162–178 (special issue).Google Scholar
20. Nepf, H. 1999 Drag, turbulence and diffusivity in flow through emergent vegetation. Water Resour. Res. 35 (2), 479–489.Google Scholar
21. Nicolle, A. & Eames, I. 2011 Numerical study of flow through and around a circular array of cylinders. J. Fluid Mech. 679, 1–31.Google Scholar
22. Norberg, C. 1994 An experimental investigation of the flow around a circular cylinder: influence of aspect ratio. J. Fluid Mech. 258, 287–316.Google Scholar
23. Rominger, J., Lightbody, A. & Nepf, H. 2010 The effects of added vegetation on sand bar stability and stream hydrodynamics. J. Hydraul. Engng 136 (12), 944.Google Scholar
24. Rominger, J. & Nepf, H. 2011 Flow adjustment and interior flow associated with a rectangular porous obstruction. J. Fluid Mech. 680, 636–659.Google Scholar
25. Roshko, A. 1961 Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 10, 345–356.Google Scholar
26. Sahin, M. & Owens, R. G. 2004 A numerical investigation of wall effects up to high blockage ratios on two-dimensional flow past a confined circular cylinder. Phys. Fluids 16 (5), 1305–1320.CrossRefGoogle Scholar
27. Sand-Jensen, K. & Pedersen, M. L. 2008 Streamlining of plant patches in streams. Freshwat. Biol. 53, 714–726.Google Scholar
28. Schewe, G. 1983 On the force fluctuation acting on a circular cylinder in cross-flow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech. 133, 265–285.Google Scholar
29. Schultz, M., Kozerski, H.-P., Pluntke, T. & Rinke, K. 2003 The influence of macrophytes on sedimentation and nutrient retention in the lower river spree. Water Resour. Res. 37, 569–578.Google Scholar
30. Sharpe, R. G. & James, C. S. 2006 Deposition of sediment from suspension in emergent vegetation. Water SA 32 (2), 211–218.Google Scholar
31. Stone, B. & Shen, H. T. 2002 Hydraulic resistance of flow in channels with cylindrical roughness. J. Hydraul. Engng ASCE 128 (5), 500–506.Google Scholar
32. Takemura, T. & Tanaka, N. 2007 Flow structures and drag characteristics of a colony-type emergent roughness model mounted on a flat plate in uniform flow. Fluid Dyn. Res. 39, 694.Google Scholar
33. Tanino, Y. & Nepf, H. 2008 Lateral dispersion in random cylinder arrays at high Reynolds number. J. Fluid Mech. 600, 339–371.Google Scholar
34. Townsend, A. A. 1947 Measurements in the turbulent wake of a cylinder. Proc. R. Soc. Lond. A 190, 551–561.Google Scholar
35. Turki, S., Abbassi, H. & Nasrallah, S. B. 2003 Effect of the blockage ratio on the flow in a channel with a built-in square cylinder. Comput. Mech. 33, 22–29.Google Scholar
36. White, B. & Nepf, H. 2007 Shear instability and coherent structures in a flow adjacent to a porous layer. J. Fluid Mech. 593, 1–32.Google Scholar
37. White, B. & Nepf, H. 2008 A vortex-based model of velocity and shear stress in a partially vegetated shallow channel. Water Resour. Res. 44, W01412.Google Scholar
38. Windham, L., Weis, J. & Weis, P. 2003 Uptake and distribution of metals in two dominant salt marsh macrophytes, Spartina alterniflora and Phragmites australis . Estuar. Coast. Shelf Sci. 56, 63–72.Google Scholar
39. Widdows, J., Pope, N. & Brinsley, M. 2008 Effect of Spartina anglicastems on near-bed hydrodynamics, sediment erodability, and morphological changes on an intertidal mudflat. Mar. Ecol. Progr. Ser. 362, 45–57.Google Scholar
40. Wood, C. J. 1967 Visualization of an incompressible wake with base bleed. J. Fluid Mech. 29, 259–272 Part 2.Google Scholar
41. Zong, L. & Nepf, H. 2011 Spatial distribution of deposition within a patch of vegetation. Water Resour. Res. 47, W03516.Google Scholar