Viscous Marangoni migration of an inviscid bubble by surfactant spreading: an exactly solvable model

Abstract

A model is formulated of a two-dimensional migrating, or swimming, inviscid bubble in a viscous fluid whose unsteady displacement is caused by the spreading over its surface of an initial distribution of insoluble surfactant. Assuming small capillary and Reynolds numbers, and a linear equation of state giving the surface tension as a function of surfactant concentration, the quasi-steady Stokes flow around the bubble is found analytically and explicit formulas are determined for the time-dependent bubble speed and its final overall displacement. At infinite surface Péclet number this is done using a complex version of the method of characteristics to solve a complex partial differential equation of Burgers type. For a finite non-zero surface Péclet number, the problem is shown to be linearizable by a complex variant of the classical Cole–Hopf transformation. The formulation allows general statements to be made on the bubble speed and its total net displacement in terms of the initial surfactant distribution. A weak finite-time singularity in the surface activity associated with an isolated clean point on the bubble surface is also identified and studied in detail.

1. Introduction

The study of propulsion mechanisms of small objects, organisms, swimmers or particles at low Reynolds numbers is a highly active area of current research (Nakata et al. 2015; Zöttl & Stark 2016; Suematsu & Nakata 2018; Michelin 2023). One mechanism whereby self-propulsion can be achieved is by the setting up of a Marangoni stress on an interface. This commonly involves an object, or ‘Marangoni surfer’ (Lauga & Davis 2011; Würger 2014; Crowdy 2020, 2021a; Dietrich et al. 2020), leveraging the benefit of its location at an interface between two fluids to release surfactants that cause a surface tension gradient, and a concomitant Marangoni stress, leading to locomotion. This phenomenon occurs in natural biological settings (Bush & Hu 2006) and has also been exploited in synthetic situations (Nakata et al. 2015; Suematsu & Nakata 2018). Several analytical models have been devised providing a theoretical understanding of this mode of locomotion in the viscous regime when surface diffusion of surfactant is dominant (Lauga & Davis 2011; Crowdy 2020, 2021a).

A closely related paradigm is the study of swimming droplets. A recent review (Maass et al. 2016) gives an overview of microswimmers based on liquid droplets where the propulsion mechanism does not require the presence of a separate interface or the imposition of some global external influence such as an imposed temperature gradient (Young, Goldstein & Block 1959). It is also known that isotropic droplets, with no intrinsic asymmetry, can move spontaneously due to a nonlinear coupling between the transport of a solute with self-generated Marangoni flows. Michelin (2023) has surveyed the recent results in this area. Typically, a droplet becomes active, and consequently self-propelling, due to a chemical reaction (Schmitt & Stark 2013), micelle-induced solubilization or a phase transition (Maass et al. 2016).

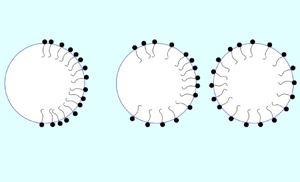
This paper presents an analytical study of unsteady bubble propulsion referred to here as viscous Marangoni migration by surfactant spreading. This mode of locomotion is illustrated in figure 1 where three time snapshots of a swimming bubble are shown. The model to be analysed is a two-dimensional inviscid bubble embedded in unbounded viscous fluid where some distribution of insoluble surfactant is set up on the bubble surface at some initial instant. Mathematically, this is an initial-value problem. How this initial distribution might be set up is not discussed here but if, as indicated in figure 1, there is an initial surplus of surfactant molecules on the right-hand side of the bubble the Marangoni stresses associated with its advective–diffusive spreading around the surface cause a Stokes flow in the surrounding viscous fluid and a net migration of the bubble to the right. This is because at zero Reynolds number the bubble must be free of net force and torque. The challenge is to determine the speed $U_B(t)$ of the bubble and its final net displacement $\Delta x$. Although any net locomotion relies on a breaking of symmetry in the initial surfactant distribution, the mechanism is intrinsically nonlinear because it depends on the advective–diffusive spreading of surfactant over the bubble surface. It is also inherently transient, perhaps more accurately described as bubble ‘hopping’ rather than ‘swimming’, because the migration is arrested as soon as the surfactant has spread to a uniform distribution. Further displacement can be envisaged by a repeat of this basic protocol, with more hops induced by a renewing of the initial left–right asymmetric surfactant distribution. Of course, such a strategy might be impeded by familiar short-lifetime challenges due to the loss of the surface tension gradient unless suitable surface reaction effects are also at work (Cheng et al. 2019). Such concerns are beyond the scope of this article.

Figure 1. Three snapshots of the unsteady migration of a single bubble due to an initial distribution of insoluble surfactant set up at $t=0$ which subsequently spreads around the surface. The motion is arrested when the distribution is uniform. The challenge is to determine the speed of the bubble $U_B(t)$ and its net displacement $\Delta x$.

The proposed basic mechanism is reminiscent of the strategic release of surfactant by insects, such as Microvelia, at interfaces to propel themselves along (Bush & Hu 2006) although, in the case of a swimming bubble, it carries its own proprietary interface that travels with it, more akin to an insect's plastron. Tsemakh, Lavrenteva & Avinoam (2004) have studied the swimming of a droplet in a viscous fluid due to Marangoni stresses set up at its surface due to the uniform secretion of a surface-active substance from a contained droplet placed off-centre inside the mother droplet. Mass transfer of this substance causes a surface Marangoni stress on the compound mother droplet that leads to net migration. Modern embodiments of similar ideas involving compound droplets of this kind but with different actuation mechanisms have been proposed by Ganesh et al. (2023).

Despite the nonlinear nature of the multiphysics problem in figure 1, the present study demonstrates that a two-dimensional model of such bubble migration can be solved in analytical form at any value of the surface Péclet number. The model makes a number of physically reasonable assumptions: that the Reynolds and capillary numbers are small, that a linear equation of state determines the surface tension as a function of the surfactant concentration and that the bubble dynamics is governed by nonlinear advection–diffusion of the insoluble surfactant on the bubble boundary leading to unsteady Marangoni stresses that determine a quasi-steady Stokes flow in the surrounding fluid.

Analytical solutions are possible because of a theoretical connection, elucidated here, between Marangoni dynamics and a complex form of the Burgers equation (Crowdy 2021b,c). The latter is a nonlinear partial differential equation familiar to fluid dynamicists in its real version by virtue of its appearance in models of one-dimensional compressible gas dynamics (Whitham 1999). Indeed, the formulation here is a generalization, to the radial bubble geometry, of work by Crowdy (2021b,c) who showed that, under the same modelling assumptions just listed, insoluble surfactant dynamics on the surface of a half-plane region of viscous fluid can be described by a complex Burgers equation at arbitrary surface Péclet number. Although the mathematical details are different, the main theoretical ramifications of that prior work carry over to the bubble geometry. Arguably the most significant implication is that the nonlinear swimming bubble problem of interest here can be linearized at any non-zero surface Péclet number by a complex-valued variant of the classical Cole–Hopf transformation (Whitham 1999; Crowdy 2021b,c).

Although the model is limited in its physical relevance in being two-dimensional, its amenability to closed-form analytical solution renders it valuable in exemplifying fundamental physical mechanisms in mathematical form. Several theoretical studies on two-dimensional swimming droplets have similarly been of value in providing insights into basic effects (Hu et al. 2019; Li 2022).

2. Bubble migration by surfactant spreading

A circular, two-dimensional, inviscid, incompressible bubble of radius ${\mathcal {R}}$ is initially centred on the $x$ axis in an $(x,y)$ plane and is surrounded by unbounded fluid of viscosity $\mu$. The bubble has constant pressure $p_B$. It is assumed that, at $t=0$, there is some mechanism that instantaneously sets up an initial concentration $\varGamma (s,0) = \varGamma _0(s)$ of surfactant on the bubble boundary, taken to be symmetric about the diameter along the $x$ axis, where $s$ is arclength in the boundary tangent direction taken clockwise around the bubble boundary. The assumption of symmetry about the $x$ axis is not necessary, but it simplifies the analysis and statement of the main results. All that follows can be generalized if this assumption is relaxed.

The surfactant is assumed to be insoluble to the bulk fluid but can be advected around the bubble surface and diffuses along it with surface diffusion coefficient $D_s$. The surfactant affects the local surface tension $\sigma (s,t)$ according to the linear equation of state

(2.1)\begin{equation} \sigma(s,t) = \sigma_c - \beta \varGamma(s,t), \end{equation}

where $\sigma _c$ is the clean-flow surface tension and $\beta = RT$, where $T$ is absolute temperature, assumed to be constant, and $R$ is the gas constant. A capillary number, to be introduced later, based on the clean-flow surface tension $\sigma _c$ is assumed small so that the bubble can be taken to remain circular and undeformed at leading order. An initial concentration of surfactant such as that shown in figure 1 will spread around the bubble causing a time-dependent Marangoni stress on its boundary. As a result, the bubble is expected to move in the $x$ direction with some time-dependent speed $U_B(t)$. Since the motion is arrested when the surfactant distribution has spread out to become uniform, the bubble will ultimately, at large times, be displaced by some finite distance $\Delta x$ from its starting point. The aim of this paper is to determine the bubble speed $U_B(t)$ and total bubble displacement $\Delta x$ as a function of the initial surfactant concentration profile.

It is natural to move to a bubble-fixed frame of reference co-travelling with the bubble at each instant with speed $U_B(t)$ that is unknown a priori. Assuming a Reynolds number based on $U_B$, ${\mathcal {R}}$ and $\mu$ is sufficiently small, the fluid velocity $\boldsymbol {u}=(u,v)$ outside the bubble in this frame can be taken to satisfy the incompressible quasi-steady Stokes equations

(2.2a,b)\begin{equation} {-} \boldsymbol{\nabla} p + \mu \nabla^2 \boldsymbol{u} = 0, \quad \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u} = 0, \end{equation}

where $p(x,y,t)$ is the fluid pressure. The unit tangent $\boldsymbol {t}$ and normal $\boldsymbol {n}$ vectors are indicated in figure 2; note that $\boldsymbol {t}$ is directed clockwise around the boundary while $\boldsymbol {n}$ points into the viscous fluid from the bubble. A kinematic condition on the bubble boundary is

(2.3)\begin{equation} \boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{n} = 0. \end{equation}

This states that the boundary must be a streamline in the co-travelling frame. The stress balance on the bubble boundary is

(2.4)\begin{equation} {-} (p-p_B) n_i + 2 \mu e_{ij} n_j = \frac{\sigma}{{\mathcal{R}}} n_i - \frac{\partial \sigma }{\partial s} t_i, \end{equation}

where $n_i$ and $t_i$ denote the $i$th components of $\boldsymbol {n}$ and $\boldsymbol {t}$, respectively, and $e_{ij}$ is the usual fluid rate-of-strain tensor. The second term on the right-hand side of (2.4) represents the Marangoni stress caused by the varying surface tension. The surface tension $\sigma (s,t)$ is given by (2.1) where $\varGamma (s,t)$ satisfies the surfactant evolution equation which, in a frame of reference co-moving with the fixed-shape bubble, is (Wong, Rumschitzki & Maldarelli 1996)

(2.5)\begin{equation} \frac{\partial \varGamma(s,t) }{\partial t} + \frac{\partial (\varGamma(s,t) U(s,t)) }{\partial s} = {D_s} \frac{\partial^2 \varGamma(s,t) }{\partial s^2}, \end{equation}

where $U(s,t)$ is the surface slip velocity in the tangential direction. On integrating (2.5) around the entire bubble boundary it follows that the average surfactant concentration over the interface, denoted by $\langle {\varGamma _0} \rangle$, is a constant of the motion, namely

(2.6)\begin{equation} \langle {\varGamma_0} \rangle \equiv \frac{1 }{2{\rm \pi} {\mathcal{R}}} \int_{-{\rm \pi} {\mathcal{R}}}^{ {\rm \pi}{\mathcal{R}}} \varGamma_0(s) \,{\rm d} s = \frac{1 }{2{\rm \pi} {\mathcal{R}}} \int_{-{\rm \pi} {\mathcal{R}}}^{ {\rm \pi}{\mathcal{R}}} \varGamma(s,t) \,{\rm d} s, \end{equation}

where it is convenient to take $s=0$ to correspond to the front of the bubble at $x={\mathcal {R}}$ on the positive $x$ axis. The condition on the fluid velocity in the far field is

(2.7)\begin{equation} \boldsymbol{u} \to ({-}U_B(t),0) \quad {\rm as} \ |\boldsymbol{x}| \to \infty, \end{equation}

where the condition that the bubble is free of net force determines $U_B(t)$. The assumed reflectional symmetry of the initial surfactant concentration about the $x$ axis through the bubble centre is expected to be dynamically preserved and ensures zero net torque on it.

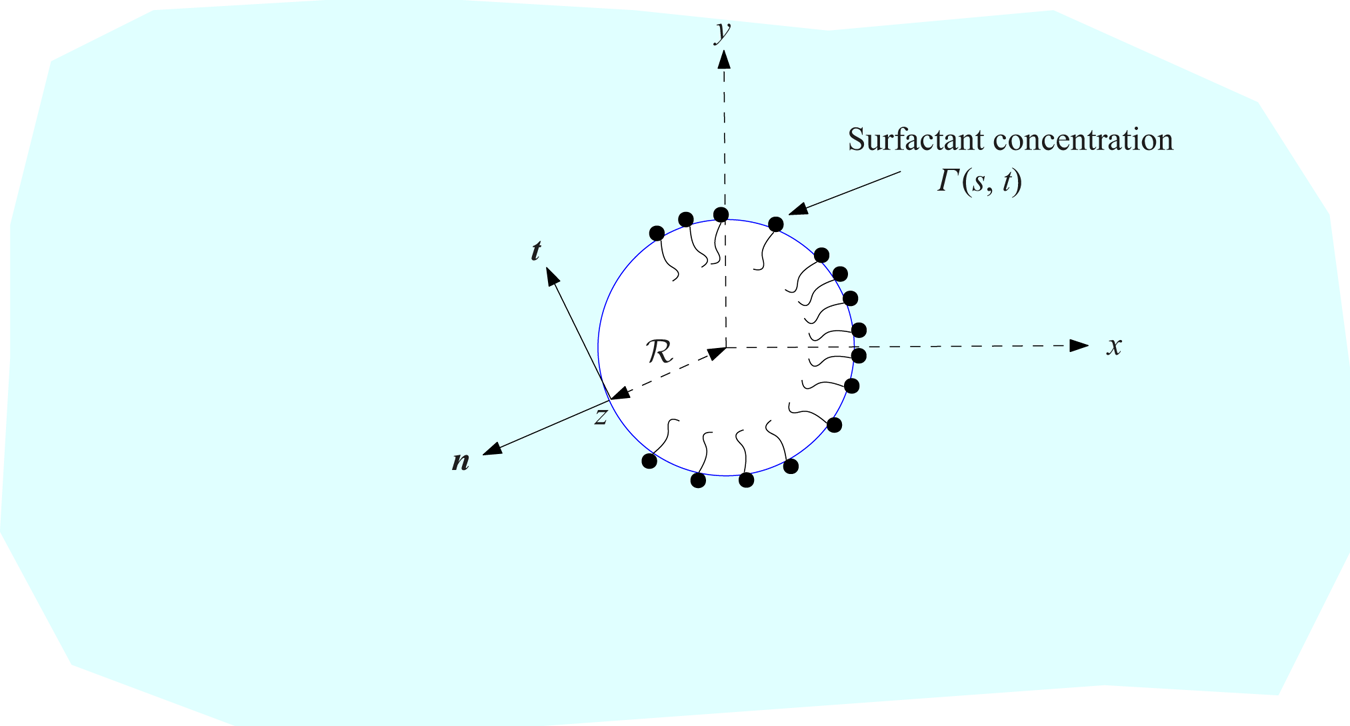
Figure 2. A circular bubble of radius ${\mathcal {R}}$ in a complex $z=x+{\rm i} y$ plane. If $z$ is a point on the bubble boundary the complex analogue of the unit normal vector $\boldsymbol {n}$ is $z/{\mathcal {R}}$ and the complex analogue of the unit tangent vector $\boldsymbol {t}$ is $-{\rm i}(z/{\mathcal {R}})$. The arclength $s$ increases in the direction of $\boldsymbol {t}$.

Unless surface diffusion of surfactant is dominant, this multiphysics problem constitutes a nonlinear system where the surface advection–diffusion of the surfactant determines the instantaneous Stokes flow in the bulk which, in turn, feeds back to affect the surfactant advection on the moving bubble.

3. Complex variable formulation

The flow generated by the surfactant evolution will be found using a complex variable formulation of two-dimensional, quasi-steady Stokes flow of which an appendix of Crowdy (2020) gives a brief derivation. On taking the curl of the Stokes equations (2.2) and introducing a streamfunction $\psi$ associated with the incompressible two-dimensional flow,

(3.1)\begin{equation} \boldsymbol{u} = (u,v) = \left ( \frac{\partial \psi }{\partial y}, -\frac{\partial \psi }{\partial x} \right ) , \end{equation}

it can be shown that $\psi$ satisfies the biharmonic equation in the fluid region, namely

(3.2a,b)\begin{equation} \nabla^4 \psi = 0, \quad \nabla^2 = \frac{\partial^2 }{\partial x^2} + \frac{\partial^2 }{\partial y^2}. \end{equation}

On letting $z=x +{\rm i}y$ this partial differential equation can be written as

(3.3)\begin{equation} \frac{\partial^4 \psi }{\partial z^2 \partial \bar{z}^2} = 0, \end{equation}

which can be integrated (Crowdy 2020) leading to a general representation of a real-valued biharmonic streamfunction given by

(3.4)\begin{equation} \psi = \psi(z,\bar{z},t) = {\rm Im}[\bar{z}f(z,t) + g(z,t)], \end{equation}

where ${\rm Im}[\cdot ]$ denotes the imaginary part of the complex quantity in square brackets and $f(z,t)$ and $g(z,t)$ are complex potentials, also known as Goursat functions. In general, all singularities of these analytic functions must be inside the bubble, or at infinity, and not in the viscous fluid. Moreover, a logarithmic singularity of $f(z,t)$ inside the bubble can be identified with a Stokeslet singularity implying a non-zero net force on the bubble while a logarithmic singularity of $g(z,t)$ inside the bubble can be identified with a rotlet singularity implying a non-zero net torque on it. Since, in the present problem, the bubble is free of net force and torque, both $f(z,t)$ and $g(z,t)$ will be analytic and single-valued in the viscous fluid region. This is explained in more detail in what follows.

It can be shown (Crowdy 2020) that $p(x,y,t)$, the vorticity $\omega = -\nabla ^2 \psi$ and the fluid rate-of-strain tensor $e_{ij}$ are related to $f(z,t)$ and $g(z,t)$ through the relations

(3.5)\begin{equation} \left.\begin{array}{@{}c@{}} 4f'(z,t) = \dfrac{p }{\mu} - {\rm i} \omega, \quad u - {\rm i} v ={-} \overline{f(z,t)} + \bar{z} {f'(z,t)} + {g'(z,t)} , \\ e_{11} + {\rm i} e_{12} = z \overline{f''(z,t)} +\overline{g''(z,t)}, \end{array}\right\} \end{equation}

where overbars denote complex conjugation and the prime notation denotes partial differentiation with respect to $z$. There is an additive degree of freedom in the choice of $f(z,t)$ and $g'(z,t)$ since if $f(z,t)$ is changed to $f(z,t) + c(t)$ and $g'(z,t)$ is changed to $g'(z,t) + \overline {c(t)}$, where $c(t)$ is a complex function of time, then the complex velocity field $u-\textrm {i}v$ given in (3.5) is unaltered. This degree of freedom is eliminated shortly.

The complex form of the fluid stress at the boundary, or $-p n_i + 2 \mu e_{ij}n_j$, is (Crowdy 2020)

(3.6a,b)\begin{equation} {-} 2 \mu {\rm i} \frac{\partial H }{\partial s}, \quad H(z,\bar{z},t) \equiv f(z,t) + z \overline{f'(z,t)} + \overline{g'(z,t)}. \end{equation}

Since there is no net force on the bubble then integration of the fluid stress (3.6) with respect to arclength around its boundary must give zero. This means that $H(z,\bar {z},t)$ must be single-valued around the bubble. The single-valuedness of $f(z,t$) around the bubble then follows on noticing, from (3.5) and (3.6), that $H(z,\bar {z},t) = 2f(z,t)+ (u+\textrm {i}v)$ and bearing in mind that $u+\textrm {i} v$ is necessarily single-valued around the bubble.

On rearrangement, the stress condition (2.4) on the bubble boundary can be written as

(3.7)\begin{equation} {-}p n_i + 2 \mu e_{ij} n_j = \frac{\sigma }{{\mathcal{R}}} n_i - \frac{\partial \sigma }{\partial s} t_i - p_B n_i, \end{equation}

which will now be written in complex form. For this, note that the complex form of the unit tangent vector is

(3.8)\begin{equation} \frac{{\rm d}z }{{\rm d}s} ={-} \frac{{\rm i} z }{{\mathcal{R}}} \end{equation}

and the complex form of the unit normal vector is

(3.9)\begin{equation} {\rm i} \frac{{\rm d} z }{{\rm d}s} = \frac{z }{{\mathcal{R}}}. \end{equation}

Consequently, the complex variable statement of (3.7) is

(3.10)\begin{align} - 2 \mu {\rm i} \frac{\partial H }{\partial s} &= \frac{\sigma }{{\mathcal{R}}} {\rm i} \frac{{\rm d}z }{{\rm d}s} - \frac{\partial \sigma }{\partial s} \frac{{\rm d}z }{{\rm d}s} - p_B {\rm i} \frac{{\rm d} z }{{\rm d}s} = \frac{{\rm i} \sigma }{{\mathcal{R}}} \frac{{\rm d}z }{{\rm d}s} + \frac{\partial \sigma }{\partial s} \frac{{\rm i} z }{{\mathcal{R}}} - p_B {\rm i} \frac{{\rm d} z }{{\rm d}s}\nonumber\\ & = \frac{{\rm i} }{{\mathcal{R}}} \frac{\partial (\sigma z) }{\partial s} - p_B {\rm i} \frac{{\rm d} z }{{\rm d}s}, \end{align}

where (3.6), (3.8) and (3.9) have been used. This can be integrated with respect to $s$ to give

(3.11)\begin{equation} {-} 2 \mu H(z, \bar{z},t) = \frac{\sigma z }{{\mathcal{R}}} - p_B z, \end{equation}

where an additive function of time has been set to zero without loss of generality by exploiting the aforementioned additive degree of freedom in the choice of $f(z,t)$ and $g'(z,t)$. On use of the equation of state (2.1), (3.11) implies that

(3.12)\begin{equation} \frac{H(z, \bar{z},t) }{z} = \frac{\beta \varGamma }{2\mu {\mathcal{R}}} + \frac{1 }{2\mu} \left (p_B - \frac{\sigma_c }{{\mathcal{R}}} \right ). \end{equation}

The next step is to introduce the decompositions

(3.13a,b) \begin{equation} f(z,t) = \frac{p_H }{4 \mu} z + \hat f(z,t), \quad g(z,t) ={-} \frac{{\mathcal{R}}^2 \hat f(z,t) }{z}, \end{equation}

where $p_H$ is a real constant and $\hat f(z,t)$ is analytic and single-valued in the fluid region $|z| > {\mathcal {R}}$ except for a simple pole at infinity, i.e.

(3.14)\begin{equation} \hat f(z,t) \sim \frac{\hat p(t) }{4 \mu} z + U_B(t) + { O }(1/z), \end{equation}

as $|z| \to \infty$ where $\hat p(t)$ is real-valued. The first term of $f(z,t)$ in (3.13) encodes the hydrostatic pressure $p_H$ of a clean bubble and the additional term $\hat f(z,t)$ will describe the quasi-steady Stokes flow generated by the surfactant effects. The quantity $\hat p(t)$ represents the modification to the far-field fluid pressure due to the presence of the surfactant and it is easy to check from (3.5) and (2.7) that the constant term in the far-field asymptotics (3.14) is the bubble speed $U_B(t)$. An important feature of the choice (3.13) is that it satisfies the streamline condition (2.3) on the bubble surface for any $\hat f(z,t)$. This is because, on $|z| = {\mathcal {R}}$,

(3.15)\begin{equation} \psi(z, \bar{z}, t) = {\rm Im}[\bar{z} f(z,t) + g(z,t)] = {\rm Im} \left [ \bar{z} \left (\frac{p_H }{4 \mu} z + \hat f(z,t) \right ) - \frac{{\mathcal{R}}^2 \hat f(z,t) }{z} \right ] = 0, \end{equation}

where the fact that $\bar {z}={\mathcal {R}}^2/z$ on the bubble boundary has been used. The bubble boundary is therefore a streamline.

On substitution of the decompositions (3.13) into the definition of $H(z, \bar {z}, t)$ given in (3.6) it follows that, on $|z|= {\mathcal {R}}$,

(3.16)\begin{align} H(z, \bar{z}, t) &= \frac{p_H }{4 \mu} z + \hat f(z,t) + \frac{p_H }{4 \mu} z + z \overline{\hat f'(z,t)} - {\mathcal{R}}^2 \overline{\left (\frac{\hat f'(z,t) }{z} \right )} + {\mathcal{R}}^2\overline{\left (\frac{\hat f(z,t) }{z^2}\right ) }\nonumber\\ &= \frac{p_H }{2 \mu} z + \hat f(z,t) +{\mathcal{R}}^2 \overline{\left (\frac{\hat f(z,t) }{z^2}\right ) }, \end{align}

where the fact that ${z} = {\mathcal {R}}^2/\bar {z}$ on $|z|= {\mathcal {R}}$ has been used. On division by $z$, this becomes

(3.17)\begin{equation} \frac{H(z, \bar{z},t) }{z} = \frac{p_H }{2\mu} + 2 {\rm Re} \left [ \frac{\hat f(z,t) }{z} \right ] = \frac{p_H }{2\mu} + {\rm Re}[h(z,t)], \end{equation}

where

(3.18)\begin{equation} h(z,t) \equiv \frac{2 \hat f(z,t) }{z}. \end{equation}

The function $h(z,t)$ is analytic and single-valued in the fluid region, properties it inherits from $\hat f(z,t)$ in view of its definition (3.18) and the far-field behaviour (3.14). Two expressions for $H/z$ have now been derived in (3.12) and (3.17). Setting them equal leads to

(3.19)\begin{equation} \frac{p_H }{2\mu} + {\rm Re}[h(z,t)] = \frac{\beta \varGamma }{2\mu {\mathcal{R}}} + \frac{1 }{2\mu} \left (p_B - \frac{\sigma_c }{{\mathcal{R}}} \right ). \end{equation}

It turns out that the boundary slip velocity $U(s,t)$ can also be conveniently expressed in terms of $h(z,t)$. To see this, note that on $|z|= {\mathcal {R}}$, where $\bar {z} = {\mathcal {R}}^2/{z}$, it follows from (3.5) and (3.13) that

(3.20)\begin{equation} u - {\rm i} v ={-}\overline{\hat f(z,t)} + \bar{z} \hat f'(z,t) - {\mathcal{R}}^2 \frac{\hat f'(z,t) }{z} + {\mathcal{R}}^2 \frac{\hat f(z,t) }{z^2} ={-}\overline{\hat f(z,t)} + {\mathcal{R}}^2 \frac{\hat f(z,t) }{z^2}. \end{equation}

Using the fact that if $a=a_x+\textrm {i} a_y$ and $b=b_x+\textrm {i}b_y$ are the complex analogues of the vectors $\boldsymbol {a}=(a_x, a_y)$ and $\boldsymbol {b}=(b_x, b_y)$ then the complex analogue of the dot product $\boldsymbol {a}\boldsymbol {\cdot }\boldsymbol {b}$ is $\textrm {Re}[a \bar {b}]$ then the boundary slip velocity $U(s,t)$ can be written, in complex form, as

(3.21)\begin{align} U(s,t) &= \boldsymbol{t}\boldsymbol{\cdot} \boldsymbol{u} = {\rm Re} \left [ - \frac{{\rm i} z }{{\mathcal{R}}} \left (-\overline{\hat f(z,t)} + {\mathcal{R}}^2 \frac{\hat f(z,t) }{z^2} \right ) \right ]\nonumber\\ &= {\rm Re} \left [ - {{\rm i} {\mathcal{R}}} \left (\frac{\hat f(z,t) }{z} - \overline{ \left (\frac{\hat f(z,t) }{z} \right )} \right ) \right ] = {\mathcal{R}} \,{\rm Im} \left [ \frac{\hat f(z,t) }{z} - \overline{ \left (\frac{\hat f(z,t) }{z} \right )} \right ], \end{align}

where the complex form of the unit tangent (3.8) has been used. Therefore, on the boundary,

(3.22)\begin{equation} \frac{U(s,t) }{{\mathcal{R}}} = 2 \,{\rm Im} \left [ \frac{\hat f(z,t) }{z} \right ] = {\rm Im}[h(z,t)]. \end{equation}

4. A complex partial differential equation of Burgers type

A velocity scale associated with the presence of the surfactant is

(4.1)\begin{equation} U_0 = \frac{\beta \langle \varGamma_0 \rangle }{2 \mu}. \end{equation}

It is natural to non-dimensionalize lengths using the bubble radius ${\mathcal {R}}$, surfactant concentrations using $\langle \varGamma _0 \rangle$, velocities induced by the presence of the surfactant using $U_0$ and time using ${\mathcal {R}}/U_0$. The hydrostatic pressure $p_H$ and bubble pressure $p_B$ are non-dimensionalized using $\sigma _c/{\mathcal {R}}$. The bubble boundary is now $|z|=1$ and it can be parametrized by $z=\textrm {e}^{-\textrm {i}s}$, where $s$ is the non-dimensional arclength. Noting that $\hat f(z,t)$ has the dimension of a velocity, the non-dimensional version of (3.22) is

(4.2)\begin{equation} {\tilde U(s,t)} = {\rm Im}[\tilde h(z,t)], \end{equation}

where a quantity decorated with a tilde denotes its non-dimensional counterpart. Equation (3.19) becomes

(4.3)\begin{equation} \frac{\sigma_c }{2 \mu {\mathcal{R}}} \tilde p_H + \frac{U_0 }{{\mathcal{R}}}\, {\rm Re}[\tilde h(z,t)] = \frac{\sigma_c }{2 \mu {\mathcal{R}}} (\tilde p_B-1) + \frac{\beta \langle \varGamma_0 \rangle }{2 \mu {\mathcal{R}}} \tilde \varGamma \end{equation}

or

(4.4)\begin{equation} \tilde p_H + \frac{2 \mu U_0 }{\sigma_c}\, {\rm Re}[\tilde h(z,t)] = \tilde p_B -1 + \frac{2 \mu U_0 }{\sigma_c} \tilde \varGamma, \end{equation}

if (4.1) is used. The capillary number, which was mentioned earlier, can now be introduced as

(4.5)\begin{equation} Ca=\frac{2 \mu U_0 }{\sigma_c} \end{equation}

and taken to be small, i.e. $Ca \ll 1$. In terms of it, (4.4) becomes

(4.6)\begin{equation} \tilde p_H + Ca\,{\rm Re}[\tilde h(z,t)] = \tilde p_B -1 +Ca\,\tilde \varGamma. \end{equation}

Hence, at leading order, the Laplace–Young balance holds:

(4.7)\begin{equation} \tilde p_B - \tilde p_H=1, \end{equation}

where the constant right-hand side encodes the constant curvature of the interface and, at first order in $Ca$, it follows from (4.6) that

(4.8)\begin{equation} {\rm Re}[\tilde h(z,t)] = \tilde \varGamma. \end{equation}

A consequence of (4.8) is that the average of the real part of $\tilde h(z,t)$ around the bubble boundary is unity since, by the choice of scaling, this is the value of the surface average of the non-dimensionalized surfactant concentration.

Henceforth, the tildes on any non-dimensionalized quantities will be dropped. Together, (4.2) and (4.8) imply that

(4.9)\begin{equation} h(z,t) = \varGamma(s,t) + {\rm i} U(s,t) \quad {\rm on}\ |z|=1. \end{equation}

Equation (4.9) is important: it is the radial geometry analogue of a similar relation obtained in Crowdy (2021b,c) for a half-plane geometry for which the boundary of the viscous fluid region is an infinite straight line. A subsequent trivial, but important, observation is that

(4.10)\begin{equation} h(z,t)^2 = \varGamma(s,t)^2 - U(s,t)^2 + 2 {\rm i} \varGamma(s,t) U(s,t) \quad {\rm on}\ |z|=1, \end{equation}

where (4.9) has simply been squared.

It is expedient now to return to the surfactant evolution equation (2.5) which, on use of (4.9) and (4.10), takes the non-dimensionalized form

(4.11)\begin{equation} {\rm Re} \left [ \frac{\partial h(z,t) }{\partial t} + \frac{\partial }{\partial s} \left (-\frac{{\rm i} h(z,t)^2 }{2} \right ) - \frac{1 }{Pe_s} \frac{\partial^2 h(z,t) }{\partial s^2} \right ] = 0 \quad {\rm on}\ |z|=1, \end{equation}

where the surface Péclet number is

(4.12)\begin{equation} Pe_s = \frac{U_0 {\mathcal{R}} }{D_s}. \end{equation}

By the chain rule, since $z=\textrm {e}^{-\textrm {i}s}$ on the bubble boundary,

(4.13)\begin{equation} \frac{\partial }{\partial s} = \frac{{\rm d} z }{{\rm d}s} \frac{\partial }{\partial z} ={-} {\rm i} z \frac{\partial }{\partial z}, \end{equation}

hence (4.11) can be written as

(4.14)\begin{equation} {\rm Re} \left [ \frac{\partial h(z,t) }{\partial t} - z h(z,t) \frac{\partial h(z,t) }{\partial z} + \frac{1 }{Pe_s} z \frac{\partial }{\partial z} \left ( z \frac{\partial h(z,t) }{\partial z} \right ) \right ] = 0. \end{equation}

The quantity in square brackets in (4.14) is analytic and single-valued in $|z| > 1$ except possibly at infinity. However, the problem under current consideration is such that

(4.15a,b)\begin{equation} h(z,t) \sim 1 + { O }(1/z), \quad h'(z,t) \sim { O }(1/z^2), \end{equation}

where the first term in the far-field behaviour of $h(z,t)$ ensures that the surface average of the real part of $h(z,t)$ is unity, a requirement just noted. This is because, being analytic and single-valued in $|z| > 1$, $h(z,t)$ has a convergent Laurent series there and only the constant term in this series will contribute to the average of $\textrm {Re}[h(z,t)]$ around the bubble boundary. The behaviour (4.15) means that the function in square brackets in (4.14) is analytic and single-valued for $|z| > 1$, including as $|z| \to \infty$ where it decays like $1/z$. Given that, according to (4.14), this function also has vanishing real part on $|z|=1$ it follows by analytic continuation off the boundary circle $|z|=1$ that

(4.16)\begin{equation} \frac{\partial h(z,t) }{\partial t} - z h(z,t) \frac{\partial h(z,t) }{\partial z} + \frac{1}{Pe_s} z \frac{\partial }{\partial z} \left ( z \frac{\partial h(z,t) }{\partial z} \right )= 0, \end{equation}

everywhere in $|z| > 1$.

Equation (4.16) is a key result of this paper. It is the radial geometry analogue of a complex Burgers equation obtained for the half-plane geometry in Crowdy (2021b,c) where, in that case, the relevant lower-analytic function $h(z,t)$ had a different functional connection to $f(z,t)$. The reduction of the swimming bubble problem to this complex partial differential equation of Burgers type (4.16) has significant theoretical ramifications to be explored next.

5. Bubble migration as $Pe_s \to \infty$: method of characteristics

The case of infinite surface Péclet number is studied first. On taking the limit $Pe_s \to \infty$, implying negligible surface diffusion, the governing equation (4.16) reduces to

(5.1)\begin{equation} \frac{\partial h(z,t) }{\partial t} - z h(z,t) \frac{\partial h(z,t) }{\partial z} = 0. \end{equation}

This can be solved by a complex method of characteristics in the spirit of similar calculations carried out for the half-plane geometry in Crowdy (2021b,c). Equation (5.1) implies that

(5.2a,b)\begin{equation} \frac{{\rm d} h }{{\rm d}t} = 0 \quad {\rm or} \quad h(z,t) = H(Z) \end{equation}

on complex characteristics defined by

(5.3)\begin{equation} \frac{{\rm d}z }{{\rm d}t} ={-}z h(z,t) \quad {\rm with}\ z=Z\ {\rm at}\ t=0. \end{equation}

The variable $Z$ can be thought of as labelling the characteristics; the function $H(Z)$ is determined by initial conditions: $h(z,0)=h(Z,0) = H(Z)$. Equations (5.2) and (5.3) together imply that

(5.4)\begin{equation} \frac{{\rm d}z }{{\rm d}t} ={-}z H(Z) \quad {\rm with}\ z=Z\ {\rm at}\ t=0 \end{equation}

implying

(5.5a,b)\begin{equation} \frac{{\rm d} \log z }{{\rm d}t} ={-} H(Z) \quad {\rm or} \quad z = Z \,{\rm e}^{{-}H(Z)t} \end{equation}

after an integration is performed and initial conditions imposed. An implicit form of the general solution to the problem, parametrized by the complex variable $Z$, is therefore

(5.6)\begin{equation} h(z,t) = H(Z), \quad z = Z \,{\rm e}^{{-}H(Z)t}. \end{equation}

For a given $H(Z)$ formulas (5.6) give an implicit parametric representation of the solution for arbitrary initial data from which the time-evolving solution can easily be extracted numerically by a nonlinear solver. The swimming bubble problem at infinite surface Péclet number is therefore integrable in this sense.

The next subsection showcases a particular class of initial conditions for which this implicit solution (5.6) can be rendered explicit in terms of the Lambert W-function (Olver et al. 2020).

5.1. A special class of initial conditions

Suppose that

(5.7)\begin{equation} H(Z) = 1 + \frac{B }{Z}, \quad |B| \le 1, \end{equation}

where $B$ is a real constant. It follows that, on the bubble surface,

(5.8)\begin{equation} h({\rm e}^{-{\rm i} s},0) = 1 + B \,{\rm e}^{{\rm i} s} = 1 + B \cos s + {\rm i} B \sin s = \varGamma(s,0)+ {\rm i} U(s,0) \end{equation}

so the corresponding initial surfactant distribution can be read off as

(5.9)\begin{equation} \varGamma_0(s) = 1 + B \cos s. \end{equation}

This is non-negative everywhere on the bubble boundary because of the stipulation that $|B| \le 1$. If $0 < B \le 1$ the maximum value $1+B$ of the surfactant concentration is at the front of the bubble where $z=1$, the minimum value $1-B$ is at the rear of the bubble. In this case, according to (2.1), the surface tension at the front of the bubble is less than that at its rear and the bubble is expected to move to the right with some speed $U_B(t)$ to be determined next. Being an even function of $s$, this initial surfactant concentration (5.9) is symmetric about the axis through the bubble centre, as required.

With the choice (5.7) it follows from the general solution (5.6) that

(5.10)\begin{equation} h(z,t) = H(Z) = 1 + \frac{B }{Z} \quad {\rm with\ } \ z = Z\, {\rm e}^{{-}t - Bt/Z} \end{equation}

or, on rearrangement of the second equation,

(5.11)\begin{equation} \frac{z\,{\rm e}^{t} }{Z} \,{\rm e}^{{Bt}/{Z}} = \left (\frac{z \,{\rm e}^{t} }{Bt} \right ) \left (\frac{B t }{Z} \right ) {\rm e}^{{Bt}/{Z}} = 1. \end{equation}

For any given $t$ and $z$, the equation

(5.12)\begin{equation} {\mathcal{Z}}\, {\rm e}^{\mathcal{Z}} = \frac{Bt \,{\rm e}^{{-}t} }{z} \end{equation}

must be solved for the unknown variable ${\mathcal {Z}} \equiv Bt/Z$. Therefore,

(5.13)\begin{equation} {\mathcal{Z}} = \frac{B t }{Z} = {\rm W} \left(\frac{Bt \,{\rm e}^{{-}t}}{z}\right), \end{equation}

where $\textrm {W}$ is the (zero branch of the) Lambert W-function (Olver et al. 2020). The analytic functions $f(z,t)$ and $g(z,t)$ associated with the quasi-steady Stokes flow generated around the bubble by the spreading surfactant can then be given explicitly in terms of this special function. Indeed,

(5.14a,b) \begin{equation} h(z,t) = \frac{2 \hat f(z,t) }{z} = H(Z) = 1+ \frac{1 }{t} {\rm W} \left (\frac{Bt \,{\rm e}^{{-}t}}{z}\right ), \qquad g(z,t) ={-} \frac{\hat f(z,t)}{z}. \end{equation}

On substitution into (3.4) the streamfunction for the flow is

(5.15)\begin{equation} \psi(z, \bar{z}, t) = {\rm Im} \left [ \frac{1 }{2} (z \bar{z} - 1) \left (1+ \frac{1 }{t} {\rm W} \left (\frac{Bt \,{\rm e}^{{-}t}} {z} \right ) \right ) \right ]. \end{equation}

Furthermore, on setting $z= \textrm {e}^{-\textrm {i} s}$ the surfactant concentration and slip velocity are given as explicit functions of $s$ and $t$ by

(5.16a,b)\begin{equation} \varGamma(s,t) = {\rm Re} \left [1+ \frac{1}{t} {\rm W} \left (\frac{Bt \,{\rm e}^{{-}t}} {{\rm e}^{-{\rm i} s}} \right ) \right ], \quad U(s,t) = {\rm Im} \left [ \frac{1 }{t} {\rm W} \left (\frac{Bt \,{\rm e}^{{-}t}} {{\rm e}^{-{\rm i} s}} \right ) \right ]. \end{equation}

Figure 3 shows the evolution of the surfactant concentration $\varGamma (s,t)$ and slip velocity $U(s,t)$ for $Pe_s=\infty$ over the bubble boundary for $B=0.9$ in the initial condition (5.7) as computed from (5.16). The graphs show that as the surfactant spreads over the surface the Marangoni-stress-induced surface slip dies away until, at large times, it vanishes and the bubble motion is arrested.

Figure 3. Evolution of (a) the surfactant concentration $\varGamma (s,t)$ and (b) slip velocity $U(s,t)$ for $Pe_s=\infty$ over the bubble boundary for $B=0.9$ in the initial condition (5.7) as computed from (5.16). As the surfactant spreads over the surface the Marangoni-stress-induced surface slip dies away.

The bubble velocity $U_B(t)$ can be extracted as follows. Suppose that

(5.17)\begin{equation} h(z,t) = \frac{2 \hat f(z,t) }{z} \sim 1 + \frac{h_1(t) }{z} + { O }(1/z^2) \quad {\rm as}\ z \to \infty. \end{equation}

Hence, using the non-dimensional versions of (3.5), (3.13) and (3.20):

(5.18)\begin{equation} u - {\rm i} v ={-}\overline{\hat f(z,t)} + \bar{z} \hat f'(z,t) - \frac{\hat f'(z,t) }{z} + \frac{\hat f(z,t) }{z^2} \sim{-}\frac{\overline{h_1(t)} }{2} + { O }(1/z), \end{equation}

which, by (2.7), leads to the identification

(5.19)\begin{equation} U_B(t) = \frac{\overline{h_1(t)} }{2}. \end{equation}

But since

(5.20)\begin{equation} h(z,t) =1 + \frac{B }{Z} \quad {\rm with} \ z = Z \,{\rm e}^{{-}t - {Bt}/{Z}}, \end{equation}

then for large $z$,

(5.21)\begin{equation} \frac{1}{Z} \sim \frac{{\rm e}^{{-}t } }{z} + { O }(1/z^2) \end{equation}

and hence

(5.22)\begin{equation} h(z,t) =1 + \frac{B }{Z} \sim 1 + \frac{B\, {\rm e}^{{-}t } }{z}+ { O }(1/z^2), \end{equation}

from which it follows, on comparing with (5.17), that $h_1(t) = B \,\textrm {e}^{-t}$. From (5.19), the bubble velocity is therefore

(5.23)\begin{equation} U_B(t) = \frac{B \,{\rm e}^{{-}t } }{2}. \end{equation}

The total bubble displacement $\Delta x$ due to the spreading of surfactant is

(5.24)\begin{equation} \Delta x = \int_0^\infty U_B(t)\,{\rm d}t = \int_0^\infty \frac{B \,{\rm e}^{{-}t } }{2} \,{\rm d}t = \frac{B }{2}. \end{equation}

Consequently, after the surface activity illustrated in the graphs of figure 3 and any further activity as $t \to \infty$, the bubble will have displaced to the right by a distance $B/2 = 0.45$.

5.2. Formation of a weak singularity at finite time

The case $B=1$ is of special interest because, for this initial condition, the rear of the bubble is initially clean, i.e. $\varGamma _0(\pm {\rm \pi})=0$, as is evident from (5.9). This turns out to have interesting consequences. Crowdy (2021b) has studied a similar circumstance of an isolated clean point existing in the initial surfactant distribution on the infinite free surface bounding a half-plane fluid layer and identified the formation of a weak singularity at finite time, $t_*$ say. During the ‘waiting time’ $0 \le t < t_*$, before the singularity formation, the isolated clean point remains clean. At $t=t_*$ there is an instantaneous blow-up of the first derivatives $\partial \varGamma (s,t)/\partial s$ and $\partial U(s,t)/\partial s$ at the clean point, but these do not lead to termination of the solution. Rather, the singularity is glancing and both $\partial \varGamma (s,t)/\partial s$ and $\partial U(s,t)/\partial s$ return to finite values for $t > t_*$ with the clean point now being contaminated with surfactant. Since the discovery of this weak singularity in Crowdy (2021b), other authors have investigated similar phenomena in other circumstances but still in the semi-infinite fluid-layer geometry (Bickel & Detcheverry 2022; Temprano-Coleto & Stone 2024).

The formation of an analogous weak singularity also occurs in the bubble geometry for the initial condition (5.7) when $B=1$ as is now shown. By the symmetry of this initial condition about the $x$ axis the slip velocity at the rear of the bubble is necessarily zero at all times, i.e. $U(\pm {\rm \pi},t)=0$, but let the surfactant concentration there be denoted by $\varGamma _r(t)$, i.e.

(5.25)\begin{equation} \varGamma_r(t) \equiv \varGamma({\pm} {\rm \pi}, t). \end{equation}

It follows from (4.9) that

(5.26)\begin{equation} h({-}1,t) = \varGamma_r(t). \end{equation}

Crowdy (2021b) showed the existence of a finite-time weak singularity associated with an isolated clean point on the boundary of a half-plane fluid region by considering the dynamics of square-root branch-point singularities of (the relevant) $h(z,t)$ in the unphysical region of the complex plane. He showed that such a square-root branch-point reached the physical boundary in finite time (indeed, at the singularity formation time) but did not cause termination of the solution by entering the fluid region (where it is not allowed) but immediately turned around and re-entered the unphysical region of the complex plane thereby allowing a smooth continuation in time of the solution. For the bubble geometry, it is more convenient to demonstrate the weak singularity formation by returning to the implicit form of the solution given by (5.10) with $B=1$. It follows that

(5.27)\begin{equation} h({-}1,t)= H(Z) = 1 + \frac{1 }{Z} = \varGamma_r(t) \quad {\rm with}\ {-}1 = Z \,{\rm e}^{{-}t(1+1/Z)}. \end{equation}

Hence,

(5.28)\begin{equation} \varGamma_r(t) = 1 + \frac{1 }{Z} = 1 - {\rm e}^{{-}t(1+1/Z)} = 1 - {\rm e}^{{-}t \varGamma_r(t)}, \end{equation}

which constitutes a nonlinear equation determining $\varGamma _r(t)$. A trivial solution is $\varGamma _r(t)=0$ which corresponds to the rear of the bubble being clean. However, to explore the possibility of other solutions to this nonlinear equation for $\varGamma _r(t)$ it is useful to plot, as functions of $\varGamma _r \ge 0$, graphs of the two functions

(5.29a,b)\begin{equation} y= \varGamma_r, \quad y = 1 - {\rm e}^{{-}t \varGamma_r} \end{equation}

and viewing $t$ as a parameter. This is done in figure 4 where the graph $y=\varGamma _r$, shown in black, is independent of $t$ and four instances of the graph $y = 1 - \textrm {e}^{-t \varGamma _r}$, for $t=0.5$, 1, 1.5, 2 are shown in blue. According to (5.28) solutions for $\varGamma _r(t)$ occur where any blue graph intersects the black graph. The gradient ${\textrm {d}\kern 0.05em y}/\textrm {d}\varGamma _r$ of any graph of $y = 1 - \textrm {e}^{-t \varGamma _r}$ is monotonic decreasing with its maximum value occurring at $\varGamma _r=0$. It is easy to see that $t=t_* = 1$ represents the critical case where the gradient of $y = 1 - \textrm {e}^{-t \varGamma _r}$ at $\varGamma _r=0$ is unity, the same as the gradient of the black curve $y=\varGamma _r$ there. For $t > t_*=1$ the blue curves have a larger gradient than the black curve at $\varGamma _r=0$ and it is clear geometrically from figure 4 that all blue graphs then curve down and have a single intersection point with the black curve at some value of $\varGamma _r > 0$: the value of $\varGamma _r=\varGamma _r(t)$ at this intersection point for $t > t_*$ is the surfactant concentration at the rear of the bubble after the weak singularity has occurred at $t=t_*=1$. It is easy to show using local expansions that, just after the singularity formation time, a good leading-order approximation of $\varGamma _r(t)$ is furnished by

(5.30)\begin{equation} \varGamma_r(t) \approx \frac{2 (t-1) }{t^2} \quad 0 \le t-1 \ll 1. \end{equation}

Figure 5 features graphs of $\varGamma (s,t)$ and $U(s,t)$ as functions of $s$, as computed from (5.16), both before and after $t=t_*=1$. These clearly show the instantaneous blow-up, and subsequent resolution, of the first derivatives $\partial \varGamma (\pm {\rm \pi},1)/\partial s$ and $\partial U(\pm {\rm \pi},1)/\partial s$ at the rear of the bubble at $t=t_*=1$.

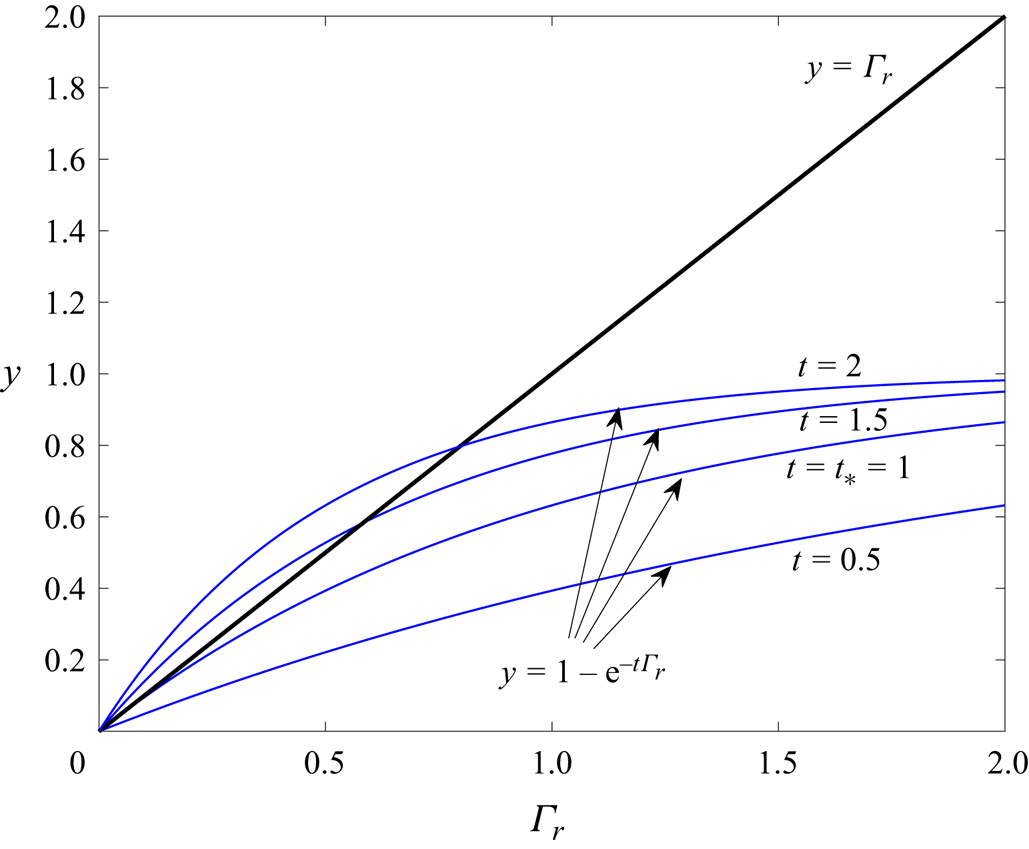
Figure 4. The two graphs (5.29) for different values of the parameter $t$. Admissible solutions for $\varGamma _r(t)$ correspond to intersections of any blue graph of $y = 1 - \textrm {e}^{-t \varGamma _r}$ with the black graph $y=\varGamma _r$. From the geometry of these graphs the clean-point solution $\varGamma _r=0$ is the only admissible solution until $t > t_*=1$ when contamination of the rear of the bubble occurs.

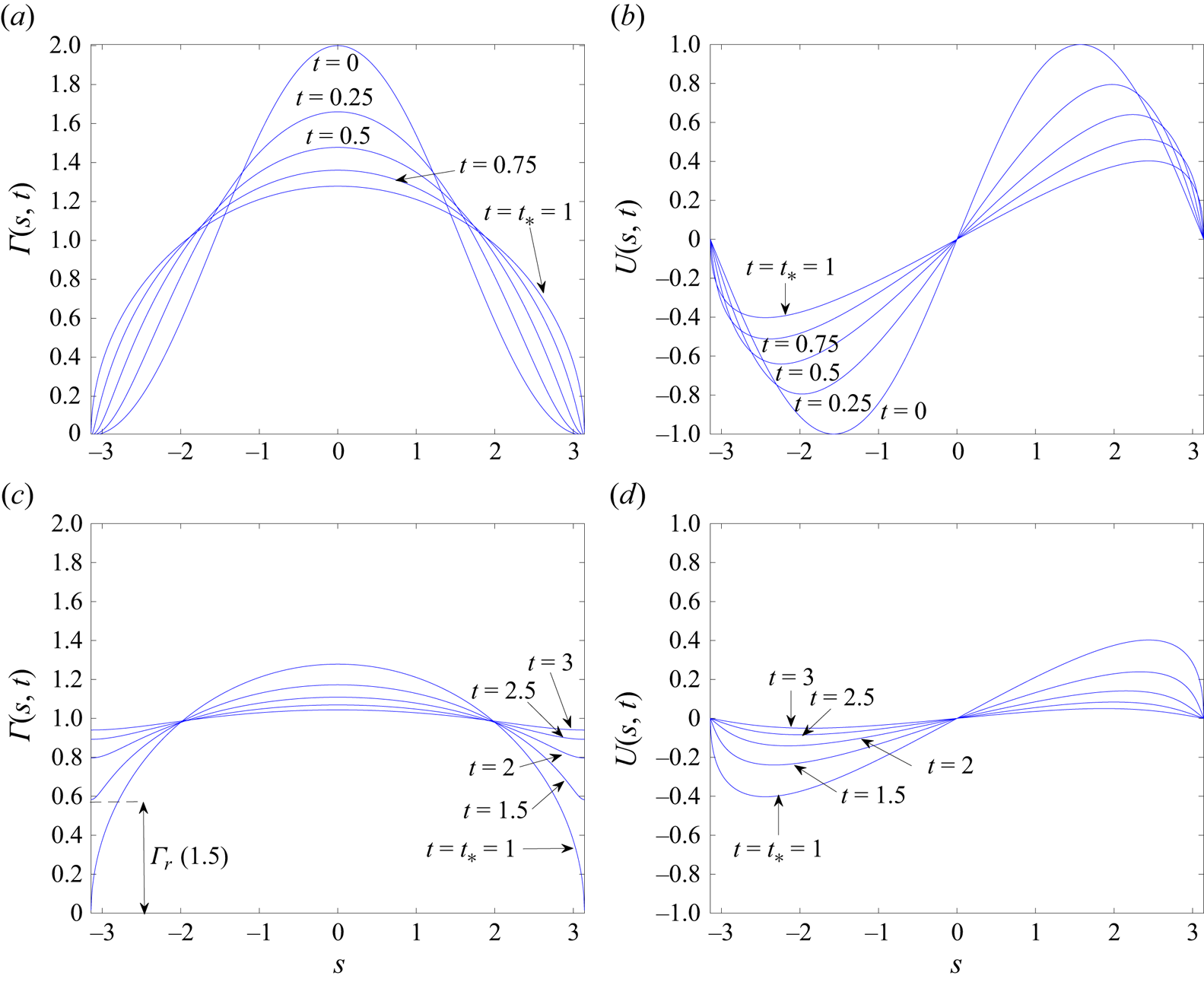
Figure 5. Formation of a weak singularity due to an isolated clean point at the rear of the bubble (at $s = \pm {\rm \pi}$) when $B=1$ in the initial condition (5.7). Plots of (a) $\varGamma (s,t)$ and (b) $U(s,t)$ as a function of $s$ at $Pe_s=\infty$ for $t=0$, 0.25, 0.5, 0.75 and $t=t_*=1$ where the weak singularity occurs. The rear of the bubble remains clean, i.e. $\varGamma _r =0$, throughout the interval $0 \le t \le t_*$. (c,d) The continuation past the singularity for $t=t_*=1$, 1.5, 2, 2.5 and $t=3$ where the rear of the bubble has become contaminated, i.e. $\varGamma _r > 0$ for $t > t_*=1$.

This weak singularity formation in the surface variables does not affect any of the earlier deductions about the bubble speed $U_B(t)$ or net displacement $\Delta x$. Therefore, after the surface activity illustrated in figure 5 and any further activity as $t \to \infty$, this bubble will have displaced to the right by a distance $\Delta x = B/2 = 0.5$ in accordance with (5.24).

6. Bubble migration for $0 < Pe_s < \infty$: a Cole–Hopf-type linearization

While the method of characteristics provides an implicit parametric representation of the general solution when $Pe_s$ is infinite, for $0 < Pe_s < \infty$ the nonlinear problem turns out to be linearizable by a complex variant of the classical Cole–Hopf transformation (Whitham 1999). To see this, it is useful to view $h(z,t)$ as a function of a new independent variable ${\mathcal {Z}}$ as follows:

(6.1)\begin{equation} {\mathcal{H}}({\mathcal{Z}},t) = h(z,t) \quad {\mathcal{Z}} = \log z. \end{equation}

Since $z {\partial /\partial z} = \partial /\partial {\mathcal {Z}}$ then (4.16) becomes

(6.2)\begin{equation} -\frac{\partial {\mathcal{H}}({\mathcal{Z}},t) }{\partial t} + {\mathcal{H}}({\mathcal{Z}},t)\frac{\partial {\mathcal{H}}({\mathcal{Z}},t) }{\partial {\mathcal{Z}}} = \frac{1 }{Pe_s} \frac{\partial^2 {\mathcal{H}}({\mathcal{Z}},t) }{\partial {\mathcal{Z}}^2}, \end{equation}

which differs from a standard complex Burgers equation for ${\mathcal {H}}({\mathcal {Z}},t)$ only in the sign of the first term. Assuming the principal branch of the complex logarithm the domain of analyticity of ${\mathcal {H}}({\mathcal {Z}},t)$ is now the right semi-strip $\textrm {Re}[{\mathcal {Z}}] \ge 0, -{\rm \pi} < \textrm {Im}[{\mathcal {Z}}] \le {\rm \pi}$ in the complex ${\mathcal {Z}}$ plane and admissible solutions must be $2 {\rm \pi}\textrm {i}$-periodic as functions of ${\mathcal {Z}}$ in order that $h(z,t)$ is a single-valued function in the fluid. A subsequent change of dependent variable embodied in

(6.3)\begin{equation} {\mathcal{H}}({\mathcal{Z}},t) = 1 -\frac{2 }{Pe_s} \frac{\partial \log \varPhi({\mathcal{Z}},t) }{\partial {\mathcal{Z}}}, \end{equation}

where the second term on the right-hand side is assumed to decay as $z \to \infty$, turns (6.2) into

(6.4)\begin{equation} -\frac{\partial \varPhi({\mathcal{Z}},t) }{\partial t} + \frac{\partial \varPhi({\mathcal{Z}},t) }{\partial {\mathcal{Z}}}= \frac{1 }{Pe_s} \frac{\partial^2 \varPhi({\mathcal{Z}},t) }{\partial {\mathcal{Z}}^2} \end{equation}

after an integration with respect to ${\mathcal {Z}}$ and where an additive function of time has been set equal to zero. The latter choice is made without loss of generality in the sense that any other choice simply rescales $\varPhi ({\mathcal {Z}},t)$ by a function of time which has no effect on the logarithmic ${\mathcal {Z}}$-derivative determining ${\mathcal {H}}({\mathcal {Z}},t)$ in (6.3) and, as such, does not affect the physical flow.

Equation (6.3) is a complex variant of the classical Cole–Hopf transformation (Whitham 1999) differing from it not only because it involves complex-valued functions and variables, but also in the appearance of the first unity term in (6.3). This results in the modified form (6.4) of the classical heat equation; the latter equation is the linear partial differential equation arising after carrying out a standard Cole–Hopf transformation on the real Burgers equation. The important observation is that, even if it is not the usual heat equation, (6.4) is still nevertheless a linear partial differential equation, albeit a complex-valued one.

In view of its linear character it is natural to seek separable solutions of (6.4) having the form

(6.5)\begin{equation} \varPhi({\mathcal{Z}},t) = \sum_{n \ge 0} A_n(t) \,{\rm e}^{{-}n{\mathcal{Z}}}, \end{equation}

this being a general representation of a $2 {\rm \pi}\textrm {i}$-periodic function that is analytic in the right semi-strip and decaying as $\textrm {Re}[{\mathcal {Z}}] \to \infty$. These properties are necessary to ensure that ${\mathcal {H}}({\mathcal {Z}},t)$ as given by (6.3) gives rise, according to (6.1), to a function $h(z,t)$ with the required properties. Substitution of (6.5) into (6.4) leads to the linear system

(6.6)\begin{equation} \frac{{\rm d} A_n }{{\rm d}t} ={-} n \left (1 + \frac{n }{Pe_s} \right ) A_n \quad n \ge 0. \end{equation}

The solutions of these ordinary differential equations are

(6.7)\begin{equation} A_n(t) = A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t} \quad n \ge 0, \end{equation}

where the data $\{ A_{n0} = A_n(0) | n \ge 0 \}$ are determined by initial conditions. The solution for $\varPhi ({\mathcal {Z}},t)$ follows as

(6.8)\begin{equation} \varPhi({\mathcal{Z}},t) = \sum_{n \ge 0} A_{n0}\, {\rm e}^{{-}n(n+1/Pe_s)t} \,{\rm e}^{{-}n{\mathcal{Z}}} \end{equation}

giving

(6.9)\begin{equation} {\mathcal{H}}({\mathcal{Z}},t) = 1 + \frac{2 }{Pe_s} \frac{\displaystyle\sum_{n \ge 1} n A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t} \,{\rm e}^{{-}n{\mathcal{Z}}} }{\displaystyle\sum_{n \ge 0} A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t} \,{\rm e}^{{-}n{\mathcal{Z}}}} \end{equation}

or, on back substitution into (6.3) and from (6.1),

(6.10)\begin{equation} h(z,t) = 1 + \frac{2 }{Pe_s} \frac{\displaystyle\sum_{n \ge 1} n A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t}/z^n }{\displaystyle\sum_{n \ge 0} A_{n0} \,{\rm e}^{{-}n(n+1/Pe_s)t}/z^n }. \end{equation}

This is an explicit solution for arbitrary initial data and for any finite non-zero value of $Pe_s$.

Consider now the initial conditions (5.7) for which the $Pe_s=\infty$ solution has been found in § 5.1 in terms of Lambert-W functions. It is of interest to examine how surface diffusion affects this solution. For this it is necessary to pick

(6.11)\begin{equation} -\frac{2 }{Pe_s} \frac{\partial \log \varPhi({\mathcal{Z}},0) }{\partial {\mathcal{Z}}} = B \,{\rm e}^{-{\mathcal{Z}}} \quad {\rm or} \quad \varPhi({\mathcal{Z}},0) = {\rm e}^{Pe_s B \,{\rm e}^{-{\mathcal{Z}}}/2}, \end{equation}

from which it follows that

(6.12)\begin{equation} A_{n0} = \left ( \frac{Pe_s B }{2} \right )^n \frac{1 }{n!} \quad n \ge 0. \end{equation}

Substitution of these coefficients into (6.10) gives the solution for $h(z,t)$. The speed of the bubble $U_B(t)$ follows from the large-$z$ asymptotics of (6.10). As $z \to \infty$,

(6.13)\begin{equation} h(z,t) \sim 1 + \frac{2 }{Pe_s} \frac{A_{10} \,{\rm e}^{-(1+1/Pe_s)t} }{z} + { O }(1/z^2) \end{equation}

so that, from (5.19),

(6.14)\begin{equation} U_B(t) = \frac{1 }{Pe_s} A_{10}\,{\rm e}^{-(1+1/Pe_s)t} = \frac{B }{2} \,{\rm e}^{-(1+1/Pe_s)t} \end{equation}

and

(6.15)\begin{equation} \Delta x = \int_{0}^\infty \frac{B }{2} \,{\rm e}^{-(1+1/Pe_s)t'} \,{\rm d}t' = \frac{B }{2 (1+1/Pe_s)}. \end{equation}

As $Pe_s \to \infty$, the results (6.14) and (6.15) tend, respectively, to (5.23) and (5.24), as expected. On comparing (5.23) and (6.14) surface diffusion is seen to slow down the bubble and, on comparing (5.24) and (6.15), to reduce its total displacement.

Figure 6 compares the evolution of the surfactant concentration $\varGamma (s,t)$ at finite $Pe_s=10$ and $1$ with the analogous evolution in the case of infinite $Pe_s$ for the initial condition (5.7) with $B=0.5$. In the absence of any additional forcing, surface diffusion aids in more quickly mollifying any surfactant concentration gradients and effectively enhances the rate of surfactant spreading to the uniform coverage state. As a result, the overall displacement of the bubble lessens with enhanced surface diffusion, i.e. as $Pe_s$ decreases, a feature that is apparent from formula (6.15). The total bubble displacements after the surface activity shown in figure 6 for $Pe_s=\infty$, $10$ and $1$ are $0.2500$, $0.2273$ and $0.1250$, respectively.

Figure 6. The effect of surface diffusion. The graphs compare the evolution of the surfactant concentration $\varGamma (s,t)$ for $Pe_s=10$ and $\infty$ (a) and for $Pe_s=1$ and $\infty$ (b) for the initial condition (5.7) with $B=0.5$. The concentrations for $Pe_s=\infty$ are shown as solid blue lines, the finite-$Pe_s$ results as dashed red lines.

It is worth pointing out that, by a further simple change of variables, the governing equation (6.4) can be transformed to the backwards complex heat equation. At first sight, this may cause concern given the ill-posedness of many problems involving the real-valued backwards heat equation. However, in this case, as has been seen by explicit construction of the solution, this complex version is solved within a class of complex-valued analytic functions for which the evolution problem is well posed.

7. General initial surfactant distributions

The special initial condition (5.9) corresponds to a distribution with a well-defined excess of surfactant at the front of the bubble that falls off, symmetrically with respect to the $x$ axis, towards its rear. Can anything be said if the initial surfactant distribution has a more variegated profile, perhaps with a series of humps and troughs, though still symmetric with respect to the real axis?

For the case of infinite surface Péclet number the implicit general solution (5.6) encodes the dynamics, and it is easy to use this as a basis for a numerical computation of the solution, but it is not generally possible to make this solution explicit as done for the special initial condition considered in § 5.1. Nevertheless, quantitative statements about the velocity $U_B(t)$ and total displacement $\Delta x$ for more general initial surfactant distributions can still be made. For a more general, sufficiently smooth, initial surfactant distribution $\varGamma (s,0)= \varGamma _0(s)$ that is symmetric about the $x$ axis the associated $H(Z)$ will have, on $|Z|=1$, a convergent Laurent series of the form

(7.1)\begin{equation} H(Z) = 1 + \frac{B_1 }{Z} + \frac{B_2 }{Z^2} + \frac{B_3 }{Z^3} + \cdots. \end{equation}

By the assumed symmetry about the real axis, all the series coefficients $\{ B_n | n=1,2, \ldots \}$ will be real so that, on taking the real part of (7.1) to find the initial surfactant concentration it will have a Fourier cosine expansion in $s$. In particular,

(7.2)\begin{equation} B_1 = \frac{1 }{\rm \pi} \int_{-{\rm \pi}}^{\rm \pi} \varGamma_0(s) \cos s \,{\rm d} s. \end{equation}

It is straightforward to show, by extending the far-field asymptotics of § 5, that the speed of the bubble $U_B(t)$ and total displacement $\Delta x$ are

(7.3a,b)\begin{equation} U_B(t) = \frac{B_1 \,{\rm e}^{{-}t} }{2}, \quad \Delta x = \frac{B_1 }{2}, \end{equation}

which constitutes a quite general result. In summary, and returning now to dimensional variables, at infinite surface Péclet number, for any initial surfactant concentration $\varGamma _0(s)$, symmetric about the $x$ axis, the bubble velocity and its total displacement in the $x$ direction are given by

(7.4)\begin{equation} \left.\begin{array}{@{}c@{}} \displaystyle U_B(t) = \dfrac{\beta }{4 {\rm \pi}\mu {\mathcal{R}} } \left\{ \int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}} \varGamma_0(s) \cos \left (\dfrac{s }{{\mathcal{R}}} \right ) {\rm d} s \right \} \exp \left ( - \dfrac{\beta \langle \varGamma_0 \rangle t }{2 \mu {\mathcal{R}}} \right ), \\ \displaystyle \Delta x = \dfrac{1 }{2 {\rm \pi}\langle \varGamma_0 \rangle} \left\{ \int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}} \varGamma_0(s) \cos \left (\dfrac{s }{{\mathcal{R}}} \right ) {\rm d} s \right \}, \end{array}\right\} \end{equation}

where $\langle \varGamma _0 \rangle$ is the average surfactant concentration.

Similarly, a straightforward generalization to arbitrary initial conditions of the calculation given in § 6 for $0 < Pe_s < \infty$ leads to

(7.5) \begin{equation} \left.\begin{array}{@{}c@{}} \displaystyle U_B(t) = \dfrac{\beta }{4 {\rm \pi}\mu {\mathcal{R}} } \left\{ \int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}} \varGamma_0(s) \cos \left (\dfrac{s}{{\mathcal{R}}} \right ) {\rm d} s \right \} \exp \left ( - \dfrac{\beta \langle \varGamma_0 \rangle (1+1/Pe_s) t }{2 \mu {\mathcal{R}}} \right ), \\ \displaystyle \Delta x = \dfrac{1 }{2 {\rm \pi}\langle \varGamma_0 \rangle(1+1/Pe_s)} \left\{ \int_{-{\rm \pi} {\mathcal{R}}}^{{\rm \pi} {\mathcal{R}}} \varGamma_0(s) \cos \left (\dfrac{s }{{\mathcal{R}}} \right ) {\rm d} s \right \}. \end{array}\right\} \end{equation}

Formulas (7.5) reduce to formulas (7.4) as $Pe_s \to \infty$, as expected.

It is interesting that the net displacement depends only on the first two coefficients in a Fourier cosine series of the initial surfactant concentration: the coefficient $B_1$ is the second term in a Fourier cosine series of the initial surfactant concentration, the first term being the average surfactant concentration over the surface. The net bubble displacement is proportional to the ratio of these first two Fourier cosine coefficients with the constant of proportionality being a simple function of the surface Péclet number. Similar observations on the importance of a small number of early coefficients in the relevant series expansions determining the overall behaviour have been made in other problems of low-Reynolds-number locomotion driven by different surface actuation mechanisms (Crowdy 2013).

8. From inviscid bubbles to viscous droplets

The analysis of this paper generalizes easily to the two-fluid scenario where the inviscid bubble is replaced by a droplet of viscous fluid of different viscosity. The key steps are the same as for the two-fluid generalization carried out by Crowdy, Curran & Papageorgiou (2023) of the earlier single-fluid analysis of Crowdy (2021b,c) in the half-plane fluid geometry so they will only be sketched out here.

Suppose the outer fluid viscosity, which has been denoted throughout this paper by $\mu$, is now called $\mu _+$ with the generally different viscosity of the droplet fluid in $|z| <1$ denoted by $\mu _-$. It is natural to define corresponding Goursat functions $\hat f_\pm (z,t)$ and $g_\pm (z,t)$ in the two viscous fluid regions, and two corresponding functions

(8.1)\begin{equation} h_{{\pm}}(z,t) = \frac{2 \hat f_\pm(z,t) }{z}. \end{equation}

As done earlier, the functional relationships

(8.2)\begin{equation} g_{{\pm}}(z,t) ={-} \frac{{\mathcal{R}}^2 \hat f_\pm(z,t) }{z} \end{equation}

are imposed. The requirement that the tangential fluid velocities at the boundary of the droplet where the two fluids meet must be continuous turns out to furnish the following functional relationship:

(8.3)\begin{equation} h_+(z,t) ={-} \overline{h_-}({\mathcal{R}}^2/z,t), \end{equation}

where $\overline{q}(z,t)\equiv \overline {q(\bar {z},t)}$ denotes the usual Schwarz conjugate of an analytic function $q(z,t)$. The relation (8.3) means that there is a reflectional symmetry between the inner and outer Stokes flow solutions in this circular geometry. A similar observation was made by Crowdy et al. (2023) for the two fluids in neighbouring half-planes meeting at the flat interface between them. At small capillary number, there is still a leading-order Laplace–Young balance of normal fluid stresses on the boundary while the tangential stress condition now involves boundary tractions from both fluids balancing the Marangoni stress due to the surfactant. Ultimately, the principal modification to the analysis here is to replace $\mu$ by $(\mu _++\mu _-)$ and replace the characteristic velocity scaling $U_0$ given in (4.1) by

(8.4) \begin{equation} U_0 = \frac{\beta \langle \varGamma_0 \rangle }{2 (\mu_++\mu_-)}. \end{equation}

This clearly reduces to (4.1) when $\mu _-=0$.

9. Discussion

A simple model of viscous Marangoni migration of a two-dimensional bubble by surfactant spreading has been proposed and shown to be exactly solvable mathematically at all non-zero values of the surface Péclet number, including when surface diffusion is completely absent, or $Pe_s=\infty$. The work can be viewed as complementing a body of theoretical work on viscous Marangoni propulsion in the diffusion-dominated regime when the surface Péclet number vanishes and the problem becomes intrinsically linear (Lauga & Davis 2011; Crowdy 2020, 2021a). Surprisingly, as has been shown here, if surface advection is included the now apparently nonlinear problem can, in fact, also be linearized. While the formulation is valid for any $Pe_s > 0$ note that since both the Reynolds number and capillary number depend on the size of $U_0$, care must be taken to ensure the theory herein is only applied in circumstances where this velocity is such that the assumptions of low Reynolds and capillary numbers can safely be made.

The results here rely on a complex variable formulation of the Stokes flow problem characterized by a coupled analytical description of the surfactant and flow dynamics in terms of a single-valued analytic function $h(z,t)$ that is shown to satisfy a complex partial differential equation of Burgers type. At finite non-zero surface Péclet number, this reformulation is combined with further changes of variable generalizing the classical Cole–Hopf transformation revealing that this nonlinear problem is linearizable at any finite non-zero surface Péclet number. The governing linear complex partial differential equation is (6.4). This linearization is expected to have significant theoretical and numerical ramifications beyond those already set out here. Useful general formulas (7.4) and (7.5) show precisely how details of the initial surfactant distribution govern the bubble speed and its net displacement after long times. It is reasonable to conjecture that similar formulas might hold for a three-dimensional spherical bubble although that suggestion requires further investigation since none of the mathematical techniques used here carry over to that case.

In addition to characterizing the migration properties of the bubble due to surfactant spreading, the surface activity has also been fully resolved. Of particular note is the formation of a weak singularity: it is the analogue of a similar singularity first observed by Crowdy (2021b) in the half-plane fluid geometry and is associated with an isolated clean point on the free surface. Up to a well-defined finite (‘waiting’) time $t_*$ this clean point remains free of surfactant but, at $t=t_*$, the quantities $\partial \varGamma /\partial s$ and $\partial U/\partial s$ become infinite simultaneously at this clean point and resolve back to finite values for $t > t_*$ and the formerly clean point is now contaminated with surfactant. This interesting singularity is designated weak because, while certain derivative quantities exhibit instantaneous blow-up at $t_*$, the flow itself remains finite and continues to exist beyond $t_*$. Bickel & Detcheverry (2022) and Temprano-Coleto & Stone (2024) have recently used the complex Burgers equation formulation of Crowdy (2021b,c) to study such singularity formation in more detail by studying other solution types such as similarity solutions. Since the real Burgers equation is the paradigmatic nonlinear equation exhibiting shock formation in the absence of any (viscous) regularization, and since it is also known that there are circumstances in which ‘surfactant shocks’ can occur in Marangoni flows (Jensen & Grotberg 1992), it is natural to ask if any phenomena akin to shock formation are observable within the viscous Marangoni regime shown here to be describable by a complex-valued Burgers-type partial differential equation. Crowdy (2021b) briefly discussed this issue from the perspective of the more general question of well-posedness of solutions of the complex Burgers equation and suggested, based on empirical observations, that the physical requirement that $\varGamma \ge 0$ on the interface, which is specific to the Marangoni flow application, may preclude the formation of any finite-time singularities such as shocks. In very recent work, and by making associations with the more general literature on transport equations involving Hilbert transforms, Temprano-Coleto & Stone (2024) have offered evidence to support this suggestion. It should be noted that surfactant shock formation has been observed in quite different geometrical set-ups involving thin fluid layers (Jensen & Grotberg 1992) which is not a characteristic of the radial bubble geometry of the present paper, or in the previous work of Crowdy (2021b,c) where a mathematical description in terms of a complex Burgers equation was shown to be relevant to infinitely deep viscous fluid layers.

The availability of analytical solutions is valuable when adding in other effects perturbatively by assuming they are small. A few obvious extensions to the work here are to include the effect of weak inertia (small but non-zero Reynolds number), weak deformability of the bubble and weak solubility of the surfactant to the bulk.

Finally, since the connection of Marangoni dynamics to the complex Burgers equation was unveiled in the half-plane fluid geometry by Crowdy (2021b,c), several further theoretical advances have been made in the semi-infinite geometry (Bickel & Detcheverry 2022; Crowdy et al. 2023; Temprano-Coleto & Stone 2024). The present paper extends these new theoretical developments in a different direction, namely to the radial bubble geometry. It is likely that this new formulation will similarly pave the way for other advances in understanding Marangoni flows involving bubbles and droplets. Among additional physical effects that are amenable to a similar formulation are thermocapillarity (Young et al. 1959), reaction effects (Crowdy 2021b) and solubility of the surfactant (Crowdy et al. 2023) and progress in these directions will be reported elsewhere.