Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T04:00:24.680Z Has data issue: false hasContentIssue false
  • English
  • Français

Viscous drop in compressional Stokes flow

Published online by Cambridge University Press:  27 February 2013

Michael Zabarankin ,
Irina Smagin ,
Olga M. Lavrenteva  and
Avinoam Nir
Michael Zabarankin*
Affiliation:
Department of Mathematical Sciences, Stevens Institute of Technology, Castle Point on Hudson, Hoboken, NJ 07030, USA
Irina Smagin
Affiliation:
The Wolfson Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel
Olga M. Lavrenteva
Affiliation:
The Wolfson Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel
Avinoam Nir
Affiliation:
The Wolfson Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

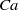The dynamics of the deformation of a drop in axisymmetric compressional viscous flow is addressed through analytical and numerical analyses for a variety of capillary numbers, $\mathit{Ca}$, and viscosity ratios, 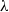$\lambda $. For low 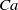$Ca$, the drop is approximated by an oblate spheroid, and an analytical solution is obtained in terms of spheroidal harmonics; whereas, for the case of equal viscosities (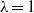$\lambda = 1$), the velocity field within and outside a drop of a given shape admits an integral representation, and steady shapes are found in the form of Chebyshev series. For arbitrary 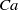$Ca$ and 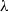$\lambda $, exact steady shapes are evaluated numerically via an integral equation. The critical 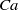$\mathit{Ca}$, below which a steady drop shape exists, is established for various 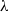$\lambda $. Remarkably, in contrast to the extensional flow case, critical steady shapes, being flat discs with rounded rims, have similar degrees of deformation (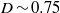$D\sim 0. 75$) for all 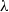$\lambda $ studied. It is also shown that for almost the entire range of 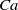$\mathit{Ca}$ and 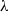$\lambda $, the steady shapes have accurate two-parameter approximations. The validity and implications of spheroidal and two-parameter shape approximations are examined in comparison to the exact steady shapes.

JFM classification

Mathematical Foundations: Computational methods Drops and Bubbles: Drops Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 720 , 10 April 2013 , pp. 169 - 191
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. & Lo, T. S. 1978 Deformation and breakup of a single slender drop in an extensional flow. J. Fluid. Mech. 86, 641–672.Google Scholar
Aris, R. 1962 Vectors, Tensors and Basic Equations of Fluid Mechanics. Prentice-Hall.Google Scholar
Barthès-Biesel, D. & Acrivos, A. 1973 Deformation and burst of a liquid droplet freely suspended in a linear shear field. J. Fluid Mech. 61, 1–21.CrossRefGoogle Scholar
Bazhlekov, I. B., Chesters, A. K. & van de Vosse, F. N. 2000 The effect of the dispersed to continuous-phase viscosity ratio on film drainage between interacting drops. Intl J. Multiphase Flow 26, 445–466.Google Scholar
Cox, R. G. 1969 Deformation of a drop in a general time-dependent fluid flow. J. Fluid Mech. 37, 601–623.Google Scholar
Davis, R. H. 1999 Buoyancy-driven viscous interaction of a rising drop with a smaller trailing drop. Phys. Fluids 11, 1016–1028.CrossRefGoogle Scholar
Eggleton, C. D. & Stebe, K. J. 1998 An adsorption–desorption-controlled surfactant on a deforming droplet. J. Colloid Interface Sci. 208, 68–80.Google Scholar
Frankel, A. N. & Acrivos, A. 1970 Constitutive equation for a dilute emulsion. J. Fluid Mech. 4, 65–78.Google Scholar
Happel, J. & Brenner, H. 1965 Low Reynolds Number Hydrodynamics. Nordhoff.Google Scholar
Hobson, E. W. 1955 The Theory of Spherical and Ellipsoidal Harmonics. Chelsea.Google Scholar
Hooper, R., Toose, M., Macosko, C. W. & Derby, J. J. 2001 A comparison of boundary element and finite element methods for modeling axisymmetric polymeric drop deformation. Intl J. Numer. Meth. Fluids 37, 837–864.Google Scholar
Kang, I. S. & Leal, L. G. 1989 Numerical solution of axisymmetric, unsteady free-boundary problems at finite Reynolds number. II. Deformation of a bubble in a biaxial straining flow. Phys. Fluids A 1, 644–660.Google Scholar
Lac, E. & Homsy, G. M. 2007 Axisymmetric deformation and stability of a viscous drop in a steady electric field. J. Fluid Mech. 590, 239–264.Google Scholar
Ladyzhenskaya, O. A. 1969 The Mathematical Theory of Viscous Incompressible Flow. Gordon and Breach.Google Scholar
Lavrenteva, O. M., Berezhnov, V. & Nir, A. 2002 Axisymmetric motion of a pair of deformable heavy drops in an upward temperature gradient. Phys. Fluids 14, 1326–1339.Google Scholar
Leal, L. G. 1992 Laminar Flow and Convective Transport Processes. Butterworth-Heinemann.Google Scholar
Levich, V. G. 1962 Physicochemical Hydrodynamics. Prentice-Hall.Google Scholar
Navot, Y. 1999 Critical behavior of drop breakup in axisymmetric viscous flow. Phys. Fluids 11, 990–996.CrossRefGoogle Scholar
Payne, L. E. & Pell, W. H. 1960 The Stokes flow problem for a class of axially symmetric bodies. J. Fluid Mech. 7, 529–549.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Rallison, J. M. & Acrivos, A. 1978 A numerical study of the deformation and burst of a viscous drop in an extensional flow. J. Fluid Mech. 89, 191–200.Google Scholar
Smagin, I., Pathak, M., Lavrenteva, O. M. & Nir, A. 2011 Motion and shape of an axisymmetric viscoplastic drop slowly falling through a viscous fluid. Rheol. Acta 50, 361–374.Google Scholar
Stone, H. A. 1994 Dynamics of drop deformation and breakup in viscous flow. Annu. Rev. Fluid Mech. 26, 65–102.CrossRefGoogle Scholar
Stone, H. A. & Leal, L. G. 1989 A note concerning drop deformation and breakup in biaxial extensional flows at low Reynolds numbers. J. Colloid Interface Sci. 133, 340–347.Google Scholar
Taylor, G. I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. A 146, 501–523.Google Scholar
Toose, E. M., Van den Ende, D., Geurts, B. J., Kuerten, J. G. M. & Zandbergen, P. J. 1996 Axisymmetric non-Newtonian drops treated with a boundary integral method. J. Engng Maths 30, 131–150.Google Scholar
Vlahovska, P. M., Loewenberg, M. & Blawzdziewicz, J. 2005 Deformation of a surfactant-covered drop in a linear flow. Phys. Fluids 17, 103103.CrossRefGoogle Scholar
Zabarankin, M. 2008 The framework of $k$ -harmonically analytic functions for three-dimensional Stokes flow problems, Part I. SIAM J. Appl. Maths 69, 845–880.Google Scholar
Zabarankin, M. & Molyboha, A. 2011 3D shape optimization in viscous incompressible fluid under Oseen approximation. SIAM J. Control Optim. 49, 1358–1382.CrossRefGoogle Scholar
Zabarankin, M. & Nir, A. 2011 Generalized analytic functions in an extensional Stokes flow with a deformable drop. SIAM J. Appl. Maths 71, 925–951.Google Scholar