Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T03:56:39.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Viscous boundary layer properties in turbulent thermal convection in a cylindrical cell: the effect of cell tilting

Published online by Cambridge University Press:  27 February 2013

Ping Wei  and
Ke-Qing Xia
Ping Wei
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Ke-Qing Xia*
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report an experimental study of the properties of the velocity boundary layer in turbulent Rayleigh–Bénard convection in a cylindrical cell. The measurements were made at Rayleigh numbers 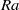$\mathit{Ra}$ in the range 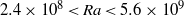$2. 4\times 1{0}^{8} \lt \mathit{Ra}\lt 5. 6\times 1{0}^{9} $ and were conducted with the convection cell tilted with an angle 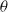$\theta $ relative to gravity, at 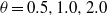$\theta = 0. 5, 1. 0, 2. 0$ and 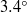$3. {4}^{\circ } $, respectively. The fluid was water with Prandtl number 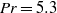$\mathit{Pr}= 5. 3$. It is found that at small tilt angles (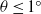$\theta \leq {1}^{\circ } $), the measured viscous boundary layer thickness 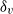${\delta }_{v} $ scales with the Reynolds number 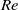$\mathit{Re}$ with an exponent close to that for a Prandtl–Blasius (PB) laminar boundary layer, i.e. 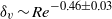${\delta }_{v} \sim {\mathit{Re}}^{- 0. 46\pm 0. 03} $. For larger tilt angles, the scaling exponent of 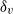${\delta }_{v} $ with 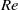$\mathit{Re}$ decreases with 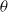$\theta $. The normalized mean horizontal velocity profiles measured at the same tilt angle but with different 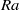$\mathit{Ra}$ are found to have an invariant shape. However, for different tilt angles, the shape of the normalized profiles is different. It is also found that the Reynolds number 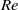$\mathit{Re}$ based on the maximum mean horizontal velocity scales with 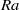$\mathit{Ra}$ as 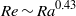$\mathit{Re}\sim {\mathit{Ra}}^{0. 43} $ and the Reynolds number 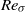${\mathit{Re}}_{\sigma } $ based on the maximum root mean square velocity scales with 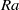$\mathit{Ra}$ as 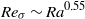${\mathit{Re}}_{\sigma } \sim {\mathit{Ra}}^{0. 55} $. Within the measurement resolution neither exponent depends on the tilt angle 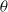$\theta $. Several wall quantities are also measured directly and their dependencies on 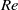$\mathit{Re}$ are found to agree well with those predicted for a classical laminar boundary layer. These are the wall shear stress $\tau $ (${\sim }{\mathit{Re}}^{1. 46} $), the viscous sublayer 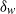${\delta }_{w} $ (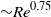${\sim }{\mathit{Re}}^{0. 75} $), the friction velocity 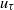${u}_{\tau } $ (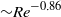${\sim }{\mathit{Re}}^{- 0. 86} $) and the skin friction coefficient 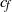${c}_{f} $ (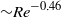${\sim }{\mathit{Re}}^{- 0. 46} $). Again, all of these near-wall quantities do not exhibit a dependence on the tilt angle within the measurement resolution. We also examined the dynamical scaling method proposed by Zhou and Xia (Phys. Rev. Lett., vol. 104, 2010, p. 104301) and found that in both the laboratory and the dynamical frames the mean velocity profiles show deviations from the theoretical PB profile, with the deviations increasing with 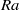$\mathit{Ra}$. However, profiles obtained from dynamical scaling in general have better agreement with the theoretical profile. It is also found that the effectiveness of this method appears to be independent of 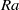$\mathit{Ra}$.

JFM classification

Convection: Buoyant boundary layers Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 720 , 10 April 2013 , pp. 140 - 168
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Brown, E. & Nikolaenko, A. 2006 The search for slow transients, and the effect of imperfect vertical alignment, in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 557, 347–367.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Ashkenazi, S. & Steinberg, V. 1999 High Rayleigh number turbulent convection in a gas near the gas–liquid critical point. Phys. Rev. Lett. 83, 3641–3644.CrossRefGoogle Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1993 Boundary layer length scales in thermal turbulence. Phys. Rev. Lett. 70, 4067–4070.CrossRefGoogle ScholarPubMed
Belmonte, A., Tilgner, A. & Libchaber, A. 1994 Temperature and velocity boundary layers in turbulent convection. Phys. Rev. E 50, 269–279.CrossRefGoogle ScholarPubMed
Brown, E., Funfschilling, D. & Ahlers, G. 2007 Anomalous Reynolds-number scaling in turbulent Rayleigh–Bénard convection. J. Stat. Mech. Theory E. 2007 (10), P10005.CrossRefGoogle Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.CrossRefGoogle ScholarPubMed
Chavanne, X., Chillà, F., Chabaud, B., Castaing, B. & Hébral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13 (5), 1300–1320.CrossRefGoogle Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 1–25.CrossRefGoogle ScholarPubMed
Dubrulle, B. 2001 Momentum transport and torque scaling in Taylor–Couette flow from an analogy with turbulent convection. Eur. Phys. J. B 21, 295.Google Scholar
Dubrulle, B. 2002 Scaling in large Prandtl number turbulent thermal convection. Eur. Phys. J. B 28, 361–367.CrossRefGoogle Scholar
du Puits, R., Resagk, C. & Thess, A. 2007a Mean velocity profile in confined turbulent convection. Phys. Rev. Lett. 99, 234504.CrossRefGoogle ScholarPubMed
du Puits, R., Resagk, C., Tilgner, A., Busse, F. H. & Thess, A. 2007b Structure of thermal boundary layers in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 572, 231–254.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.CrossRefGoogle Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34–39.CrossRefGoogle Scholar
Lam, S., Shang, X.-D., Zhou, S.-Q. & Xia, K.-Q. 2002 Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh–Bénard convection. Phys. Rev. E 65, 066306.CrossRefGoogle ScholarPubMed
Li, L., Shi, N., du Puits, R., Resagk, C., Schumacher, J. & Thess, A. 2012 Bounday layer analysis in turbulent Rayleigh–Bénard convection in air: experiment versus simulation. Phys. Rev. E 86, 026315.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Lui, S. L. & Xia, K.-Q. 1998 Spatial structure of the thermal boundary layer in turbulent convection. Phys. Rev. E 57, 5494–5503.CrossRefGoogle Scholar
Naert, A., Segawa, T. & Sano, M. 1997 High-Reynolds-number thermal turbulence in mercury. Phys. Rev. E 56, 1302–1305.CrossRefGoogle Scholar
Ni, R., Huang, S.-D. & Xia, K.-Q. 2011a Local energy dissipation rate balances local heat flux in the centre of turbulent thermal convection. Phys. Rev. Lett. 107, 174503.CrossRefGoogle ScholarPubMed
Ni, R., Huang, S.-D. & Xia, K.-Q. 2012 Lagrangian acceleration measurements in convective thermal turbulence. J. Fluid Mech. 692, 395–419.CrossRefGoogle Scholar
Ni, R., Zhou, S.-Q. & Xia, K.-Q. 2011b An experimental investigation of turbulent thermal convection in water-based alumina nanofluid. Phys. Fluids 23, 022005.CrossRefGoogle Scholar
Qiu, X.-L. & Xia, K.-Q. 1998a Spatial structure of the viscous boundary layer in turbulent convection. Phys. Rev. E 58, 5816.CrossRefGoogle Scholar
Qiu, X.-L. & Xia, K.-Q. 1998b Viscous boundary layers at the sidewall of a convection cell. Phys. Rev. E 58, 486.CrossRefGoogle Scholar
Scheel, J. D., Kim, E. & White, K. R. 2012 Thermal and viscous boundary layers in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 711, 281–305.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2000 Boundary Layer Theory. Springer.CrossRefGoogle Scholar
Shi, N., Emran, M. S. & Schumacher, J. 2012 Boundary layer structure in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 706, 5–33.CrossRefGoogle Scholar
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh number convection. Phys. Rev. A 42, 3650–3653.CrossRefGoogle ScholarPubMed
Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.CrossRefGoogle Scholar
Stevens, R. J. A. M., Zhou, Q., Grossmann, S., Verzicco, R., Xia, K.-Q. & Lohse, D. 2012 Thermal boundary layer profiles in turbulent Rayleigh–Bénard convection in a cylindrical sample. Phys. Rev. E 85, 027301.CrossRefGoogle Scholar
Sun, C., Cheung, Y.-H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.CrossRefGoogle Scholar
Sun, C., Xi, H.-D. & Xia, K.-Q. 2005a Azimuthal symmetry, flow dynamics, and heat flux in turbulent thermal convection in a cylinder with aspect ratio one-half. Phys. Rev. Lett. 95, 074502.CrossRefGoogle Scholar
Sun, C. & Xia, K.-Q. 2005 Scaling of the Reynolds number in turbulent thermal convection. Phys. Rev. E 72, 067302.CrossRefGoogle ScholarPubMed
Sun, C., Xia, K.-Q. & Tong, P. 2005b Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72, 026302.CrossRefGoogle Scholar
Sun, C., Zhou, Q. & Xia, K.-Q. 2006 Cascades of velocity and temperature fluctuations in buoyancy-driven turbulence. Phys. Rev. Lett. 97, 144504.CrossRefGoogle ScholarPubMed
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulence convection in water. Phys. Rev. E 47, 2253–2256.CrossRefGoogle ScholarPubMed
Verzicco, R. & Camussi, R. 1999 Prandtl number effects in convective turbulence. J. Fluid Mech. 383, 55–73.CrossRefGoogle Scholar
Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 447, 19–49.Google Scholar
Wang, J. & Xia, K.-Q. 2003 Spatial variations of the mean and statistical quantities in the thermal boundary layers of turbulent convection. Eur. Phys. J. B 32, 127–136.CrossRefGoogle Scholar
Wu, X.-Z. & Libcharber, A. 1991 Non-Boussinesq effects in free thermal convection. Phys. Rev. A 43, 2833–2839.CrossRefGoogle ScholarPubMed
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73, 056312.CrossRefGoogle ScholarPubMed
Xia, K.-Q., Sun, C. & Zhou, S.-Q. 2003 Particle image velocimetry measurement of the velocity field in turbulent thermal convection. Phys. Rev. E 68, 066303.CrossRefGoogle ScholarPubMed
Xia, K.-Q., Xin, Y.-B. & Tong, P. 1995 Dual-beam incoherent cross-correlation spectroscopy. J. Opt. Soc. Am. A 12, 1571.CrossRefGoogle Scholar
Xie, Y.-C., Wei, P. & Xia, K.-Q. 2013 Dynamics of the large-scale circulation in high Prandtl number turbulent thermal convection. J. Fluid Mech. 717, 322–346.CrossRefGoogle Scholar
Xin, Y.-B. & Xia, K.-Q. 1997 Boundary layer length scales in convective turbulence. Phys. Rev. E 56, 3010.CrossRefGoogle Scholar
Xin, Y.-B., Xia, K.-Q. & Tong, P. 1996 Boundary layers in turbulent convection. Phys. Rev. Lett. 77, 1266.CrossRefGoogle ScholarPubMed
Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
Zhou, Q., Sugiyama, K., Stevens, R. J. A. M., Grossmann, S., Lohse, D. & Xia, K.-Q. 2011 Horizontal structures of velocity and temperature boundary layers in two-dimensional numerical turbulent Rayleigh–Bénard convection. Phys. Fluids 23, 125104.CrossRefGoogle Scholar
Zhou, Q., Sun, C. & Xia, K.-Q. 2008 Experimental investigation of homogeneity, isotropy, and circulation of the velocity field in buoyancy-driven turbulence. J. Fluid. Mech. 598, 361–372.CrossRefGoogle Scholar
Zhou, S.-Q. & Xia, K.-Q. 2002 Plume statistics in thermal turbulence: mixing of an active scalar. Phys. Rev. Lett. 89, 184502.CrossRefGoogle ScholarPubMed
Zhou, Q. & Xia, K.-Q. 2010 Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 104301.CrossRefGoogle ScholarPubMed