Article contents
Viscoelastic liquid curtains: experimental results on the flow of a falling sheet of polymer solution
Published online by Cambridge University Press: 24 June 2019
Abstract
We experimentally investigate the extensional flow of a sheet – or curtain – of viscoelastic liquid falling freely from a slot at constant flow rate under gravity. Extruded liquids are aqueous solutions of flexible polyethylene oxide (PEO) and of semi-rigid partially hydrolysed polyacrylamide (HPAM) with low shear viscosities. Velocimetry measurements reveal that the mean velocity field 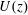 $U(z)$ (where
$U(z)$ (where  $z$ is the distance from the slot exit) does not reduce to a free fall. More precisely, we show that the liquid falls initially with sub-gravitational accelerations up to a distance from the slot which scales as
$z$ is the distance from the slot exit) does not reduce to a free fall. More precisely, we show that the liquid falls initially with sub-gravitational accelerations up to a distance from the slot which scales as 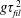 $g\unicode[STIX]{x1D70F}_{fil}^{2}$ (where
$g\unicode[STIX]{x1D70F}_{fil}^{2}$ (where 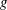 $g$ is gravity and
$g$ is gravity and 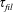 $\unicode[STIX]{x1D70F}_{fil}$ is the extensional relaxation time of the liquid) due to the stretching of polymer molecules. Beyond this elastic length, inertia dominates and the local acceleration reaches the asymptotic free-fall value
$\unicode[STIX]{x1D70F}_{fil}$ is the extensional relaxation time of the liquid) due to the stretching of polymer molecules. Beyond this elastic length, inertia dominates and the local acceleration reaches the asymptotic free-fall value 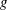 $g$. The length of the sub-gravitational part of the curtain is shown to be much larger than the equivalent viscous length
$g$. The length of the sub-gravitational part of the curtain is shown to be much larger than the equivalent viscous length 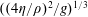 $((4\unicode[STIX]{x1D702}/\unicode[STIX]{x1D70C})^{2}/g)^{1/3}$ for Newtonian liquids of density
$((4\unicode[STIX]{x1D702}/\unicode[STIX]{x1D70C})^{2}/g)^{1/3}$ for Newtonian liquids of density 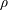 $\unicode[STIX]{x1D70C}$ and dynamic viscosity
$\unicode[STIX]{x1D70C}$ and dynamic viscosity 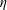 $\unicode[STIX]{x1D702}$ which is usually small compared to the curtain length. By analogy with Newtonian curtains, we show that the velocity field
$\unicode[STIX]{x1D702}$ which is usually small compared to the curtain length. By analogy with Newtonian curtains, we show that the velocity field 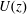 $U(z)$ rescales on a master curve. Besides, the flow is shown to be only weakly affected by the history of polymer deformations in the die upstream of the curtain. Furthermore, investigations on the curtain stability reveal that polymer addition reduces the minimum flow rate required to maintain a continuous sheet of liquid.
$U(z)$ rescales on a master curve. Besides, the flow is shown to be only weakly affected by the history of polymer deformations in the die upstream of the curtain. Furthermore, investigations on the curtain stability reveal that polymer addition reduces the minimum flow rate required to maintain a continuous sheet of liquid.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 11
- Cited by



