Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-15T18:59:44.546Z Has data issue: false hasContentIssue false
  • English
  • Français

Viscoelastic effects on the deformation and breakup of a droplet on a solid wall in Couette flow

Published online by Cambridge University Press:  16 May 2023

Ningning Wang ,
Sheng Li ,
Liang Shi ,
Xuefeng Yuan  and
Haihu Liu Open the ORCID record for Haihu Liu [Opens in a new window]
Ningning Wang
Affiliation:
School of Energy and Power Engineering, Xi'an Jiaotong University, 28 West Xianning Road, Xi'an 710049, PR China
Sheng Li
Affiliation:
School of Energy and Power Engineering, Xi'an Jiaotong University, 28 West Xianning Road, Xi'an 710049, PR China
Liang Shi
Affiliation:
Heilongjiang Provincial Key Laboratory of Reservoir Physics and Fluid Mechanics in Porous Medium, Daqing 163712, PR China
Xuefeng Yuan
Affiliation:
Institute for Systems Rheology, Guangzhou University, 230 West Outer Ring Road, Guangzhou 510006, PR China
Haihu Liu*
Affiliation:
School of Energy and Power Engineering, Xi'an Jiaotong University, 28 West Xianning Road, Xi'an 710049, PR China Heilongjiang Provincial Key Laboratory of Reservoir Physics and Fluid Mechanics in Porous Medium, Daqing 163712, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

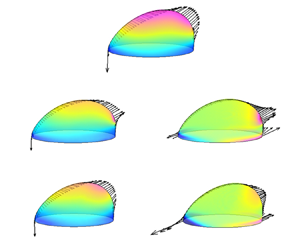
The deformation, movement and breakup of a wall-attached droplet subject to Couette flow are systematically investigated using an enhanced lattice Boltzmann colour-gradient model, which accounts for not only the viscoelasticity (described by the Oldroyd-B constitutive equation) of either droplet (V/N) or matrix fluid (N/V) but also the surface wettability. We first focus on the steady-state deformation of a sliding droplet for varying values of capillary number ($Ca$), Weissenberg number ($Wi$) and solvent viscosity ratio ($\beta$). Results show that the relative wetting area $A_r$ in the N/V system is increased by either increasing $Ca$, or by increasing $Wi$ or decreasing $\beta$, where the former is attributed to the increased viscous force and the latter to the enhanced elastic effects. In the V/N system, however, $A_r$ is restrained by the droplet elasticity, especially at higher $Wi$ or lower $\beta$, and the inhibiting effect strengthens with an increase of $Ca$. Decreasing $\beta$ always reduces droplet deformation when either fluid is viscoelastic. The steady-state droplet motion is quantified by the contact-line capillary number $Ca_{cl}$, and a force balance is established to successfully predict the variations of $Ca_{cl}/Ca$ with $\beta$ for each two-phase viscosity ratio in both N/V and V/N systems. The droplet breakup is then studied for varying $Wi$. The critical capillary number of droplet breakup monotonically increases with $Wi$ in the N/V system, while it first increases, then decreases and finally reaches a plateau in the V/N system.

JFM classification

Non-Newtonian Flows: Viscoelasticity Multiphase and Particle-laden Flows: Multiphase flow Interfacial Flows (free surface): Contact lines
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 963 , 25 May 2023 , A18
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Afkhami, S., Yue, P. & Renardy, Y. 2009 A comparison of viscoelastic stress wakes for two-dimensional and three-dimensional Newtonian drop deformations in a viscoelastic matrix under shear. Phys.Fluids 21 (7), 072106.CrossRefGoogle Scholar
Aggarwal, N. & Sarkar, K. 2007 Deformation and breakup of a viscoelastic drop in a Newtonian matrix under steady shear. J.Fluid Mech. 584, 1–21.CrossRefGoogle Scholar
Aggarwal, N. & Sarkar, K. 2008 Effects of matrix viscoelasticity on viscous and viscoelastic drop deformation in a shear flow. J.Fluid Mech. 601, 63–84.CrossRefGoogle Scholar
Alves, M.A., Oliveira, P.J. & Pinho, F.T. 2020 Numerical methods for viscoelastic fluid flows. Annu. Rev. Fluid Mech. 53 (1), 1–33.Google Scholar
Boyko, E. & Stone, H.A. 2022 Pressure-driven flow of the viscoelastic Oldroyd-B fluid in narrow non-uniform geometries: analytical results and comparison with simulations. J.Fluid Mech. 936, A23.CrossRefGoogle Scholar
Brackbill, J.U., Kothe, D.B. & Zemach, C. 1992 A continuum method for modeling surface tension. J.Comput. Phys. 100 (2), 335–354.CrossRefGoogle Scholar
Chen, Z., Shu, C., Liu, Y. & Zhang, L. 2021 Ternary phase-field simplified multiphase Lattice Boltzmann method and its application to compound droplet dynamics on solid surface in shear flow. Phys.Rev. Fluids 6 (9), 094304.CrossRefGoogle Scholar
Dimitrakopoulos, P. & Higdon, J.J.L. 1997 Displacement of fluid droplets from solid surfaces in low-Reynolds-number shear flows. J.Fluid Mech. 336, 351–378.CrossRefGoogle Scholar
Ding, H., Gilani, M.N.H. & Spelt, P.D.M. 2010 Sliding, pinch-off and detachment of a droplet on a wall in shear flow. J.Fluid Mech. 644, 217–244.CrossRefGoogle Scholar
Ding, H. & Spelt, P.D.M. 2007 Wetting condition in diffuse interface simulations of contact line motion. Phys.Rev. E 75 (4), 046708.CrossRefGoogle ScholarPubMed
Ding, H. & Spelt, P.D.M. 2008 Onset of motion of a three-dimensional droplet on a wall in shear flow at moderate Reynolds numbers. J.Fluid Mech. 599, 341–362.CrossRefGoogle Scholar
Dussan, E.B. 1979 On the spreading of liquids on solid surfaces: static and dynamic contact lines. Annu. Rev. Fluid Mech. 11 (1), 371–400.CrossRefGoogle Scholar
Elmendorp, J.J. 1986 A study on polymer blending microrheology. Polym. Engng Sci. 26 (6), 418–426.CrossRefGoogle Scholar
Flumerfelt, R.W. 1972 Drop breakup in simple shear fields of viscoleastic fluids. Ind. Engng Chem. Fundam. 11 (3), 312–318.CrossRefGoogle Scholar
de Gennes, P.G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863.CrossRefGoogle Scholar
Guido, S., Simeone, M. & Greco, F. 2003 Deformation of a Newtonian drop in a viscoelastic matrix under steady shear flow: experimental validation of slow flow theory. J.Non-Newtonian Fluid Mech. 114 (1), 65–82.CrossRefGoogle Scholar
Gunstensen, A., Rothman, D., Zaleski, S. & Zanetti, G. 1991 Lattice Boltzmann model of immiscible fluids. Phys.Rev. A 43, 4320–4327.CrossRefGoogle ScholarPubMed
Gupta, A. & Sbragaglia, M. 2014 Deformation and breakup of viscoelastic droplets in confined shear flow. Phys.Rev. E 90 (2), 023305.CrossRefGoogle ScholarPubMed
Gupta, A. & Sbragaglia, M. 2015 Deformation and break-up of viscoelastic droplets using Lattice Boltzmann models. Proc. IUTAM 15, 215–227.CrossRefGoogle Scholar
Halliday, I., Hollis, A.P. & Care, C.M. 2007 Lattice Boltzmann algorithm for continuum multicomponent flow. Phys.Rev. E 76 (2), 026708.CrossRefGoogle ScholarPubMed
Halliday, I., Law, R., Care, C.M. & Hollis, A. 2006 Improved simulation of drop dynamics in a shear flow at low Reynolds and Capillary number. Phys.Rev. E 73 (5), 056708.CrossRefGoogle Scholar
Han, J. & Kim, C. 2014 Theoretical and experimental studies on the contact line motion of second-order fluid. Rheol. Acta 53 (1), 55–66.CrossRefGoogle Scholar
Han, Y., Han, L., He, L., Wang, S. & Luo, X. 2021 Universal criterion for critical motion of droplets adhered on surfaces with different wettability in laminar flow. Ind. Engng Chem. Res. 60 (8), 3397–3410.CrossRefGoogle Scholar
Hu, T., Fu, Q., Xing, Y., Yang, L. & Xie, L. 2021 Stability of a thin viscoelastic film falling down an inclined plane. Phys.Rev. Fluids 6 (8), 083902.CrossRefGoogle Scholar
Huang, J., Huang, H. & Wang, X. 2014 Numerical study of drop motion on a surface with stepwise wettability gradient and contact angle hysteresis. Phys.Fluids 26 (6), 062101.CrossRefGoogle Scholar
Jacqmin, D. 2000 Contact-line dynamics of a diffuse fluid interface. J.Fluid Mech. 402, 57–88.CrossRefGoogle Scholar
Ladd, A.J.C. 1994 Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J.Fluid Mech. 271, 285–309.CrossRefGoogle Scholar
Liu, H., Zhang, J., Ba, Y., Wang, N. & Wu, L. 2020 Modelling a surfactant-covered droplet on a solid surface in three-dimensional shear flow. J.Fluid Mech. 897, A33.CrossRefGoogle Scholar
Liu, H.-R., Gao, P. & Ding, H. 2017 Fluid–structure interaction involving dynamic wetting: 2d modeling and simulations. J.Comput. Phys. 348, 45–65.CrossRefGoogle Scholar
Liu, Y., Fan, J., Liu, L. & Yang, S. 2018 Numerical simulation of residual oil flooded by polymer solution in microchannels. Geofluids 2018, 8947839.CrossRefGoogle Scholar
Lu, X., Cao, B., Xie, K., Cao, W., Liu, Y., Zhang, Y., Wang, X. & Zhang, J. 2021 Enhanced oil recovery mechanisms of polymer flooding in a heterogeneous oil reservoir. Petrol. Explor. Dev. 48 (1), 169–178.CrossRefGoogle Scholar
Ma, J., Wang, Z., Young, J., Lai, J.C.S., Sui, Y. & Tian, F. 2020 An immersed boundary-Lattice Boltzmann method for fluid-structure interaction problems involving viscoelastic fluids and complex geometries. J.Comput. Phys. 415, 109487.CrossRefGoogle Scholar
Maffettone, P.L. & Greco, F. 2003 Ellipsoidal drop model for single drop dynamics with non-Newtonian fluids. J.Rheol. 48 (1), 83–100.CrossRefGoogle Scholar
Malaspinas, O., Fiétier, N. & Deville, M. 2010 Lattice Boltzmann method for the simulation of viscoelastic fluid flows. J.Non-Newtonian Fluid Mech. 165 (23), 1637–1653.CrossRefGoogle Scholar
Mighri, F., Carreau, P.J. & Ajji, A. 1998 Influence of elastic properties on drop deformation and breakup in shear flow. J.Rheol. 42 (6), 1477–1490.CrossRefGoogle Scholar
Min, Q., Duan, Y., Wang, X., Liang, Z., Lee, D. & Su, A. 2010 Spreading of completely wetting, non-Newtonian fluids with non-power-law rheology. J.Colloid. Interface Sci. 348 (1), 250–254.CrossRefGoogle ScholarPubMed
Minetti, C., Audemar, V., Podgorski, T. & Coupier, G. 2019 Dynamics of a large population of red blood cells under shear flow. J.Fluid Mech. 864, 408–448.CrossRefGoogle Scholar
Mukherjee, S. & Sarkar, K. 2009 Effects of viscosity ratio on deformation of a viscoelastic drop in a Newtonian matrix under steady shear. J.Non-Newtonian Fluid Mech. 160 (2), 104–112.CrossRefGoogle Scholar
Oldroyd, J.G. 1950 On the formulation of rheological equations of state. Proc. R. Soc. Lond. A 200 (1063), 523–541.Google Scholar
Poole, R. 2012 The Deborah and Weissenberg numbers. Brit. Soc. Rheol. 53, 32–39.Google Scholar
Ramaswamy, S. & Leal, L.G. 1999 The deformation of a viscoelastic drop subjected to steady uniaxial extensional flow of a Newtonian fluid. J.Non-Newtonian Fluid Mech. 85 (2), 127–163.CrossRefGoogle Scholar
Rock, A., Hincapie, R.E., Tahir, M., Langanke, N. & Ganzer, L. 2020 On the role of polymer viscoelasticity in enhanced oil recovery: extensive laboratory data and review. Polymers 12 (10), 2276.CrossRefGoogle ScholarPubMed
Shikhmurzaev, Y.D. 1993 The moving contact line on a smooth solid surface. Intl J. Multiphase Flow 19 (4), 589–610.CrossRefGoogle Scholar
Souas, F., Safri, A. & Benmounah, A. 2021 A review on the rheology of heavy crude oil for pipeline transportation. Petrol. Res. 6 (2), 116–136.CrossRefGoogle Scholar
Spelt, P.D.M. 2006 Shear flow past two-dimensional droplets pinned or moving on an adhering channel wall at moderate Reynolds numbers: a numerical study. J.Fluid Mech. 561, 439–463.CrossRefGoogle Scholar
Su, J, Ouyang, J, Wang, X., Yang, B. & Zhou, W. 2013 Lattice Boltzmann method for the simulation of viscoelastic fluid flows over a large range of Weissenberg numbers. J.Non-Newtonian Fluid Mech. 194, 42–59.CrossRefGoogle Scholar
Subhedar, A., Reiter, A., Selzer, M., Varnik, F. & Nestler, B. 2020 Interface tracking characteristics of color-gradient Lattice Boltzmann model for immiscible fluids. Phys.Rev. E 101, 013313.CrossRefGoogle ScholarPubMed
Sui, Y., Ding, H. & Spelt, P.D.M. 2014 Numerical simulations of flows with moving contact lines. Annu. Rev. Fluid Mech. 46 (1), 97–119.CrossRefGoogle Scholar
Varagnolo, S., Filippi, D., Mistura, G., Pierno, M. & Sbragaglia, M. 2017 Stretching of viscoelastic drops in steady sliding. Soft Matt. 13 (17), 3116–3124.CrossRefGoogle ScholarPubMed
Varanasi, P.P., Ryan, M.E. & Stroeve, P. 1994 Experimental study on the breakup of model viscoelastic drops in uniform shear flow. Ind. Engng Chem. Res. 33 (7), 1858–1866.CrossRefGoogle Scholar
Varchanis, S., Tsamopoulos, J., Shen, A.Q. & Haward, S.J. 2022 Reduced and increased flow resistance in shear-dominated flows of Oldroyd-B fluids. J.Non-Newtonian Fluid Mech. 300, 104698.CrossRefGoogle Scholar
Venkatesan, J. & Ganesan, S. 2019 Computational modeling of impinging viscoelastic droplets. J.Non-Newtonian Fluid Mech. 263, 42–60.CrossRefGoogle Scholar
Verhulst, K., Cardinaels, R., Moldenaers, P., Renardy, Y. & Afkhami, S. 2009 Influence of viscoelasticity on drop deformation and orientation in shear flow. Part 1. Stationary states. J.Non-Newtonian Fluid Mech. 156 (1), 29–43.CrossRefGoogle Scholar
Verhulst, K., Moldenaers, P. & Minale, M. 2007 Drop shape dynamics of a Newtonian drop in a non-Newtonian matrix during transient and steady shear flow. J.Rheol. 51 (2), 261–273.CrossRefGoogle Scholar
Wang, D., Tan, D.S., Khoo, B.C., Ouyang, Z. & Phan-Thien, N. 2020 a A Lattice Boltzmann modeling of viscoelastic drops’ deformation and breakup in simple shear flows. Phys.Fluids 32 (12), 123101.CrossRefGoogle Scholar
Wang, D., Wang, N. & Liu, H. 2022 Droplet deformation and breakup in shear-thinning viscoelastic fluid under simple shear flow. J.Rheol. 66 (3), 585–603.CrossRefGoogle Scholar
Wang, L., Huang, H. & Lu, X. 2013 Scheme for contact angle and its hysteresis in a multiphase Lattice Boltzmann method. Phys.Rev. E 87 (1), 013301.CrossRefGoogle Scholar
Wang, N., Semprebon, C., Liu, H., Zhang, C. & Kusumaatmaja, H. 2020 b Modelling double emulsion formation in planar flow-focusing microchannels. J.Fluid Mech. 895, A22.CrossRefGoogle Scholar
Wang, Y., Do-Quang, M. & Amberg, G. 2015 Dynamic wetting of viscoelastic droplets. Phys.Rev. E 92 (4), 043002.CrossRefGoogle ScholarPubMed
Wang, Y., Do-Quang, M. & Amberg, G. 2017 Impact of viscoelastic droplets. J.Non-Newtonian Fluid Mech. 243, 38–46.CrossRefGoogle Scholar
Xie, C., Qi, P., Xu, K., Xu, J. & Balhoff, M.T. 2022 Oscillative trapping of a droplet in a converging channel induced by elastic instability. Phys.Rev. Lett. 128 (5), 054502.CrossRefGoogle Scholar
Ye, H., Shen, Z. & Li, Y. 2018 Cell stiffness governs its adhesion dynamics on substrate under shear flow. IEEE Trans. Nanotechnol. 17 (3), 407–411.CrossRefGoogle Scholar
Yeganehdoust, F., Amer, A., Sharifi, N., Karimfazli, I. & Dolatabadi, A. 2021 Droplet mobility on slippery lubricant impregnated and superhydrophobic surfaces under the effect of air shear flow. Langmuir 37 (20), 6278–6291.CrossRefGoogle ScholarPubMed
Yue, P., Feng, J.J., Liu, C. & Shen, J. 2005 Viscoelastic effects on drop deformation in steady shear. J.Fluid Mech. 540, 427–437.CrossRefGoogle Scholar
Zou, S., Yuan, X., Yang, X., Yi, W. & Xu, X. 2014 An integrated Lattice Boltzmann and finite volume method for the simulation of viscoelastic fluid flows. J.Non-Newtonian Fluid Mech. 211, 99–113.CrossRefGoogle Scholar