Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wu Yu
Yi Shi-He
He Lin
Quan Peng-Cheng
and
Zhu Yang-Zhu
2015.
Quantitative analysis of flow structures in compression ramp based on flow visualization.
Acta Physica Sinica,
Vol. 64,
Issue. 1,
p.
014703.
Yang, Shao-Qiong
Li, Shan
Tian, Hai-Ping
Wang, Qing-Yi
and
Jiang, Nan
2016.
Tomographic PIV investigation on coherent vortex structures over shark-skin-inspired drag-reducing riblets.
Acta Mechanica Sinica,
Vol. 32,
Issue. 2,
p.
284.
Farano, Mirko
Cherubini, Stefania
Robinet, Jean-Christophe
and
De Palma, Pietro
2017.
Optimal bursts in turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 817,
Issue. ,
p.
35.
Hara, Shumpei
Ii, Ryusuke
Tsukahara, Takahiro
and
Kawaguchi, Yasuo
2017.
Analysis of an organized turbulent structure using a pattern recognition technique in a drag-reducing surfactant solution flow.
International Journal of Heat and Fluid Flow,
Vol. 63,
Issue. ,
p.
56.
Wang, Qian-cheng
Wang, Zhen-guo
and
Zhao, Yu-xin
2017.
The impact of streamwise convex curvature on the supersonic turbulent boundary layer.
Physics of Fluids,
Vol. 29,
Issue. 11,
Deng, Sichao
Pan, Chong
Wang, Jinjun
and
He, Guosheng
2018.
On the spatial organization of hairpin packets in a turbulent boundary layer at low-to-moderate Reynolds number.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
635.
Iacobello, G.
Scarsoglio, S.
Kuerten, J. G. M.
and
Ridolfi, L.
2018.
Spatial characterization of turbulent channel flow via complex networks.
Physical Review E,
Vol. 98,
Issue. 1,
Farano, M.
Cherubini, S.
De Palma, P.
and
Robinet, J.-C.
2018.
Nonlinear optimal large-scale structures in turbulent channel flow.
European Journal of Mechanics - B/Fluids,
Vol. 72,
Issue. ,
p.
74.
Li, Weipeng
and
Wang, Lipo
2018.
Geometrical structure analysis of a zero-pressure-gradient turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 846,
Issue. ,
p.
318.
Wang, Wenkang
Pan, Chong
and
Wang, Jinjun
2018.
Wall-Normal Variation of Spanwise Streak Spacing in Turbulent Boundary Layer With Low-to-Moderate Reynolds Number.
Entropy,
Vol. 21,
Issue. 1,
p.
24.
Wang, Wenkang
Pan, Chong
and
Wang, Jinjun
2018.
Quasi-bivariate variational mode decomposition as a tool of scale analysis in wall-bounded turbulence.
Experiments in Fluids,
Vol. 59,
Issue. 1,
Yao, Jie
and
Hussain, Fazle
2019.
Supersonic turbulent boundary layer drag control using spanwise wall oscillation.
Journal of Fluid Mechanics,
Vol. 880,
Issue. ,
p.
388.
Bai, Xiao-dong
Zhang, Wei
Fang, Qing-he
Wang, Yong
Zheng, Jin-hai
and
Guo, An-xin
2019.
The visualization of turbulent coherent structure in open channel flow.
Journal of Hydrodynamics,
Vol. 31,
Issue. 2,
p.
266.
Li, Weipeng
and
Liu, Hong
2019.
Two-point statistics of coherent structures in turbulent flow over riblet-mounted surfaces.
Acta Mechanica Sinica,
Vol. 35,
Issue. 3,
p.
457.
Li, Shan
Jiang, Nan
and
Yang, Shao-Qiong
2019.
Influence of sinusoidal riblets on the coherent structures in turbulent boundary layer studied by time-resolved particle image velocimetry.
Acta Physica Sinica,
Vol. 68,
Issue. 7,
p.
074702.
Li, Xin
Tong, Fu-Lin
Yu, Chang-Ping
and
Li, Xin-Liang
2020.
Correlation between density and temperature fluctuations of hypersonic turbulent boundary layers at Ma∞ = 8.
AIP Advances,
Vol. 10,
Issue. 7,
Li, Weipeng
2020.
Turbulence statistics of flow over a drag-reducing and a drag-increasing riblet-mounted surface.
Aerospace Science and Technology,
Vol. 104,
Issue. ,
p.
106003.
Li, Zexiang
Dang, Xiangxin
Lv, Pengyu
and
Duan, Huiling
2021.
Blowing-only opposition control: Characteristics of turbulent drag reduction and implementation by deep learning.
AIP Advances,
Vol. 11,
Issue. 3,
2023.
Multi-layered turbulence structure of flow under free surface of open channel flow using velocity–vorticity correlation structure method.
Physics of Fluids,
Vol. 35,
Issue. 5,
Liu, Chunye
Wang, Wene
Hu, Xiaotao
Fang, Juan
and
Liu, Fulai
2023.
The Roles of Riblet and Superhydrophobic Surfaces in Energy Saving Using a Spatial Correlation Analysis.
Nanomaterials,
Vol. 13,
Issue. 5,
p.
875.
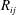 $R_{ij}$ of velocity and vorticity components,
$R_{ij}$ of velocity and vorticity components, 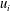 $u_i$ and
$u_i$ and  $\omega _j~ (i, j = 1, 2, 3)$, is proposed as a useful descriptor of CS. For turbulent channel flow with the wall-normal direction
$\omega _j~ (i, j = 1, 2, 3)$, is proposed as a useful descriptor of CS. For turbulent channel flow with the wall-normal direction 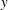 $y$, a VVCS study consists of using
$y$, a VVCS study consists of using 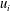 $u_i$ at a fixed reference location
$u_i$ at a fixed reference location 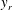 $y_r$, and using
$y_r$, and using 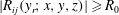 $|R_{ij} (y_r; x, y, z)|\geqslant R_0$ to define a topologically invariant high-correlation region, called
$|R_{ij} (y_r; x, y, z)|\geqslant R_0$ to define a topologically invariant high-correlation region, called 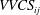 $\mathit{VVCS}_{ij}$. The method is applied to direct numerical simulation (DNS) data, and it is shown that the
$\mathit{VVCS}_{ij}$. The method is applied to direct numerical simulation (DNS) data, and it is shown that the 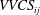 $\mathit{VVCS}_{ij}$ qualitatively and quantitatively captures all known geometrical features of near-wall CS, including spanwise spacing, streamwise length and inclination angle of the quasi-streamwise vortices and streaks. A distinct feature of the VVCS is that its geometry continuously varies with
$\mathit{VVCS}_{ij}$ qualitatively and quantitatively captures all known geometrical features of near-wall CS, including spanwise spacing, streamwise length and inclination angle of the quasi-streamwise vortices and streaks. A distinct feature of the VVCS is that its geometry continuously varies with 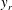 $y_r$. A topological change of
$y_r$. A topological change of 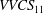 $\mathit{VVCS}_{11}$ from quadrupole (for smaller
$\mathit{VVCS}_{11}$ from quadrupole (for smaller 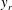 $y_r$) to dipole (for larger
$y_r$) to dipole (for larger 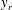 $y_r$) occurs at
$y_r$) occurs at 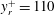 $y^{+}_r=110$, giving a geometrical interpretation of the multilayer nature of wall-bounded turbulent shear flows. In conclusion, the VVCS provides a new robust method to quantify CS in wall-bounded flows, and is particularly suitable for extracting statistical geometrical measures using two-point simultaneous data from hotwire, particle image velocimetry/laser Doppler anemometry measurements or DNS/large eddy simulation data.
$y^{+}_r=110$, giving a geometrical interpretation of the multilayer nature of wall-bounded turbulent shear flows. In conclusion, the VVCS provides a new robust method to quantify CS in wall-bounded flows, and is particularly suitable for extracting statistical geometrical measures using two-point simultaneous data from hotwire, particle image velocimetry/laser Doppler anemometry measurements or DNS/large eddy simulation data.