Hostname: page-component-5cf477f64f-2wr7h Total loading time: 0 Render date: 2025-04-07T06:18:19.953Z Has data issue: false hasContentIssue false
  • English
  • Français

Variable-density mixing in turbulent jets with coflow

Published online by Cambridge University Press:  24 July 2017

John J. Charonko  and
Katherine Prestridge Open the ORCID record for Katherine Prestridge [Opens in a new window]
John J. Charonko*
Affiliation:
Physics Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
Katherine Prestridge
Affiliation:
Physics Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

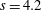Two sets of experiments are performed to study variable-density effects in turbulent round jets with coflow at density ratios, $s=4.2$ and 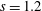$s=1.2$. Ten thousand instantaneous realisations of simultaneous two-dimensional particle image velocimetry and planar laser-induced fluorescence at three axial locations in the momentum-dominated region of the jet allow us to calculate the full turbulent kinetic energy (t.k.e.) budgets, providing insights into the mechanisms of density fluctuation correlations both axially and radially in a non-Boussinesq flow. The strongest variable-density effects are observed within the velocity half-width of the jet, 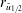$r_{\tilde{u} _{1/2}}$. Variable-density effects decrease the Reynolds stresses via increased turbulent mass flux in the heavy jet, as shown by previous jet centreline measurements. Radial profiles of turbulent flux show that in the lighter jet t.k.e. is moving away from the centreline, while in the heavy jet it is being transported both inwards towards the centreline and radially outwards. Negative t.k.e. production is observed in the heavy jet, and we demonstrate that this is caused by both reduced gradient stretching in the axial direction and increased turbulent mass fluxes. Large differences in advection are also observed between the two jets. The air jet has higher total advection caused by strong axial components, while density fluctuations in the heavy jet reduce the axial advection significantly. The budget mechanisms in the non-Boussinesq regime are best understood using effective density and velocity half-width, 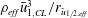$\unicode[STIX]{x1D70C}_{eff}\bar{u}_{1,CL}^{3}/r_{\tilde{u} _{1/2,eff}}$, a modification of previous scaling.

JFM classification

Convection: Buoyancy-driven instability Wakes/Jets: Jets Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 825 , 25 August 2017 , pp. 887 - 921
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amendt, P., Landen, O. L., Robey, H. F., Li, C. K. & Petrasso, R. D. 2010 Plasma barodiffusion in inertial-confinement-fusion implosions: application to observed yield anomalies in thermonuclear fuel mixtures. Phys. Rev. Lett. 105 (11), 115005.CrossRefGoogle ScholarPubMed
Amielh, M., Djeridane, T., Anselmet, F. & Fulachier, L. 1996 Velocity near-field of variable density turbulent jets. Intl J. Heat Mass Transfer 39 (10), 2149–2164.CrossRefGoogle Scholar
Balakumar, B. J., Orlicz, G. C., Ristorcelli, J. R., Balasubramanian, S., Prestridge, K. P. & Tomkins, C. D. 2012 Turbulent mixing in a Richtmyer–Meshkov fluid layer after reshock: velocity and density statistics. J. Fluid Mech. 696, 67–93.CrossRefGoogle Scholar
Besnard, D., Harlow, F. H., Rauenzahn, R. M. & Zemach, C.1992 Turbulence transport equations for variable-density turbulence and their relationship to two-field models. Tech. Rep. LA-12303-MS. Los Alamos National Laboratory, New Mexico (United States).CrossRefGoogle Scholar
Boersma, B. J., Brethouwer, G. & Nieuwstadt, F. T. M. 1998 A numerical investigation on the effect of the inflow conditions on the self-similar region of a round jet. Phys. Fluids 10, 899–909.CrossRefGoogle Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structures in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.CrossRefGoogle Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2006 The route to self-similarity in turbulent jets and plumes. J. Fluid Mech. 547, 137–148.CrossRefGoogle Scholar
Cebeci, T. & Smith, A. M. O. 1974 Analysis of Turbulent Boundary Layers. (Applied Mathematics and Mechanics) , vol. 15. Academic.Google Scholar
Charonko, J. J. & Vlachos, P. P. 2013 Estimation of uncertainty bounds for individual particle image velocimetry measurements from cross-correlation peak ratio. Meas. Sci. Technol. 24 (6), 065301.CrossRefGoogle Scholar
Chassaing, P., Antonia, R. A., Anselmet, F., Joly, L. & Sarkar, S. 2002 Variable Density Fluid Turbulence, Fluid Mechanics and Its Applications, vol. 69. Springer.CrossRefGoogle Scholar
Chassaing, P., Harran, G. & Joly, L. 1994 Density fluctuation correlations in free turbulent binary mixing. J. Fluid Mech. 279, 239–278.CrossRefGoogle Scholar
Chen, C. J. & Rodi, W. 1980 Vertical Turbulent Buoyant Jets: A Review of Experimental Data. HMT - Science and Applications of Heat and Mass Transfer, vol. 4. Pergamon.Google Scholar
Coleman, H. W. & Steele, W. G. 2009 Experimentation, Validation, and Uncertainty Analysis for Engineers, 3rd edn. Wiley.CrossRefGoogle Scholar
Darisse, A., Lemay, J. & Benaïssa, A. 2015 Budgets of turbulent kinetic energy, Reynolds stresses, variance of temperature fluctuations and turbulent heat fluxes in a round jet. J. Fluid Mech. 774, 95–142.CrossRefGoogle Scholar
Dimotakis, P. E. 1986 Two-dimensional shear-layer entrainment. AIAA J. 24 (11), 1791–1796.CrossRefGoogle Scholar
Djeridane, T., Amielh, M., Anselmet, F. & Fulachier, L. 1996 Velocity turbulence properties in the near-field region of axisymmetric variable density jets. Phys. Fluids 8 (6), 1614–1630.CrossRefGoogle Scholar
Eckstein, A. & Vlachos, P. P. 2009a Assessment of advanced windowing techniques for digital particle image velocimetry (DPIV). Meas. Sci. Technol. 20 (7), 075402.Google Scholar
Eckstein, A. & Vlachos, P. P. 2009b Digital particle image velocimetry (DPIV) robust phase correlation. Meas. Sci. Technol. 20 (5), 055401.Google Scholar
Fischer, H. B. 1979 Mixing in Inland and Coastal Waters. Academic.Google Scholar
George, W. K., Arndt, R. E. & Corrsin, S. 1988 Advances in Turbulence, pp. 39–73. CRC Press.Google Scholar
Gerashchenko, S. & Prestridge, K. 2015 Density and velocity statistics in variable density turbulent mixing. J. Turbul. 16 (11), 1011–1035.CrossRefGoogle Scholar
Harran, G., Chassaing, P., Joly, L. & Chibat, M. 1996 Etude numérique des effets de densité dans un jet de mélange turbulent en microgravité. Rev. Gén. Therm. 35 (411), 151–176.CrossRefGoogle Scholar
Herant, M., Benz, W., Hix, W. R., Fryer, C. L. & Colgate, S. A. 1994 Inside the supernova: a powerful convective engine. Astrophys. J. 435, 339–361.CrossRefGoogle Scholar
Hussein, H. J., Capp, S. P. & George, W. K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.CrossRefGoogle Scholar
International Organization for Standardization 1995 Guide to the Expression of Uncertainty in Measurement, 2nd edn. International Organization for Standardization.Google Scholar
Kähler, C. J., Sammler, B. & Kompenhans, J. 2004 Generation and control of tracer particles for optical flow investigations in air. In Particle Image Velocimetry: Recent Improvements (ed. Stanislas, M., Westerweel, J. & Kompenhans, J.), pp. 417–426. Springer.CrossRefGoogle Scholar
Laufer, J. 1952 The structure of turbulence in fully developed pipe flow. Natl Bur. Stand. 1174, 1–18.Google Scholar
Lee, J. H.-W. & Chu, V. H. 2003 Turbulent Jets and Plumes: A Lagrangian Approach. Kluwer.CrossRefGoogle Scholar
Lindl, J. D., McCrory, R. L. & Campbell, E. M. 1992 Progress toward ignition and burn propagation in inertial confinement fusion. Phys. Today 45 (9), 32–40.CrossRefGoogle Scholar
Livescu, D. & Ristorcelli, J. R. 2007 Buoyancy-driven variable-density turbulence. J. Fluid Mech. 591, 43–71.CrossRefGoogle Scholar
Livescu, D. & Ristorcelli, J. R. 2008 Variable-density mixing in buoyancy-driven turbulence. J. Fluid Mech. 605, 145–180.CrossRefGoogle Scholar
Lumley, J. L. 1979 Computational modeling of turbulent flows. Adv. Appl. Mech. 18, 123–176.CrossRefGoogle Scholar
O’Hern, T. J., Weckman, E. J., Gerhart, A. L., Tieszen, S. R. & Schefer, R. W. 2005 Experimental study of a turbulent buoyant helium plume. J. Fluid Mech. 544, 143–171.CrossRefGoogle Scholar
Panchapakesan, N. R. & Lumley, J. L. 1993a Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 197–223.CrossRefGoogle Scholar
Panchapakesan, N. R. & Lumley, J. L. 1993b Turbulence measurements in axisymmetric jets of air and helium. Part 2. Helium jet. J. Fluid Mech. 246, 225–247.CrossRefGoogle Scholar
Pitts, W. M.1986 Effects of global density and Reynolds number variations on mixing in turbulent, axisymmetric jets. National Bureau of Standards report NBSIR 86–3340. National Bureau of Standards, US Department of Commerce, Gaithersburg, MD.CrossRefGoogle Scholar
Pitts, W. M. 1991a Effects of global density ratio on the centerline mixing behavior of axisymmetric turbulent jets. Exp. Fluids 11 (2–3), 125–134.CrossRefGoogle Scholar
Pitts, W. M. 1991b Reynolds number effects on the mixing behavior of axisymmetric turbulent jets. Exp. Fluids 11 (2–3), 135–141.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows, 1st edn. Cambridge University Press.CrossRefGoogle Scholar
Richards, C. D. & Pitts, W. M. 1993 Global density effects on the self-preservation behaviour of turbulent free jets. J. Fluid Mech. 254, 417–435.CrossRefGoogle Scholar
Sarathi, P., Gurka, R., Kopp, G. A. & Sullivan, P. J. 2011 A calibration scheme for quantitative concentration measurements using simultaneous PIV and PLIF. Exp. Fluids 52 (1), 247–259.CrossRefGoogle Scholar
Sautet, J. C. & Stepowski, D. 1995 Dynamic behavior of variable-density, turbulent jets in their near development fields. Phys. Fluids 7 (11), 2796–2806.CrossRefGoogle Scholar
Schwarzkopf, J. D., Livescu, D., Gore, R. A., Rauenzahn, R. M. & Ristorcelli, J. R. 2011 Application of a second-moment closure model to mixing processes involving multicomponent miscible fluids. J. Turbul. 12, N49.CrossRefGoogle Scholar
Schwarzkopf, J. D., Livescu, D., Baltzer, J. R., Gore, R. A. & Ristorcelli, J. R. 2016 A two-length scale turbulence model for single-phase multi-fluid mixing. Flow Turbul. Combust. 96, 1–43.CrossRefGoogle Scholar
Sciacchitano, A. & Wieneke, B. 2016 PIV uncertainty propagation. Meas. Sci. Technol. 27 (8), 084006.CrossRefGoogle Scholar
Soteriou, M. C. & Ghoniem, A. F. 1995 Effects of the free-stream density ratio on free and forced spatially developing shear layers. Phys. Fluids 7 (8), 2036–2051.CrossRefGoogle Scholar
Talbot, B., Mazellier, N., Renou, B., Danaila, L. & Boukhalfa, M. A. 2009 Time-resolved velocity and concentration measurements in variable-viscosity turbulent jet flow. Exp. Fluids 47 (4–5), 769–787.CrossRefGoogle Scholar
Thring, M. W. & Newby, M. P. 1953 Combustion length of enclosed turbulent jet flames. In Symposium (International) on Combustion, vol. 4, pp. 789–796. Elsevier.Google Scholar
Thurber, M. C.1999 Acetone laser-induced fluorescence for temperature and multiparameter imaging in gaseous flows. Topical Rep. TSD-120. U.S. Air Force Office of Scientific Research, Stanford University.Google Scholar
Uddin, M. & Pollard, A. 2007 Self-similarity of coflowing jets: the virtual origin. Phys. Fluids 19, 068103.CrossRefGoogle Scholar
Van Cruyningen, I., Lozano, A. & Hanson, R. K. 1990 Quantitative imaging of concentration by planar laser-induced fluorescence. Exp. Fluids 10 (1), 41–49.CrossRefGoogle Scholar
Wang, H. & Law, A.W.-K. 2002 Second-order integral model for a round turbulent buoyant jet. J. Fluid Mech. 459, 397–428.CrossRefGoogle Scholar
Webster, D. R., Roberts, P. J. W. & Ra’ad, L. 2001 Simultaneous DPTV/PLIF measurements of a turbulent jet. Exp. Fluids 30 (1), 65–72.CrossRefGoogle Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39 (6), 1096–1100.CrossRefGoogle Scholar
Wilson, B. M. & Smith, B. L. 2013 Uncertainty on PIV mean and fluctuating velocity due to bias and random errors. Meas. Sci. Technol. 24 (3), 035302.CrossRefGoogle Scholar
Wu, X. & Moin, P. 2008 A direct numerical simulation study on the mean velocity characteristics of turbulent pipe flow. J. Fluid Mech. 608, 81–112.CrossRefGoogle Scholar
Wygnanski, I. & Fiedler, H. 1969 Some measurements in the self-preserving jet. J. Fluid Mech. 38 (03), 577–612.CrossRefGoogle Scholar
Zingale, M., Almgren, A. S., Bell, J. B., Nonaka, A. & Woosley, S. E. 2009 Low Mach number modeling of type IA supernovae. IV. White dwarf convection. Astrophys. J. 704, 196–210.CrossRefGoogle Scholar