No CrossRef data available.
Article contents
Vapour explosion under hot water depressurization
Published online by Cambridge University Press: 22 December 2016
Abstract
This paper continues a series of works developing a model for a high-speed boiling flow capable of describing different fluxes with no change in the model coefficients. Refining the interfacial area transport equation in partial derivatives, we test the ability of the model to describe phenomena that cannot be simulated by models that average the interfacial interaction. In the previous version, the possibility for bubble fragmentation was considered, which permitted us to reproduce an explosive boiling in rarefaction shocks moving at a speed of 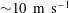 ${\sim}10~\text{m}~\text{s}^{-1}$ fixed in experiments on hot water decompression. The shocks were shown to be caused by a chain bubble fragmentation leading to a sharp increase in the interphase area (Ivashnyov et al., J. Fluid Mech., vol. 413, 2000, pp. 149–180). With no change in the free parameters (the initial number of boiling centres in the flow bulk and the critical Weber number) chosen for a tube decompression, the model gave close predictions for critical flows in long nozzles,
${\sim}10~\text{m}~\text{s}^{-1}$ fixed in experiments on hot water decompression. The shocks were shown to be caused by a chain bubble fragmentation leading to a sharp increase in the interphase area (Ivashnyov et al., J. Fluid Mech., vol. 413, 2000, pp. 149–180). With no change in the free parameters (the initial number of boiling centres in the flow bulk and the critical Weber number) chosen for a tube decompression, the model gave close predictions for critical flows in long nozzles, 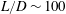 $L/D\sim 100$. The formation of a boiling shock in the nozzle was shown to be the reason for the onset of autovibrated regimes (Ivashnyov & Ivashneva, J. Fluid Mech., vol. 710, 2012, pp. 72–101). However, the previous model does not simulate the phenomenon of a vapour explosion at a primary stage of a hot water decompression, when the first rarefaction wave is followed by an extended, 1 m width, several MPa amplitude compression wave in which the pressure reaches a plateau below a saturation value. The model proposed assumes initial boiling centre origination at the channel walls. Due to overflowing, the wall bubbles break up, with their fragments passing into the flow. On growing up, the flow bubbles can break up in their turn. It is shown that an extended compression wave is caused by the fragmentation of wall bubbles, which leads to the increase in the interphase area, boiling intensification and the pressure rise. The pressure reaches a plateau before a saturation state is reached due to flow momentum loss accelerating the fragments of wall bubbles. The phenomenon of pressure ‘oscillation’ fixed in some experimental oscillograms when the pressure in the compression wave increases up to a saturation pressure and then drops to the plateau value has been explained as well. The ‘illposedness’ defect of the generally accepted model for two-phase two-velocity flow with a compressible carrying phase, which lies in its complex characteristics, has been rectified. The calculations of a stationary countercurrent liquid-particle flow in a diffuser with the improved hyperbolic model predicts a critical regime with a maximal liquid mass flux, while the old non-hyperbolic model simulates the supercritical regimes with ‘numerical instabilities’. Calculations of a transient upward flow of particles have shown the formation of a superslow ‘creeping’ shock wave of particles compacting.
$L/D\sim 100$. The formation of a boiling shock in the nozzle was shown to be the reason for the onset of autovibrated regimes (Ivashnyov & Ivashneva, J. Fluid Mech., vol. 710, 2012, pp. 72–101). However, the previous model does not simulate the phenomenon of a vapour explosion at a primary stage of a hot water decompression, when the first rarefaction wave is followed by an extended, 1 m width, several MPa amplitude compression wave in which the pressure reaches a plateau below a saturation value. The model proposed assumes initial boiling centre origination at the channel walls. Due to overflowing, the wall bubbles break up, with their fragments passing into the flow. On growing up, the flow bubbles can break up in their turn. It is shown that an extended compression wave is caused by the fragmentation of wall bubbles, which leads to the increase in the interphase area, boiling intensification and the pressure rise. The pressure reaches a plateau before a saturation state is reached due to flow momentum loss accelerating the fragments of wall bubbles. The phenomenon of pressure ‘oscillation’ fixed in some experimental oscillograms when the pressure in the compression wave increases up to a saturation pressure and then drops to the plateau value has been explained as well. The ‘illposedness’ defect of the generally accepted model for two-phase two-velocity flow with a compressible carrying phase, which lies in its complex characteristics, has been rectified. The calculations of a stationary countercurrent liquid-particle flow in a diffuser with the improved hyperbolic model predicts a critical regime with a maximal liquid mass flux, while the old non-hyperbolic model simulates the supercritical regimes with ‘numerical instabilities’. Calculations of a transient upward flow of particles have shown the formation of a superslow ‘creeping’ shock wave of particles compacting.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press



