Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-19T07:52:46.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Valley ventilation by cross winds

Published online by Cambridge University Press:  19 April 2006

Robert C. Bell  and
Rory O. R. Y. Thompson
Robert C. Bell
Affiliation:
C.S.I.R.O. Division of Atmospheric Physics, P.O. Box 77, Mordialloc, Victoria, Australia 3195
Rory O. R. Y. Thompson
Affiliation:
C.S.I.R.O. Division of Atmospheric Physics, P.O. Box 77, Mordialloc, Victoria, Australia 3195
Get access Rights & Permissions [Opens in a new window]

Abstract

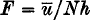An initial thermal stratification may be swept out of a valley if a cross-wind is strong enough: the valley is then said to be ventilated. Numerical and laboratory experiments indicate that the critical parameter is the Froude number, , where 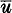is the mean horizontal velocity above the crest of the valley sides, N is the Brunt–Väisälä or bouyancy frequency of the thermal stratification in the valley air and h is the height of the valley walls. Ventilation occurs whenever the Froude number exceeds a value of 1·3.

Type
Research Article
Information
Journal of Fluid Mechanics , Volume 96 , Issue 4 , 27 February 1980 , pp. 757 - 767
Copyright
Copyright © 1980 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Present address: C.S.I.R.O. Division of Fisheries and Oceanography, P.O. Box 21, Cronulla, N.S.W., Australia, 2230.

References

Arakawa, A. 1966 Computational design for long-term numerical integration of the equations of fluid motion: two-dimensional incompressible flow. Part 1. J. Comput. Phys. 1, 119–143.10.1016/0021-9991(66)90015-5CrossRefGoogle Scholar
Ashe, W. F. 1952 Acute effects of air pollution in Donora, Pennsylvania. In Air Pollution (ed. McCabe, L. C.), pp. 455–462. McGraw-Hill.Google Scholar
Baines, P. G. 1977 Upstream influence and Long's model in stratified flows. J. Fluid Mech. 82, 147–160.10.1017/S0022112077000573CrossRefGoogle Scholar
Cox, R. A. 1977 Field studies of local weather and its effects on air pollution at a proposed industrial site. Weather 32, 42–56.CrossRefGoogle Scholar
Geiger, R. 1965 The Climate Near the Ground. Cambridge, Massachusetts: Harvard University Press.Google Scholar
Green, R. A. 1970 The weather and circulation of November, 1969. Monthly Weather Rev. 98, 170–174.10.1175/1520-0493(1970)098<0170:TWACON>2.3.CO;22.3.CO;2>CrossRefGoogle Scholar
Kaps, E. 1955 Zur Frage der Durchlüftung von Tälern im Mittelgebirge. Meteorol. Runds. 8, 61–65.Google Scholar
Kitabayashi, K. 1977 Wind tunnel and field studies of stagnant flow upstream of a ridge. J. Met. Soc. Japan 55, 193–204.10.2151/jmsj1965.55.2_193CrossRefGoogle Scholar
Mahrer, Y. & Pielke, R. A. 1978 A test of an upstream spline interpolation technique for the advective terms in a numerical mesoscale model. Monthly Weather Rev. 106, 818–830.10.1175/1520-0493(1978)106<0818:ATOAUS>2.0.CO;22.0.CO;2>CrossRefGoogle Scholar
Roache, P. J. 1972 Computational Fluid Dynamics. Albuquerque, New Mexico: Hermosa.Google Scholar
Tang, W. 1976 Theoretical study of cross-valley wind circulation. Arch. Met. Geophys. Bioklim. A 25, 1–18.10.1007/BF02245465CrossRefGoogle Scholar
Thompson, R. O. R. Y. 1979 A stable third-order time-integration method with minimal storage. Submitted to Monthly Weather Rev.Google Scholar
Thyer, N. H. 1966 A theoretical explanation of mountain and valley winds by a numerical model. Arch. Met. Geophys Bioklim. A 15, 318–348.10.1007/BF02247220CrossRefGoogle Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.CrossRefGoogle Scholar
Yoshino, M. 1957 The structure of surface winds crossing over a small valley. J. Met. Soc. Japan 35, 184–195.10.2151/jmsj1923.35.3_184CrossRefGoogle Scholar