Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T15:59:51.225Z Has data issue: false hasContentIssue false
  • English
  • Français

Validation and modification of asymptotic analysis of slow and rapid droplet spreading by numerical simulation

Published online by Cambridge University Press:  09 January 2013

Yi Sui  and
Peter D. M. Spelt
Yi Sui*
Affiliation:
Department of Chemical Engineering, Imperial College London, London SW7 2AZ, UK School of Engineering and Materials Science, Queen Mary University of London, London E1 4NS, UK
Peter D. M. Spelt
Affiliation:
Laboratoire de la Mécanique des Fluides et d’Acoustique, CNRS, Ecully, France Département Mécanique, Université Claude Bernard Lyon 1, Villeurbanne, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using a slip-length-based level-set approach with adaptive mesh refinement, we have simulated axisymmetric droplet spreading for a dimensionless slip length down to 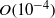$O(1{0}^{\ensuremath{-} 4} )$. The main purpose is to validate, and where necessary improve, the asymptotic analysis of Cox (J. Fluid Mech., vol. 357, 1998, pp. 249–278) for rapid droplet spreading/dewetting, in terms of the detailed interface shape in various regions close to the moving contact line and the relation between the apparent angle and the capillary number based on the instantaneous contact-line speed, 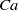$\mathit{Ca}$. Before presenting results for inertial spreading, simulation results are compared in detail with the theory of Hocking & Rivers (J. Fluid Mech., vol. 121, 1982, pp. 425–442) for slow spreading, showing that these agree very well (and in detail) for such small slip-length values, although limitations in the theoretically predicted interface shape are identified; a simple extension of the theory to viscous exterior fluids is also proposed and shown to yield similar excellent agreement. For rapid droplet spreading, it is found that, in principle, the theory of Cox can predict accurately the interface shapes in the intermediate viscous sublayer, although the inviscid sublayer can only be well presented when capillary-type waves are outside the contact-line region. However, 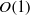$O(1)$ parameters taken to be unity by Cox must be specified and terms be corrected to 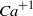${\mathit{Ca}}^{+ 1} $ in order to achieve good agreement between the theory and the simulation, both of which are undertaken here. We also find that the apparent angle from numerical simulation, obtained by extrapolating the interface shape from the macro region to the contact line, agrees reasonably well with the modified theory of Cox. A simplified version of the inertial theory is proposed in the limit of negligible viscosity of the external fluid. Building on these results, weinvestigate the flow structure near the contact line, the shear stress and pressure along the wall, and the use of the analysis for droplet impact and rapid dewetting. Finally, we compare the modified theory of Cox with a recent experiment for rapid droplet spreading, the results of which suggest a spreading-velocity-dependent dynamic contact angle in the experiments. The paper is closed with a discussion of the outlook regarding the potential of using the present results in large-scale simulations wherein the contact-line region is not resolved down to the slip length, especially for inertial spreading.

JFM classification

Interfacial Flows (free surface): Contact lines Drops and Bubbles: Drops and Bubbles Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 283 - 313
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afkhami, S., Zaleski, S. & Bussmann, M. 2009 A mesh-dependent model for applying dynamic contact angles to VOF simulations. J. Comput. Phys. 228, 5370–5389.Google Scholar
Bayer, I. S. & Megaridis, C. M. 2006 Contact angle dynamics in droplets impacting on flat surfaces with different wetting characteristics. J. Fluid Mech. 558, 415–449.Google Scholar
Bazhlekov, I. B. & Chesters, A. K. 1996 Numerical investigation of the dynamic influence of the contact line region on the macroscopic meniscus shape. J. Fluid Mech. 329, 137–146.Google Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81, 739–805.Google Scholar
Bussmann, M., Mostaghimi, J. & Chandra, S. 1999 On a three-dimensional volume tracking model of droplet impact. Phys. Fluids 11, 1406–1417.Google Scholar
Chen, Q., Ramé, E. & Garoff, S. 1997 The velocity field near moving contact lines. J. Fluid Mech. 337, 49–66.Google Scholar
Christodoulou, K. N. & Scriven, L. E. 1992 Discretization of free surface flows and other moving boundary problems. J. Comput. Phys. 99, 39–55.Google Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169.Google Scholar
Cox, R. G. 1998 Inertial and viscous effects on dynamic contact angles. J. Fluid Mech. 357, 249–278.Google Scholar
David, R. & Neumann, A. W. 2010 Computation of contact lines on randomly heterogeneous surfaces. Langmuir 26, 13256–13262.Google Scholar
De Gennes, P. G. 1986 Deposition of Langmuir–Blodgett layers. Colloid Polym. Sci. 264, 463–465.Google Scholar
Devauchelle, o., Josserand, C. & Zaleski, S. 2007 Forced dewetting on porous media. J. Fluid Mech. 574, 343–364.Google Scholar
Ding, H., Gilani, M. N. H. & Spelt, P. D. M. 2010 Sliding, pinchoff and detachment of a droplet on a wall in shear flow. J. Fluid Mech. 644, 217–244.Google Scholar
Ding, H., Li, E. Q., Zhang, F. H., Sui, Y., Spelt, P. D. M. & Thoroddsen, S. T. 2012 Ejection of small droplets in rapid drop spreading. J. Fluid Mech. 697, 92–114.Google Scholar
Ding, H. & Spelt, P. D. M. 2007 Inertial effects in droplet spreading: a comparison between diffuse interface and level-set simulations. J. Fluid Mech. 576, 287–296.CrossRefGoogle Scholar
Ding, H. & Spelt, P. D. M. 2008 Onset of motion of a 3D droplet on a wall in shear flow at moderate Reynolds numbers. J. Fluid Mech. 599, 341–362.Google Scholar
Ding, H., Spelt, P. D. M. & Shu, C. 2007 Diffuse interface model for incompressible two-phase flows with large density ratios. J. Comput. Phys. 226, 2078–2095.Google Scholar
Dussan V., E. B. & Davis, S. H. 1974 On the motion of a fluidfluid interface along a solid surface. J. Fluid Mech. 65, 71–95.Google Scholar
Eggers, J. 2004 Hydrodynamic theory of forced dewetting. Phys. Rev. Lett. 93, 094502.Google Scholar
Eggers, J. & Stone, H. A. 2004 Characteristic lengths at moving contact lines for a perfectly wetting fluid: the influence of speed on the dynamic contact angle. J. Fluid Mech. 505, 309–321.Google Scholar
Ertas, D. & Kardar, M. 1994 Critical dynamics of contact line depinning. Phys. Rev. E 49, R2532–R2535.Google Scholar
Fermigier, M. & Jenffer, P. 1990 An experimental investigation of the dynamic contact angle in liquid–liquid systems. J. Colloid Interface Sci. 146, 226–241.Google Scholar
Foister, R. T. 1990 The kinetics of displacement wetting in liquid/liquid/solid systems. J. Colloid Interface Sci. 136, 266–282.Google Scholar
Fuentes, J. & Cerro, R. L. 2005 Flow patterns and interfacial velocities near a moving contact line. Exp. Fluids 38, 505–510.Google Scholar
Fukai, J., Shilba, Y., Yamamoto, T., Miyatake, O., Poulikakos, D., Megaridis, C. M. & Zhao, Z. 1995 Wetting effects on the spreading of a liquid droplet colliding with a flat surface: experiment and modeling. Phys. Fluids 7, 236–247.Google Scholar
Greenspan, H. P. 1978 On the motion of a small viscous droplet that wets a surface. J. Fluid Mech. 84, 125–143.Google Scholar
Hocking, L. M. 1977 A moving fluid interface. Part 2. The removal of the force singularity by a slip flow. J. Fluid Mech. 79, 209–229.CrossRefGoogle Scholar
Hocking, L. M. 1983 The spreading of a thin drop by gravity and capillarity. Q. J. Mech. Appl. Maths 36, 55–69.Google Scholar
Hocking, L. M. & Rivers, A. D. 1982 The spreading of a drop by capillary action. J. Fluid Mech. 121, 425–442.Google Scholar
Huh, C. & Mason, S. G. 1977 The steady movement of a liquid meniscus in a capillary tube. J. Fluid Mech. 81, 401–419.Google Scholar
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35, 85–101.CrossRefGoogle Scholar
Jacqmin, D. 2000 Contact-line dynamics of a diffuse fluid interface. J. Fluid Mech. 402, 57–88.Google Scholar
Jiang, X. & James, A. J. 2007 Numerical simulation of the head-on collision of two equal-sized drops with van der Waals forces. J. Engng Maths 59, 99–121.Google Scholar
Kafka, F. Y. & Dussan V., E. B. 1979 On the interpretation of dynamic contact angles in capillaries. J. Fluid Mech. 95, 539–565.Google Scholar
Kolinski, J. M., Rubinstein, S. M., Mandre, S., Brenner, M. P., Weitz, D. A. & Mahadevan, L. 2012 Skating on a film of air: drops impacting on a surface. Phys. Rev. Lett. 108, 074503.Google Scholar
Landau, L. D. & Levich, B. V. 1942 Dragging of a liquid by a moving plate. Acta Physicochim. USSR 17, 42–54.Google Scholar
Le Grand, N., Daerr, A. & Limat, L. 2005 Shape and motion of drops sliding down an inclined plane. J. Fluid Mech. 541, 293–315.Google Scholar
Liu, X. D., Osher, S. & Chan, T. 1994 Weighted essentially non-oscillatory schemes. J. Comput. Phys. 115, 200–212.Google Scholar
Lowndes, J. 1980 The numerical simulation of the steady movement of a fluid meniscus in a capillary tube. J. Fluid Mech. 101, 631–646.CrossRefGoogle Scholar
MacNeice, P., Olson, K. M., Mobarry, C., deFainchtein, R. & Packer, C. 2000 PARAMESH: a parallel adaptive mesh refinement community toolkit. Comput. Phys. Commun. 126, 330–354.Google Scholar
Marsh, J. A., Garoff, S. & Dussan V., E. B. 1993 Dynamic contact angles and hydrodynamics near a moving contact line. Phys. Rev. Lett. 70, 2778–2781.Google Scholar
Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18, 1–18.Google Scholar
Pismen, L. M. & Pomeau, Y. 2000 Disjoining potential and spreading of thin liquid layers in the diffuse-interface model coupled to hydrodynamics. Phys. Rev. E 62, 2480–2492.Google Scholar
Qian, T., Wang, X.-P. & Sheng, P. 2003 Molecular scale contact line hydrodynamics of immiscible flows. Phys. Rev. E 564, 333–360.Google Scholar
Qian, T., Wang, X.-P. & Sheng, P. 2006 A variational approach to moving contact line hydrodynamics. J. Fluid Mech. 564, 333–360.Google Scholar
Ren, W. & E, W. 2007 Boundary conditions for the moving contact line problem. Phys. Fluids 68, 016306.Google Scholar
Renardy, Y., Popinet, S., Duchemin, L., Renardy, M., Zaleski, S., Josserand, C., Drumright-Clarke, M. A., Richard, D., Clanet, C. & Quéré, D. 2003 Pyramidal and toroidal water drops after impact on a solid surface. J. Fluid Mech. 484, 69–83.Google Scholar
Renardy, M., Renardy, Y. & Li, J. 2001 Numerical simulation of moving contact line problems using a volume-of-fluid method. J. Comput. Phys. 171, 243–263.Google Scholar
Savelski, M. J., Shetty, S. A., Kolb, W. B. & Cerro, R. L. 1995 Flow patterns associated with the steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 176, 117–127.Google Scholar
Savva, N. & Kalliadasis, S. 2011 Dynamics of moving contact lines: a comparison between slip and precursor film models. Eur. Phys. Lett. 94, 64004.Google Scholar
Sheng, P. & Zhou, M. 1992 Immiscible-fluid displacement: contact-line dynamics and the velocity-dependent capillary pressure. Phys. Rev. A 45, 5694–5708.Google Scholar
Shikhmurzaev, Y. D. 1993 The moving contact line on a smooth solid surface. Intl J. Multiphase Flow 19, 589–610.Google Scholar
Sibley, D. N., Savva, N. & Kalliadasis, S. 2012 Slip or no slip? A methodical examination of the interface formation model using two-dimensional droplet spreading on a horizontal planar substrate as a prototype system. Phys. Fluids 24, 082105.Google Scholar
Spelt, P. D. M. 2005 A level-set approach for simulations of flows with multiple moving contact lines with hysteresis. J. Comput. Phys. 207, 389–404.Google Scholar
Spelt, P. D. M. 2006 Shear flow past two-dimensional droplets pinned or moving on an adhering channel wall at moderate Reynolds numbers: a numerical study. J. Fluid Mech. 561, 439–463.Google Scholar
Stoev, K., Ramé, E. & Garoff, S. 1999 Effects of inertia on the hydrodynamics near moving contact lines. Phys. Fluids 11, 3209–3216.Google Scholar
Sussman, M., Almgren, A. S., Bell, J. B., Colella, P., Howell, L. H. & Welcome, M. L. 1999 An adaptive level set approach for incompressible two-phase flows. J. Comput. Phys. 148, 81–124.Google Scholar
Taylor, G. I. 1962 On scraping viscous fluid from a plane surface. In Miszellaneen der Angewandten Mechanik (Festschrift Walter Tollmien) (ed. Schäffer, M.), pp. 313–315. Akademie. See also The Scientific Papers of G. I. Taylor (ed. G. K. Batchelor), vol. IV, pp. 410–413.Google Scholar
Yarin, A. L. 2006 Drop impact dynamics: splashing, spreading, receding, bouncing …. Annu. Rev. Fluid Mech. 38, 159–192.Google Scholar
Yue, P., Zhou, C. & Feng, J. J. 2010 Sharp-interface limit of the CahnHilliard model for moving contact lines. J. Fluid Mech. 645, 279–294.Google Scholar