Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-19T12:13:57.150Z Has data issue: false hasContentIssue false
  • English
  • Français

Using functional gains for effective sensor location in flow control: a reduced-order modelling approach

Published online by Cambridge University Press:  28 September 2015

Imran Akhtar ,
Jeff Borggaard ,
John A. Burns ,
Haroon Imtiaz  and
Lizette Zietsman
Imran Akhtar*
Affiliation:
Department of Mechanical Engineering, NUST College of Electrical and Mechanical Engineering, National University of Sciences & Technology, Islamabad 44000, Pakistan
Jeff Borggaard
Affiliation:
Interdisciplinary Center for Applied Mathematics MC0531, Virginia Tech, Blacksburg, VA 24061, USA
John A. Burns
Affiliation:
Interdisciplinary Center for Applied Mathematics MC0531, Virginia Tech, Blacksburg, VA 24061, USA
Haroon Imtiaz
Affiliation:
Department of Mechanical Engineering, NUST College of Electrical and Mechanical Engineering, National University of Sciences & Technology, Islamabad 44000, Pakistan
Lizette Zietsman
Affiliation:
Interdisciplinary Center for Applied Mathematics MC0531, Virginia Tech, Blacksburg, VA 24061, USA
*
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The problem of active feedback control of fluid flows falls into a class of problems in the area of distributed parameter control. Distributed parameter systems are typically defined by partial differential equations that model the time and spatial evolution of the process. We consider the problem of locating sensors for effective feedback control of a fluid flow problem described by the Navier–Stokes equations. In this setting, the state of the system is the velocity field 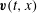$\boldsymbol{v}(t,x)$, and hence all feedback laws are a function of this velocity field or, in most practical settings, a function of sensor outputs. In many designs, the feedback control law can be represented as a linear function of the state defined by an integral operator with a kernel function called the functional gain. In this paper we show that these functional gains can be used to determine effective sensor placement in complex flow control applications. The approach is to choose measurements of the state that would provide good quadrature points for the integral operator. We provide a computational validation of this approach by controlling the vortex shedding in a two-dimensional cylinder flow using a pair of fluid actuators on the cylinder surface. This model is linearized about the mean flow and a feedback control is designed by pole placement. Distributed parameter control theory yields the existence and form of the functional gains which are used to locate sensors. In particular, we use the location of the supports of the functional gains to determine two sets of four sensor locations in the wake. One of these measurement sets coincides with large magnitudes of the gain and the other set coincides with small magnitudes. Numerical experiments with a reduced-order model confirm superior performance of the closed-loop (CL) system using the former sensor set. We also show that choosing sensor locations associated with small magnitudes of the functional gains actually destabilizes the CL system.

JFM classification

Flow Control: Flow Control Nonlinear Dynamical Systems: Low-dimensional models Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 781 , 25 October 2015 , pp. 622 - 656
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ackermann, J. E. 1977 On the synthesis of linear control systems with specified characteristics. Automatica 13 (1), 89–94.Google Scholar
Akhtar, I.2008 Parallel simulations, reduced-order modeling, and feedback control of vortex shedding using fluidic actuators. PhD thesis, Virginia Tech, Blacksburg, VA.Google Scholar
Akhtar, I., Marzouk, O. A. & Nayfeh, A. H. 2009a A van der Pol–Duffing oscillator model of hydrodynamic forces on canonical structures. J. Comput. Nonlinear Dyn. 4 (4), 041006.Google Scholar
Akhtar, I., Naqvi, M., Borggaard, J. & Burns, J. A. 2013 Using dominant modes for optimal feedback control of aerodynamic forces. Proc. Inst. Mech. Engrs G 227 (12), 1859–1869.CrossRefGoogle Scholar
Akhtar, I. & Nayfeh, A. H. 2009 Model based control of vortex shedding using fluidic actuators. J. Comput. Nonlinear Dyn. 4 (4), 041006.Google Scholar
Akhtar, I., Nayfeh, A. H. & Ribbens, C. J.2008 On controlling the bluff body wake using a reduced-order model. In Proceedings of the 4th Flow Control Conference, Seattle, WA. AIAA Paper No. 2008-4189.Google Scholar
Akhtar, I., Nayfeh, A. H. & Ribbens, C. J. 2009b On the stability and extension of reduced-order Galerkin models in incompressible flows: a numerical study of vortex shedding. Theor. Comput. Fluid Dyn. 23 (3), 213–237.CrossRefGoogle Scholar
Akhtar, I., Wang, Z., Borggaard, J. & Iliescu, T. 2012 A new closure strategy for proper orthogonal decomposition reduced-order models. J. Comput. Nonlinear Dyn. 7 (3), 034503.Google Scholar
Amrouche, C. & Razafison, U. 2005 On the existence of solutions in weighted Sobolev spaces for the exterior Oseen problem. C. R. Math. 341 (9), 587–592.Google Scholar
Amrouche, C. & Rodríguez-Bellido, M. A. 2010 Very weak solutions for the stationary Oseen and Navier–Stokes equations. C. R. Math. 348 (5), 335–339.Google Scholar
Arnold, V. I. 1988 Geometric Methods in the Theory of Ordinary Differential Equations, chap. 3. Springer.Google Scholar
Atwell, J. A., Borggaard, J. T. & King, B. B. 2001 Reduced order controllers for Burgers’ equation with a nonlinear observer. Appl. Maths Comput. Sci. 11 (6), 1311–1330.Google Scholar
Atwell, J. A. & King, B. B. 1999 Computational aspects of reduced basis feedback controllers for spatially distributed systems (I). In Proceedings of the 38th IEEE Conference on Decision and Control, vol. 5, pp. 4301–4306. Citeseer.Google Scholar
Atwell, J. A. & King, B. B. 2004 Reduced order controllers for spatially distributed systems via proper orthogonal decomposition. SIAM J. Sci. Comput. 26, 128–151.Google Scholar
Bagheri, S., Henningson, D. S., Hoepffner, J. & Schmid, P. J. 2009 Input–output analysis and control design applied to a linear model of spatially developing flows. Appl. Mech. Rev. 62 (2), 020803.Google Scholar
Barbu, V., Lasiecka, I. & Triggiani, R. 2006 Tangential Boundary Stabilization of Navier–Stokes Equations. American Mathematical Society.Google Scholar
Barbu, V. & Triggiani, R. 2004 Internal stabilization of Navier–Stokes equations with finite dimensional controllers. Indiana Univ. Math. J. 7, 1443–1494.Google Scholar
Bensoussan, A., Da Prato, G., Delfour, M. C. & Mitter, S. K. 1992a Representation and Control of Infinite Dimensional Systems, Systems & Control: Foundations & Applications, vol. I. Birkhäuser.Google Scholar
Bensoussan, A., Da Prato, G., Delfour, M. C. & Mitter, S. K. 1992b Representation and Control of Infinite Dimensional Systems, Systems & Control: Foundations & Applications, vol. II. Birkhäuser.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 53, 321–575.Google Scholar
Burns, J. A. 2003 Nonlinear distributed parameter control systems with non-normal linearizations: applications and approximations. In Research Directions in Distributed Parameter Systems (ed. Smith, R. C. & Demetriou, M. A.), pp. 17–53. SIAM.Google Scholar
Burns, J. A. 2006 Modeling transition: new scenarios, system sensitivity and feedback control. In Transition and Turbulence Control (ed. Gad el Hak, M. & Tsai, H. M.), pp. 1–38. SIAM, World Scientific.Google Scholar
Burns, J. A., Ito, K. & Propst, G. 1988 On non-convergence of adjoint semigroups for control systems with delays. SIAM J. Control Optim. 26, 1442–1454.Google Scholar
Burns, J. A. & King, B. B. 1994 Optimal sensor location for robust control of distributed parameter systems. In Proceedings of the 33rd IEEE Conference on Decision and Control, pp. 3967–3972. IEEE.Google Scholar
Burns, J. A. & King, B. B. 1998 A reduced basis approach to the design of low-order feedback controllers for nonlinear continuous systems. J. Vib. Control 4 (3), 297–323.Google Scholar
Burns, J. A., King, B. B. & Rubio, D. 1998 Feedback control of a thermal fluid using state estimation. Intl J. Comput. Fluid Dyn. 11, 93–112.Google Scholar
Burns, J. A., King, B. B., Rubio, A. D. & Zietsman, L.2002 Functional gain computations for feedback control of a thermal fluid. In Proceedings of the 3rd AIAA Theoretical Fluid Mechanics Meeting. AIAA Paper 2002-2992.Google Scholar
Chen, K. K. & Rowley, C. W. 2011 H2 optimal actuator and sensor placement in the linearised complex Ginzburg–Landau system. J. Fluid Mech. 681, 241–260.Google Scholar
Chorin, A. J. 1997 A numerical method for solving incompressible viscous flow problems. J. Comput. Phys. 135 (2), 118–125.Google Scholar
Cohen, K., Siegal, S., Wetlesen, D., Cameron, J. & Sick, A. 2004 Effective sensor placements for the estimation of proper orthogonal decomposition mode coefficients in Kármán vortex street. J. Vib. Control 10, 1857–1880.Google Scholar
Deane, A. E., Kevrekidis, I. G., Karniadakis, G. E. & Orsag, S. A. 1991 Low-dimensional models for complex geometry flows: application to grooved channels and circular cylinder. Phys. Fluids A 3 (10), 2337–2354.CrossRefGoogle Scholar
Deane, A. E. & Mavriplis, C. 1994 Low-dimensional description of the dynamics in separated flow past thick airfoils. AIAA J. 6, 1222–1234.Google Scholar
Fahroo, F. & Demetriou, M. 2000 Optimal actuator/sensor location for active noise regulator and tracking control problems. J. Comput. Appl. Maths 114 (1), 137–158.Google Scholar
Farwig, R., Galdi, G. P. & Sohr, H. 2005 Very weak solutions of stationary and instationary Navier–Stokes equations with nonhomogeneous data. In Nonlinear Elliptic and Parabolic Problems, Progress in Nonlinear Differential Equations and their Applications, vol. 64, pp. 113–136. Birkhäuser.Google Scholar
Farwig, R., Galdi, G. P. & Sohr, H. 2006a A new class of weak solutions of the Navier–Stokes equations with nonhomogeneous data. J. Math. Fluid Mech. 8 (3), 423–444.Google Scholar
Farwig, R., Galdi, G. P. & Sohr, H. 2006b Very weak solutions and large uniqueness classes of stationary Navier–Stokes equations in bounded domains of $R^{2}$ . J. Differ. Equ. 227 (2), 564–580.CrossRefGoogle Scholar
Faulds, A. L. & King, B. B. 2000 Sensor location in feedback control of partial differential equation systems. In Proceedings of the 2000 IEEE International Conference on Control Applications, pp. 536–541. IEEE.Google Scholar
Fursikov, A. V. 2004 Stabilization for the 3D Navier–Stokes system by feedback boundary control. Discrete Continuous Dyn. Syst. 10 (1–2), 289–314.Google Scholar
Fursikov, A. V., Gunzburger, M. D. & Hou, L. S. 1998a Boundary value problems and optimal boundary control for the Navier–Stokes system: the two-dimensional case. SIAM J. Control Optim. 36 (3), 852–894.Google Scholar
Fursikov, A. V., Gunzburger, M. D. & Hou, L. S. 1998b Optimal Dirichlet control and inhomogeneous boundary value problems for the unsteady Navier–Stokes equations. In ESAIM: Proceedings, vol. 4, pp. 97–116. EDP Sciences.Google Scholar
Fursikov, A. V., Gunzburger, M. D. & Hou, L. S. 2005 Optimal boundary control for the evolutionary Navier–Stokes system: the three-dimensional case. SIAM J. Control Optim. 43 (6), 2191–2232.CrossRefGoogle Scholar
Gad-el-Hak, M. 1996 Modern developments in flow control. Appl. Mech. Rev. 49, 365–379.Google Scholar
Gad-el-Hak, M. 2000 Flow Control: Passive, Active, and Reactive Flow Management. Cambridge University Press.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Gillies, E. A. 1998 Low-dimensional control of the circular cylinder wake. J. Fluid Mech. 371, 157–178.CrossRefGoogle Scholar
Graham, W. R., Peraire, J. & Tang, K. Y. 1999 Optimal control of vortex shedding using low-order models. Part I – open-loop model development. Intl J. Numer. Meth. Engng 44, 945–972.Google Scholar
Gunzburger, M. D. 1995 Flow Control. Springer.Google Scholar
Hogberg, M., Bewley, T. R. & Henningson, D. S. 2003 Linear feedback control and estimation of transition in plane channel flow. J. Fluid Mech. 481, 149–175.Google Scholar
Holmes, P., Lumley, J. L. & Berkooz, G. 1996 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.Google Scholar
Illingworth, S. J., Morgans, A. S. & Rowley, C. W. 2011 Feedback control of flow resonances using balanced reduced-order models. J. Sound Vib. 330 (8), 1567–1581.CrossRefGoogle Scholar
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.Google Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes. J. Comput. Phys. 59, 308–323.Google Scholar
Leonard, B. P. 1979 A stable and accurate convective modeling procedure based on quadratic upstream interpolation. Comput. Meth. Appl. Mech. Engng 19, 59–98.Google Scholar
Lions, J.-L. 1971 Optimal Control of Systems Governed by Partial Differential Equations. Springer.Google Scholar
Luchini, P., Giannetti, F. & Pralits, J. O.2008 Structural sensitivity of linear and nonlinear global modes. AIAA paper 4227-2008.Google Scholar
Ma, X. & Karniadakis, G. 2002 A low-dimensional model for simulating three-dimensional cylinder flow. J. Fluid Mech. 458, 181–190.Google Scholar
Ma, Z., Ahuja, S. & Rowley, C. W. 2011 Reduced order models for control of fluids using the eigensystem realization algorithm. Theor. Comput. Fluid Dyn. 25 (1), 233–247.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Marzouk, O. A., Nayfeh, A. H., Akhtar, I. & Arafat, H. N. 2007 Modeling steady-state and transient forces on a cylinder. J. Vib. Control 13 (7), 1065–1091.Google Scholar
Morris, K. 2008 LQ-optimal actuator location and norm convergence of Riccati operators. In Proceedings of the 47th IEEE Conference on Decision and Control, pp. 209–214. IEEE.Google Scholar
Nayfeh, A. H., Marzouk, O. A., Haider, H. N. & Akhtar, I.2005 Modeling the transient and steady-state flow over a stationary cylinder. In ASME 20th Biennial Conference on Mechanical Vibration and Noise, 5th International Conference on Multibody Systems, Nonlinear Dynamics and Control. DETC2005-86376.Google Scholar
Noack, B. R., Afanasiev, K., Morzynski, M. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.Google Scholar
Noack, B. R., Schlegel, M., Morzynski, M. & Tadmor, G. 2010 System reduction strategy for Galerkin models of fluid flows. Intl J. Numer. Meth. Fluids 63 (2), 231–248.Google Scholar
Orszag, S. A. & Kells, L. C. 1985 Transition to turbulence in plane Poiseuille and plane Couette flow. J. Fluid Mech. 96 (1), 159–205.Google Scholar
Pastoor, M., Henning, L., Noack, B. R., King, R. & Tadmor, G. 2008 Feedback shear layer control for bluff body drag reduction. J. Fluid Mech. 608, 161–196.CrossRefGoogle Scholar
Raymond, J. P. 2007a Feedback boundary stabilization of the two-dimensional Navier–Stokes equations. SIAM J. Control Optim. 45 (3), 790–828.Google Scholar
Raymond, J. P. 2007b Feedback boundary stabilization of the three-dimensional incompressible Navier–Stokes equations. J. Math. Pures Appl. 87 (6), 627–669.Google Scholar
Raymond, J. P. & Thevenet, L. 2010 Boundary feedback stabilization of the two dimensional Navier–Stokes equations with finite dimensional controllers. Discrete Continuous Dyn. Syst. 27 (3), 1159–1187.Google Scholar
Rediniotis, O. K., Ko, J. & Kurdila, A. J. 2002 Reduced order nonlinear Navier–Stokes models for synthetic jets. Trans. ASME J. Fluids Engng 124, 433–443.CrossRefGoogle Scholar
Rediniotis, O. K., Ko, J., Yue, X. & Kurdila, A. J.1999 Synthetic jets, their reduced order modeling and applications to flow control. In 37th Aerospace Sciences Meeting & Exhibit. AIAA paper 99-1000.Google Scholar
Rowley, C. W. 2005 Model reduction for fluids, using balanced proper orthogonal decomposition. Intl J. Bifurcation Chaos 15 (3), 997–1013.Google Scholar
Siegel, S., Cohen, K. & McLaughlin, T. 2006 Numerical simulations of a feedback-controlled circular cylinder wake. AIAA J. 44 (6), 1266–1276.Google Scholar
Sipp, D., Marquet, O., Meliga, P. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open-flows: a linearized approach. Appl. Mech. Rev. 63 (3), 030801.Google Scholar
Sipp, D. & Schmid, P. J. 2013 Closed-loop control of fluid flow: a review of linear approaches and tools for the stabilization of transitional flows. AerospaceLab J. 6, 1–11.Google Scholar
Sirovich, L. & Kirby, M. 1987 Low-dimensional procedure for the characterization of human faces. J. Opt. Soc. Am. A 4 (3), 519–524.Google Scholar
Sritharan, S. S. 1991 Invariant Manifold Theory for Hydrodynamic Transition. Longman Scientific & Technical.Google Scholar
Sritharan, S. S. 1998 Optimal Control of Viscous Flow. Society for Industrial Mathematics.Google Scholar
Stoyanov, M.2009 Reduced order methods for large scale Riccati equations. PhD thesis, Virginia Tech, Blacksburg, VA.Google Scholar
Street, C. L. & Hussaini, M. Y. 1991 A numerical solution of the appearance of chaos in finite length Taylor–Couette flow. Appl. Numer. Maths 6, 123–139.Google Scholar
Tadmor, G., Lehmann, O., Noack, B. R., Cordier, L., Delville, J., Bonnet, J.-P. & Morzyński, M. 2010 Reduced order models for closed-loop wake control. Phil. Trans. R. Soc. Lond. A 369 (1940), 1513–1523.Google Scholar
Temam, R. 1997 Infinite-Dimensional Dynamical Systems in Mechanics and Physics. Springer.Google Scholar
Temam, R. 2001 Navier–Stokes Equations: Theory and Numerical Analysis. American Mathematical Society.Google Scholar
Wang, Z., Akhtar, I., Borggaard, J. & Iliescu, T. 2011 Two-level discretizations of nonlinear closure models for proper orthogonal decomposition. J. Comput. Phys. 230 (1), 126–146.Google Scholar
Wang, Z., Akhtar, I., Borggaard, J. & Iliescu, T. 2012 Proper orthogonal decomposition closure models for turbulent flows: a numerical comparison. Comput. Meth. Appl. Mech. Engng 237, 10–26.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Yildirim, B., Chryssostomidis, C. & Karniadakis, G. E. 2009 Efficient sensor placement for ocean measurements using low-dimensional concepts. Ocean Model. 27, 160–173.CrossRefGoogle Scholar
Zang, Y., Street, R. L. & Koseff, J. R. 1994 A non-staggered grid, fractional step method for time-dependent incompressible Navier–Stokes equations in curvilinear coordinates. J. Comput. Phys. 114, 18–33.CrossRefGoogle Scholar