Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T14:45:38.907Z Has data issue: false hasContentIssue false
  • English
  • Français

U-shaped fairings suppress vortex-induced vibrations for cylinders in cross-flow

Published online by Cambridge University Press:  09 October 2015

Fangfang Xie Open the ORCID record for Fangfang Xie [Opens in a new window] ,
Yue Yu ,
Yiannis Constantinides ,
Michael S. Triantafyllou  and
George Em Karniadakis
Fangfang Xie
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Yue Yu
Affiliation:
Department of Mathematics, Lehigh University, Bethlehem, PA 18015, USA
Yiannis Constantinides
Affiliation:
Chevron Energy Technology Company, Houston, TX 77002, USA
Michael S. Triantafyllou
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
George Em Karniadakis*
Affiliation:
Division of Applied Mathematics, Brown University, Providence, RI 02912, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We employ three-dimensional direct and large-eddy numerical simulations of the vibrations and flow past cylinders fitted with free-to-rotate U-shaped fairings placed in a cross-flow at Reynolds number 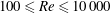$100\leqslant \mathit{Re}\leqslant 10\,000$. Such fairings are nearly neutrally buoyant devices fitted along the axis of long circular risers to suppress vortex-induced vibrations (VIVs). We consider three different geometric configurations: a homogeneous fairing, and two configurations (denoted A and AB) involving a gap between adjacent segments. For the latter two cases, we investigate the effect of the gap on the hydrodynamic force coefficients and the translational and rotational motions of the system. For all configurations, as the Reynolds number increases beyond 500, both the lift and drag coefficients decrease. Compared to a plain cylinder, a homogeneous fairing system (no gaps) can help reduce the drag force coefficient by 15 % for reduced velocity 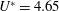$U^{\ast }=4.65$, while a type A gap system can reduce the drag force coefficient by almost 50 % for reduced velocity 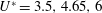$U^{\ast }=3.5,4.65,6$, and, correspondingly, the vibration response of the combined system, as well as the fairing rotation amplitude, are substantially reduced. For a homogeneous fairing, the cross-flow amplitude is reduced by about 80 %, whereas for fairings with a gap longer than half a cylinder diameter, VIVs are completely eliminated, resulting in additional reduction in the drag coefficient. We have related such VIV suppression or elimination to the features of the wake flow structure. We find that a gap causes the generation of strong streamwise vorticity in the gap region that interferes destructively with the vorticity generated by the fairings, hence disorganizing the formation of coherent spanwise cortical patterns. We provide visualization of the incoherent wake flow that leads to total elimination of the vibration and rotation of the fairing–cylinder system. Finally, we investigate the effect of the friction coefficient between cylinder and fairing. The effect overall is small, even when the friction coefficients of adjacent segments are different. In some cases the equilibrium positions of the fairings are rotated by a small angle on either side of the centreline, in a symmetry-breaking bifurcation, which depends strongly on Reynolds number.

JFM classification

Aerodynamics: Aerodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 782 , 10 November 2015 , pp. 300 - 332
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, D. W., Henning, D. L., Haws, J. H., McMillan, D. W. & McDaniel, R. B.2003 Partial helical strake for vortex-induced-vibration suppression. US Patent 6,561,734.Google Scholar
Allen, D. W., Lee, L. & Henning, D. L. 2008 Fairings versus helical strakes for suppression of vortex induced vibration: technical comparisons. In Proceedings of the Offshore Technology Conference (OTC19373), Houston, USA. Society of Petroleum Engineers.Google Scholar
Assi, G. R. S., Bearman, P. W. & Kitney, N. 2009 Low drag solutions for suppressing vortex-induced vibration of circular cylinders. J. Fluids Struct. 25 (4), 666–675.CrossRefGoogle Scholar
Baek, H. & Karniadakis, G. E. 2009 Suppressing vortex-induced vibrations via passive means. J. Fluids Struct. 25 (5), 848–866.CrossRefGoogle Scholar
Baek, H. & Karniadakis, G. E. 2011 Sub-iteration leads to accuracy and stability enhancements of semi-implicit schemes for the Navier–Stokes equations. J. Comput. Phys. 230 (12), 4384–4402.CrossRefGoogle Scholar
Baek, H. & Karniadakis, G. E. 2012 A convergence study of a new partitioned fluid–structure interaction algorithm based on fictitious mass and damping. J. Comput. Phys. 231 (2), 629–652.CrossRefGoogle Scholar
Bao, Y. & Tao, J. 2013 The passive control of wake flow behind a circular cylinder by parallel dual plates. J. Fluids Struct. 37, 201–219.CrossRefGoogle Scholar
Bearman, P. W. 1965 Investigation of the flow behind a two-dimensional model with a blunt trailing edge and fitted with splitter plates. J. Fluid Mech. 21 (2), 241–255.CrossRefGoogle Scholar
Bearman, P. W. & Branković, M. 2004 Experimental studies of passive control of vortex-induced vibration. Eur. J. Mech. (B/Fluids) 23 (1), 9–15.CrossRefGoogle Scholar
Causin, P., Gerbeau, J. F. & Nobile, F. 2005 Added-mass effect in the design of partitioned algorithms for fluid–structure problems. Comput. Meth. Appl. Mech. Engng 194 (42), 4506–4527.CrossRefGoogle Scholar
Chen, W., Xin, D., Xu, F., Li, H., Ou, J. & Hu, H. 2013 Suppression of vortex-induced vibration of a circular cylinder using suction-based flow control. J. Fluids Struct. 42, 25–39.CrossRefGoogle Scholar
Corson, D., Cosgrove, S. & Constantinides, Y. 2014 Application of CFD to predict the hydrodynamic performance of offshore fairing designs. In ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, p. V002T08A079. American Society of Mechanical Engineers.Google Scholar
Dong, S., Triantafyllou, G. S. & Karniadakis, G. E. 2008 Elimination of vortex streets in bluff-body flows. Phys. Rev. Lett. 100 (20), 204501.CrossRefGoogle ScholarPubMed
Every, M. J., King, R. & Weaver, D. S. 1982 Vortex-excited vibrations of cylinders and cables and their suppression. Ocean Engng 9 (2), 135–157.CrossRefGoogle Scholar
Galvao, R., Lee, E., Farrell, D., Hover, F., Triantafyllou, M., Kitney, N. & Beynet, P. 2008 Flow control in flow–structure interaction. J. Fluids Struct. 24 (8), 1216–1226.CrossRefGoogle Scholar
Gu, F., Wang, J. S., Qiao, X. Q. & Huang, Z. 2012 Pressure distribution, fluctuating forces and vortex shedding behavior of circular cylinder with rotatable splitter plates. J. Fluids Struct. 28, 263–278.CrossRefGoogle Scholar
Hughes, T. J. R., Liu, W. K. & Zimmermann, T. K. 1981 Lagrangian–Eulerian finite element formulation for incompressible viscous flows. Comput. Meth. Appl. Mech. Engng 29 (3), 329–349.CrossRefGoogle Scholar
Karniadakis, G. E. & Sherwin, S. 2013 Spectral/hp Element Methods for Computational Fluid Dynamics. Oxford University Press.Google Scholar
Korkischko, I. & Meneghini, J. R. 2012 Suppression of vortex-induced vibration using moving surface boundary-layer control. J. Fluids Struct. 34, 259–270.CrossRefGoogle Scholar
Kwon, K. & Choi, H. 1996 Control of laminar vortex shedding behind a circular cylinder using splitter plates. Phys. Fluids 8 (2), 479–486.CrossRefGoogle Scholar
Luo, X., Epps, B., Chryssostomidis, C. & Karniadakis, G. E. 2011 Comparison of turbulence models for simulating flow in waterjets. In Proceedings of the 11th International Conference on Fast Sea Transportation, Honolulu, HI, USA, pp. 185–191. American Society of Naval Engineers.Google Scholar
Owen, J. C., Bearman, P. W. & Szewczyk, A. A. 2001 Passive control of VIV with drag reduction. J. Fluids Struct. 15 (3), 597–605.CrossRefGoogle Scholar
Pontaza, J. P., Kotikanyadanam, M., Moeleker, P., Menon, R. G. & Bhat, S. 2012 Fairing evaluation based on numerical simulation. In ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, pp. 897–905. American Society of Mechanical Engineers.Google Scholar
Pontaza, J. P. & Menon, R. G. 2008 Numerical simulations of flow past an aspirated fairing with three degree-of-freedom motion. In ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, pp. 799–807. American Society of Mechanical Engineers.Google Scholar
Pontaza, J. P., Menon, R. G. & Chen, H. C. 2007 Three-dimensional numerical simulations of flows past smooth and rough/bare and helically straked circular cylinders allowed to undergo two degree-of-freedom motions. In ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, pp. 921–930. American Society of Mechanical Engineers.Google Scholar
Serson, D., Meneghini, J. R., Carmo, B. S., Volpe, E. V. & Gioria, R. S. 2014 Wake transition in the flow around a circular cylinder with a splitter plate. J. Fluid Mech. 755, 582–602.CrossRefGoogle Scholar
Trim, A. D., Braaten, H., Lie, H. & Tognarelli, M. A. 2005 Experimental investigation of vortex-induced vibration of long marine risers. J. Fluids Struct. 21 (3), 335–361.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2008 A brief review of recent results in vortex-induced vibrations. J. Wind Engng Ind. Aerodyn. 96 (6), 713–735.CrossRefGoogle Scholar
Yu, Y., Baek, H. & Karniadakis, G. E. 2013 Generalized fictitious methods for fluid–structure interactions: analysis and simulations. J. Comput. Phys. 245, 317–346.CrossRefGoogle Scholar
Yu, Y., Xie, F., Yan, H., Constantinides, Y., Oakley, O. & Karniadakis, G. E. 2015 Suppression of vortex-induced vibrations by fairings: a numerical study. J. Fluids Struct. 54, 679–700.CrossRefGoogle Scholar
Zdravkovich, M. M. 1981 Review and classification of various aerodynamic and hydrodynamic means for suppressing vortex shedding. J. Wind Engng Ind. Aerodyn. 7 (2), 145–189.CrossRefGoogle Scholar