Article contents
Unsteady separation leading to secondary and tertiary vortex dynamics: the sub- $\alpha $- and sub-
$\alpha $- and sub-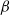 $\beta $-phenomena
$\beta $-phenomena
Published online by Cambridge University Press: 30 July 2013
Abstract
Studies on the  $\alpha $- and
$\alpha $- and 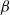 $\beta $-phenomena, terms coined by Bouard & Coutanceau (J. Fluid Mech., vol. 101, 1980, pp. 583–607) for the flow past an impulsively started circular cylinder, have been confined only to the very early stages of the flow. In this paper, besides making a comprehensive in-depth analysis of these phenomena for a much longer period of time, we report the existence of some tertiary vortex phenomena for the first time, which we term the sub-
$\beta $-phenomena, terms coined by Bouard & Coutanceau (J. Fluid Mech., vol. 101, 1980, pp. 583–607) for the flow past an impulsively started circular cylinder, have been confined only to the very early stages of the flow. In this paper, besides making a comprehensive in-depth analysis of these phenomena for a much longer period of time, we report the existence of some tertiary vortex phenomena for the first time, which we term the sub- $\alpha $- and sub-
$\alpha $- and sub-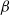 $\beta $-phenomena. The mechanism of unsteady flow separation at high Reynolds numbers for the flow past a circular cylinder developed in the last two decades has been used to understand these flow phenomena. The flow is computed using a recently developed compact finite difference method for the biharmonic form of the two-dimensional Navier–Stokes equations for the range of Reynolds number
$\beta $-phenomena. The mechanism of unsteady flow separation at high Reynolds numbers for the flow past a circular cylinder developed in the last two decades has been used to understand these flow phenomena. The flow is computed using a recently developed compact finite difference method for the biharmonic form of the two-dimensional Navier–Stokes equations for the range of Reynolds number 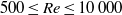 $500\leq \mathit{Re}\leq 10\hspace{0.167em} 000$. We specifically choose
$500\leq \mathit{Re}\leq 10\hspace{0.167em} 000$. We specifically choose 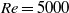 $\mathit{Re}= 5000$ to describe the interplay among the primary, secondary and tertiary vortices leading to these interesting vortex dynamics. We also report a
$\mathit{Re}= 5000$ to describe the interplay among the primary, secondary and tertiary vortices leading to these interesting vortex dynamics. We also report a 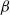 $\beta $-like phenomenon which is very similar to the
$\beta $-like phenomenon which is very similar to the 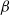 $\beta $-phenomenon, but slightly differs in details. We offer a new perception of the
$\beta $-phenomenon, but slightly differs in details. We offer a new perception of the  $\alpha $-phenomenon by defining its existence in a strong and weak sense along with a clearer characterization of the
$\alpha $-phenomenon by defining its existence in a strong and weak sense along with a clearer characterization of the 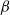 $\beta $-phenomenon. Apart from numerical computation, a detailed theoretical characterization using topological aspects of the boundary layer separation leading to the secondary and tertiary vortex phenomena has also been carried out. We compare our numerical results with established experimental and numerical results wherever available and an excellent match with the experimental results is obtained in all cases.
$\beta $-phenomenon. Apart from numerical computation, a detailed theoretical characterization using topological aspects of the boundary layer separation leading to the secondary and tertiary vortex phenomena has also been carried out. We compare our numerical results with established experimental and numerical results wherever available and an excellent match with the experimental results is obtained in all cases.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 15
- Cited by


