Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T13:37:10.775Z Has data issue: false hasContentIssue false
  • English
  • Français

The unsteady lift of an oscillating airfoil encountering a sinusoidal streamwise gust

Published online by Cambridge University Press:  08 December 2020

Ruwei Ma Open the ORCID record for Ruwei Ma [Opens in a new window] ,
Yang Yang Open the ORCID record for Yang Yang [Opens in a new window] ,
Mingshui Li Open the ORCID record for Mingshui Li [Opens in a new window]  and
Qiusheng Li Open the ORCID record for Qiusheng Li [Opens in a new window]
Ruwei Ma
Affiliation:
Research Centre for Wind Engineering, Southwest Jiaotong University, Chengdu610031, PR China
Yang Yang
Affiliation:
Research Centre for Wind Engineering, Southwest Jiaotong University, Chengdu610031, PR China Key Laboratory for Wind Engineering of Sichuan Province, Chengdu610031, PR China
Mingshui Li*
Affiliation:
Research Centre for Wind Engineering, Southwest Jiaotong University, Chengdu610031, PR China Key Laboratory for Wind Engineering of Sichuan Province, Chengdu610031, PR China
Qiusheng Li*
Affiliation:
Department of Architecture and Civil Engineering, City University of Hong Kong, Kowloon, Hong Kong
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

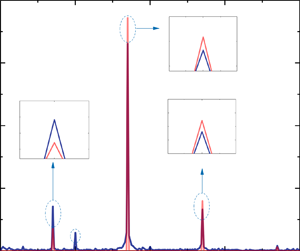
The unsteady lift of an oscillating airfoil encountering a sinusoidal streamwise gust is experimentally investigated. The sinusoidal streamwise gust is generated by a multiple-fan actively controlled wind tunnel. A two-dimensional airfoil with a NACA0015 profile oscillates in the wind tunnel with a pitch motion frequency of $f_v=1\ \textrm {Hz}$ while the sinusoidal streamwise gust has a different oscillating frequency of $f_{\beta }=1.7\ \textrm {Hz}$. The non-dimensional unsteady lift coefficients determined from surface pressure show the same trends as Greenberg's prediction. Through spectral analysis, the sum frequency $f_{sum}=f_{\beta }+f_v$ and the difference frequency $f_{diff}=|f_{\beta }-f_v|$, proposed by Greenberg, are firstly observed in the experiment. The experimental results are compared with Greenberg's theory in the case of a small amplitude of gust velocity variation $\sigma =0.2$. The results of all cases indicate that the experimental results agree generally well with Greenberg's prediction, while there is a small deviation.

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 908 , 10 February 2021 , A22
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barlas, T. K. & Van Kuik, G. A. M. 2010 Review of state of the art in smart rotor control research for wind turbines. Prog. Aerosp. Sci. 46 (1), 1–27.Google Scholar
Favier, D., Agnes, A., Barbi, C. & Maresca, C. 1988 Combined translation/pitch motion – a new airfoil dynamic stall simulation. J. Aircraft 25 (9), 805–814.CrossRefGoogle Scholar
Glegg, S. A. L. & Devenport, W. 2009 Unsteady loading on an airfoil of arbitrary thickness. J. Sound Vib. 319 (3–5), 1252–1270.CrossRefGoogle Scholar
Granlund, K., Monnier, B., Ol, M. & Williams, D. 2014 Airfoil longitudinal gust response in separated vs. attached flows. Phys. Fluids 26 (2), 1–14.Google Scholar
Greenberg, J. M. 1947 Airfoil in sinusoidal motion in a pulsating stream. NACA Tech. Rep. TN1326. National Advisory Committee for Aeronautics.Google Scholar
Halfman, R. L. 1952 Experimental aerodynamic derivatives of a sinusoidally oscillating airfoil in two-dimensional flow. NACA Tech. Rep. 1108. National Advisory Committee for Aeronautics.Google Scholar
Harding, S. F., Payne, G. S. & Bryden, I. G. 2014 Generating controllable velocity fluctuations using twin oscillating hydrofoils: experimental validation. J. Fluid Mech. 750, 113–123.CrossRefGoogle Scholar
Isaacs, R. 1945 Airfoil theory for flows of variable velocity. J. Aeronaut. Sci. 12 (1), 113–117.CrossRefGoogle Scholar
Johnson, W. 1980 Application of unsteady airfoil theory to rotary wings. J. Aircraft 17 (4), 285–286.CrossRefGoogle Scholar
von Karman, T. & Sears, W. R. 1938 Airfoil theory for nonuniform motion. J. Aeronaut. Sci. 5, 379–390.CrossRefGoogle Scholar
Kemp, N. H. & Sears, W. R. 1953 Aerodynamic interference between moving blade rows. J. Aeronaut. Sci. 20, 585–598.CrossRefGoogle Scholar
Kemp, N. H. & Sears, W. R. 1955 The unsteady forces due to viscous wakes in turbomachines. J. Aeronaut. Sci. 22, 478–483.CrossRefGoogle Scholar
Kerstens, W., Pfeiffer, J., Williams, D., King, R. & Colonius, T. 2011 Closed-loop control of lift for longitudinal gust suppression at low Reynolds numbers. AIAA J. 49 (8), 1721–1728.CrossRefGoogle Scholar
Kottapalli, S. B. R. 1985 Technical notes: unsteady aerodynamics of oscillating airfoils with inplane motions. J. Am. Helicopter Soc. 30 (1), 62–63.Google Scholar
van Kuik, G. A. M., Micallef, D., Herraez, I., van Zuijlen, A. H. & Ragni, D. 2014 The role of conservative forces in rotor aerodynamics. J. Fluid Mech. 750 (5), 284–315.Google Scholar
Leishman, J. G. 2002 Challenges in modelling the unsteady aerodynamics of wind turbines. Wind Energy 5 (2–3), 85–132.CrossRefGoogle Scholar
Monnier, B., Williams, D. R., Weier, T. & Albrecht, T. 2016 Comparison of a separated flow response to localized and global-type disturbances. Exp. Fluids 57 (7), 114.CrossRefGoogle Scholar
Motta, V., Guardone, A. & Quaranta, G. 2015 Influence of airfoil thickness on unsteady aerodynamic loads on pitching airfoils. J. Fluid Mech. 774, 460–487.Google Scholar
Rainey, A. G. 1957 Measurement of aerodynamic forces for various mean angles of attack on an airfoil oscillating in pitch and on two finite-span wings oscillating in bending with emphasis on damping in the stall. NACA Tech. Rep. 1305. National Advisory Committee for Aeronautics.Google Scholar
Reid, E. G. 1940 An experimental determination of the lift of an oscillating airfoil. J. Aero. Sci. 8 (1), 1–6.CrossRefGoogle Scholar
Sears, W. R. 1941 Some aspects of non-stationary airfoil theory and its practical application. J. Aeronaut. Sci. 8 (3), 104–108.Google Scholar
Silverstein, A. & Joyner, U. T. 1939 Experimental verification of the theory of oscillating airfoils. NACA Tech. Rep. 673. National Advisory Committee for Aeronautics.Google Scholar
Strangfeld, C., Müller-Vahl, H., Nayeri, C. N., Paschereit, C. O. & Greenblatt, D. 2016 Airfoil in a high amplitude oscillating stream. J. Fluid Mech. 793, 79–108.CrossRefGoogle Scholar
Strangfeld, C., Rumsey, C. L., Mueller-Vahl, H., Greenblatt, D., Nayeri, C. N. & Paschereit, C. O. 2015 Unsteady thick airfoil aerodynamics: experiments, computation, and theory. In AIAA Paper 2015-3071, 45th AIAA Fluid Dynamics Conference. American Institute of Aeronautics and Astronautics.Google Scholar
Szumowski, A. P. & Meier, G. E. A. 1996 Forced oscillations of airfoil flows. Exp. Fluids 21 (6), 457–464.CrossRefGoogle Scholar
Theodorsen, T. 1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. 496, pp. 413–433. National Advisory Committee for Aeronautics.Google Scholar
van der Wall, B. G. & Leishman, J. G. 1994 On the influence of time-varying flow velocity on unsteady aerodynamics. J. Am. Helicopter Soc. 39 (4), 25.CrossRefGoogle Scholar
Yang, Y., Li, M., Ma, C. & Li, S. 2017 Experimental investigation on the unsteady lift of an airfoil in a sinusoidal streamwise gust. Phys. Fluids 29 (5), 051703.CrossRefGoogle Scholar