Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T14:02:51.678Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsteadiness in a large turbulent separation bubble

Published online by Cambridge University Press:  23 June 2016

Abdelouahab Mohammed-Taifour  and
Julien Weiss
Abdelouahab Mohammed-Taifour
Affiliation:
Laboratoire de thermo-fluide pour le transport, École de technologie supérieure, Montréal, Québec H3C 1K3, Canada
Julien Weiss*
Affiliation:
Laboratoire de thermo-fluide pour le transport, École de technologie supérieure, Montréal, Québec H3C 1K3, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The unsteady behaviour of a massively separated, pressure-induced turbulent separation bubble (TSB) is investigated experimentally using high-speed particle image velocimetry (PIV) and piezo-resistive pressure sensors. The TSB is generated on a flat test surface by a combination of adverse and favourable pressure gradients. 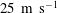The Reynolds number based on the momentum thickness of the incoming boundary layer is 5000 and the free stream velocity is $25~\text{m}~\text{s}^{-1}$. The proper orthogonal decomposition (POD) is used to separate the different unsteady modes in the flow. The first POD mode contains approximately 30 % of the total kinetic energy and is shown to describe a low-frequency contraction and expansion, called ‘breathing’, of the TSB. This breathing is responsible for a variation in TSB size of approximately 90 % of its average length. It also generates low-frequency wall-pressure fluctuations that are mainly felt upstream of the mean detachment and downstream of the mean reattachment. A medium-frequency unsteadiness, which is linked to the convection of large-scale vortices in the shear layer bounding the recirculation zone and their shedding downstream of the TSB, is also observed. When scaled with the vorticity thickness of the shear layer and the convection velocity of the structures, this medium frequency is very close to the characteristic frequency of vortices convected in turbulent mixing layers. The streamwise position of maximum vertical turbulence intensity generated by the convected structures is located downstream of the mean reattachment line and corresponds to the position of maximum wall-pressure fluctuations.

JFM classification

Boundary Layers: Boundary layer separation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 799 , 25 July 2016 , pp. 383 - 412
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Adrian, R. J. & Westerweel, J. 2010 Particle Image Velocimetry, Cambridge Aerospace Series. Cambridge University Press.Google Scholar
Alving, A. E. & Fernholz, H. H. 1996 Turbulence measurements around a mild separation bubble and downstream of reattachment. J. Fluid Mech. 322, 297–328.Google Scholar
Angele, K. P. & Muhammad-Klingmann, B. 2006 PIV measurements in a weakly separating and reattaching turbulent boundary layer. Eur. J. Mech. (B/Fluids) 25 (2), 204–222.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.Google Scholar
de Brederode, V. & Bradshaw, P.1972 Three-dimensional flow in nominally two-dimensional separation bubbles: I. Flow behind a rearward-facing step. Tech. Rep. 72-19. Imperial College of Science and Technology.Google Scholar
Browand, F. K. & Troutt, T. R. 1985 The turbulent mixing layer: geometry of large vortices. J. Fluid Mech. 158, 489–509.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (04), 775–816.CrossRefGoogle Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.Google Scholar
Chen, H., Reuss, D. L., Hung, D. L. S. & Sick, V. 2012 A practical guide for using proper orthogonal decomposition in engine research. Intl J. Engine Res. 14 (4), 307–319.Google Scholar
Cheng, W., Pullin, D. I. & Samtaney, R. 2015 Large-eddy simulation of separation and reattachment of a flat plate turbulent boundary layer. J. Fluid Mech. 785, 78–108.CrossRefGoogle Scholar
Cherry, N. J., Hillier, R. & Latour, M. E. M. P. 1984 Unsteady measurements in a separated and reattaching flow. J. Fluid Mech. 144, 13–46.Google Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.Google Scholar
De Graaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Dengel, P. & Fernholz, H. H. 1990 An experimental investigation of an incompressible turbulent boundary layer in the vicinity of separation. J. Fluid Mech. 212, 615–636.Google Scholar
Dianat, M. & Castro, I. P. 1991 Turbulence in a separated boundary layer. J. Fluid Mech. 226, 91–123.CrossRefGoogle Scholar
Duquesne, P., Maciel, Y. & Deschênes, C. 2015 Unsteady flow separation in a turbine diffuser. Exp. Fluids 56 (8), 1–15.Google Scholar
Dussauge, J.-P., Dupont, P. & Debiève, J.-F. 2006 Unsteadiness in shock wave boundary layer interactions with separation. Aerosp. Sci. Technol. 10 (2), 85–91.CrossRefGoogle Scholar
Eaton, J. K. & Johnston, J. P. 1982 Low frequency unsteadiness of a reattaching turbulent shear layer. In Turbulent Shear Flows 3, vol. 2, pp. 162–170.Google Scholar
Foss, J. 2004 Surface selections and topological constraint evaluations for flow field analyses. Exp. Fluids 37 (6), 883–898.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2009 Low-frequency dynamics of shock-induced separation in a compression ramp interaction. J. Fluid Mech. 636, 397–425.Google Scholar
Graftieaux, L., Michard, M. & Grosjean, N. 2001 Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 12 (9), 1422–1429.Google Scholar
Hudy, L. M., Naguib, A. M. & Humphreys, W. M. 2003 Wall-pressure-array measurements beneath a separating/reattaching flow region. Phys. Fluids 15 (3), 706–717.Google Scholar
Hudy, L. M., Naguib, A. M. & Humphreys, W. M. 2007 Stochastic estimation of a separated-flow field using wall-pressure-array measurements. Phys. Fluids 19, 024103.Google Scholar
Humble, R. A., Scarano, F. & Van Oudheusden, B. W. 2009 Unsteady aspects of an incident shock wave/turbulent boundary layer interaction. J. Fluid Mech. 635, 47–74.Google Scholar
Hunt, J. C. R., Abell, C. J., Peterka, J. A. & Woo, H. 1978 Kinematical studies of the flows around free or surface-mounted obstacles; applying topology to flow visualization. J. Fluid Mech. 86 (01), 179–200.Google Scholar
Hunt, J. C. R., Wray, A. & Moin, P.1988 Eddies, stream, and convergence zones in turbulent flows. Report CTR-S88, pp. 193–208. Center for Turbulence Research.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Ji, M. & Wang, M. 2012 Surface pressure fluctuations on steps immersed in turbulent boundary layers. J. Fluid Mech. 712, 471–504.CrossRefGoogle Scholar
Kaltenbach, H.-J., Fatica, M., Mittal, R., Lund, T. S. & Moin, P. 1999 Study of flow in a planar asymmetric diffuser using large-eddy simulation. J. Fluid Mech. 390, 151–185.CrossRefGoogle Scholar
Kiya, M. & Sasaki, K. 1983 Structure of a turbulent separation bubble. J. Fluid Mech. 137, 83–113.Google Scholar
Mabey, D. G. 1972 Analysis and correlation of data on pressure fluctuations in separated flows. J. Aircraft 9 (9), 642–645.Google Scholar
Malm, J., Schlatter, P. & Henningson, D. S. 2012 Coherent structures and dominant frequencies in a turbulent three-dimensional diffuser. J. Fluid Mech. 699, 320–351.Google Scholar
Mohammed-Taifour, A., Schwaab, Q., Pioton, J. & Weiss, J. 2015a A new wind tunnel for the study of pressure-induced separating and reattaching flows. Aeronaut. J. 119 (1211), 91–108.Google Scholar
Mohammed-Taifour, A., Weiss, J., Sadeghi, A., Vétel, J., Jondeau, E. & Comte-Bellot, G. 2015b A detailed procedure for measuring turbulent velocity fluctuations using constant-voltage anemometry. Exp. Fluids 56 (9), 1–13.Google Scholar
Na, Y. & Moin, P. 1998a Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 374, 379–405.Google Scholar
Na, Y. & Moin, P. 1998b The structure of wall-pressure fluctuations in turbulent boundary layers with adverse pressure gradient and separation. J. Fluid Mech. 377, 347–373.Google Scholar
Naguib, A. M., Gravante, S. P. & Wark, C. E. 1996 Extraction of turbulent wall-pressure time-series using an optimal filtering scheme. Exp. Fluids 22, 14–22.CrossRefGoogle Scholar
Patrick, W. P.1987 Flowfield measurements in a separated and reattached flat plate turbulent boundary layer. NASA Tech. Rep. 4052.Google Scholar
Pearson, D. S., Goulart, P. J. & Ganapathisubramani, B. 2013 Turbulent separation upstream of a forward-facing step. J. Fluid Mech. 724, 284–304.CrossRefGoogle Scholar
Perry, A. E. & Fairlie, B. D. 1975 A study of turbulent boundary-layer separation and reattachment. J. Fluid Mech. 69 (4), 657–672.Google Scholar
Piponniau, S., Dussauge, J.-P., Debiève, J. F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.Google Scholar
Ruderich, R. & Fernholz, H. H. 1986 An experimental investigation of a turbulent shear flow with separation, reverse flow, and reattachment. J. Fluid Mech. 163, 283–322.Google Scholar
Sartor, F., Mettot, C., Bur, R. & Sipp, D. 2015 Unsteadiness in transonic shock-wave/boundary-layer interactions: experimental investigation and global stability analysis. J. Fluid Mech. 781, 550–577.Google Scholar
Scarano, F. & Riethmuller, M. L. 1999 Iterative multigrid approach in PIV image processing with discrete window offset. Exp. Fluids 26 (6), 513–523.Google Scholar
Schwaab, Q. & Weiss, J. 2015 Evaluation of a thermal-tuft probe for turbulent separating and reattaching flows. Trans. ASME J. Fluids Engng 137, 011401.Google Scholar
Simpson, R. L. 1989 Turbulent boundary-layer separation. Annu. Rev. Fluid Mech. 21, 205–234.CrossRefGoogle Scholar
Simpson, R. L. 1996 Aspects of turbulent boundary-layer separation. Prog. Aerosp. Sci. 32, 457–521.Google Scholar
Sipp, D., Marquet, O., Meliga, P. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open-flows: a linearized approach. Appl. Mech. Rev. 63 (3), 030801.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part I: coherent structures. Q. Appl. Maths 45 (3), 561–571.Google Scholar
Skote, M. & Henningson, D. S. 2002 Direct numerical simulation of a separated turbulent boundary layer. J. Fluid Mech. 471, 107–136.Google Scholar
Spalart, P. R. & Coleman, G. N. 1997 Numerical study of a separation bubble with heat transfer. Eur. J. Mech. (B/Fluids) 16 (2), 169–189.Google Scholar
Surana, A., Grunberg, O. & Haller, G. 2006 Exact theory of three-dimensional flow separation. Part 1. Steady separation. J. Fluid Mech. 564, 57–103.Google Scholar
Thacker, A., Aubrun, S., Leroy, A. & Devinant, P. 2013 Experimental characterization of flow unsteadiness in the centerline plane of an Ahmed body rear slant. Exp. Fluids 54 (3), 1–16.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.Google Scholar
Troutt, T. R., Scheelke, B. & Norman, T. R. 1984 Organized structures in a reattaching separated flow field. J. Fluid Mech. 143, 413–427.CrossRefGoogle Scholar
Trünkle, J., Mohammed-Taifour, A. & Weiss, J. 2016 Fluctuating pressure measurements in a turbulent separation bubble. C. R. Méc. 344 (1), 60–67.Google Scholar
Weiss, J., Mohammed-Taifour, A. & Schwaab, Q. 2015 Unsteady behavior of a pressure-induced turbulent separation bubble. AIAA J. 53 (9), 2634–2645.Google Scholar
Winant, C. D. & Browand, F. K. 1974 Vortex pairing: the mechanism of turbulent mixing-layer growth at moderate reynolds number. J. Fluid Mech. 63 (02), 237–255.CrossRefGoogle Scholar