Article contents
A universal three-dimensional instability of the wakes of two-dimensional bluff bodies
Published online by Cambridge University Press: 29 February 2016
Abstract
Linear stability analysis of a wide range of two-dimensional and axisymmetric bluff-body wakes shows that the first three-dimensional mode to became unstable is always mode E. From the studies presented in this paper, it is speculated to be the universal primary 3D instability, irrespective of the flow configuration. However, since it is a transition from a steady two-dimensional flow, whether this mode can be observed in practice does depend on the nature of the flow set-up. For example, the mode E transition of a circular cylinder wake occurs at a Reynolds number of 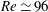 $\mathit{Re}\simeq 96$, which is considerably higher than the steady to unsteady Hopf bifurcation at
$\mathit{Re}\simeq 96$, which is considerably higher than the steady to unsteady Hopf bifurcation at 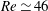 $\mathit{Re}\simeq 46$ leading to Bénard–von-Kármán shedding. On the other hand, if the absolute instability responsible for the latter transition is suppressed, by rotating the cylinder or moving it towards a wall, then mode E may become the first transition of the steady flow. A well-known example is flow over a backward-facing step, where this instability is the first global instability to be manifested on the otherwise two-dimensional steady flow. Many other examples are considered in this paper. Exploring this further, a structural stability analysis (Pralits et al.J. Fluid Mech., vol. 730, 2013, pp. 5–18) was conducted for the subset of flows past a rotating cylinder as the rotation rate was varied. For the non-rotating or slowly rotating case, this indicated that the growth rate of the instability mode was sensitive to forcing between the recirculation lobes, while for the rapidly rotating case, it confirmed sensitivity near the cylinder and towards the hyperbolic point. For the non-rotating case, the perturbation, adjoint and structural stability fields, together with the wavelength selection, show some similarities with those of a Crow instability of a counter-rotating vortex pair, at least within the recirculation zones. On the other hand, at much higher rotation rates, Pralits et al. (J. Fluid Mech., vol. 730, 2013, pp. 5–18) have suggested that hyperbolic instability may play a role. However, both instabilities lie on the same continuous solution branch in Reynolds number/rotation-rate parameter space. The results suggest that this particular flow transition at least, and probably others, may have a number of different physical mechanisms supporting their development.
$\mathit{Re}\simeq 46$ leading to Bénard–von-Kármán shedding. On the other hand, if the absolute instability responsible for the latter transition is suppressed, by rotating the cylinder or moving it towards a wall, then mode E may become the first transition of the steady flow. A well-known example is flow over a backward-facing step, where this instability is the first global instability to be manifested on the otherwise two-dimensional steady flow. Many other examples are considered in this paper. Exploring this further, a structural stability analysis (Pralits et al.J. Fluid Mech., vol. 730, 2013, pp. 5–18) was conducted for the subset of flows past a rotating cylinder as the rotation rate was varied. For the non-rotating or slowly rotating case, this indicated that the growth rate of the instability mode was sensitive to forcing between the recirculation lobes, while for the rapidly rotating case, it confirmed sensitivity near the cylinder and towards the hyperbolic point. For the non-rotating case, the perturbation, adjoint and structural stability fields, together with the wavelength selection, show some similarities with those of a Crow instability of a counter-rotating vortex pair, at least within the recirculation zones. On the other hand, at much higher rotation rates, Pralits et al. (J. Fluid Mech., vol. 730, 2013, pp. 5–18) have suggested that hyperbolic instability may play a role. However, both instabilities lie on the same continuous solution branch in Reynolds number/rotation-rate parameter space. The results suggest that this particular flow transition at least, and probably others, may have a number of different physical mechanisms supporting their development.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 6
- Cited by



