Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T21:49:02.806Z Has data issue: false hasContentIssue false
  • English
  • Français

A universal scaling for low-order structure functions in the log-law region of smooth- and rough-wall boundary layers

Published online by Cambridge University Press:  02 July 2014

P. A. Davidson  and
P.-Å. Krogstad
P. A. Davidson
Affiliation:
Department of Engineering, Cambridge University, Trumpington Street, Cambridge CB2 1PZ, UK
P.-Å. Krogstad*
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, 7491 Trondheim, Norway
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

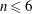We consider the log-law layer of both smooth- and rough-wall boundary layers at large Reynolds number. A scaling theory is proposed for low-order structure functions (say $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}n \leq 6$) in the range of scales 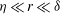$\eta \ll r \ll \delta $, where 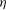$\eta $ is the Kolmogorov length and $\delta $ is the boundary layer thickness. This theory rests on the hypothesis that the turbulence in this intermediate range of scales depends only on the scale $r$, the local dissipation rate and the shear velocity. Crucially, the structure of the turbulence is assumed to be independent of the distance from the wall, 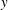$y$, except to the extent that 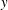$y$ sets the value of the local dissipation rate. A detailed comparison is made between the predictions of the theory and data taken from both smooth- and rough-wall boundary layers. The data support the hypothesis that it is the dissipation rate, and not 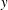$y$, that controls the structure of the turbulence for this range of eddy sizes. Our findings provide the first unified scaling theory for both smooth- and rough-wall turbulence.

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 140 - 156
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. A. & Krogstad, P.-Å. 2001 Turbulence structure in boundary layers over different types of surface roughness. Fluid Dyn. Res. 28, 139–157.Google Scholar
Arad, I., Biferale, L., Mazzitelli, I. & Procaccia, I. 1999 Disentangling scaling properties in anisotropic and inhomogeneous turbulence. Phys. Rev. Lett. 82 (25), 5040–5043.Google Scholar
Benzi, R., Amati, G., Casciola, C. M., Toschi, F. & Piva, R. 1999 Intermittency and scaling laws for wall bounded turbulence. Phys. Fluids 11 (6), 1284–1286.Google Scholar
Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and turbulent transport. Phys. Rep. 414, 43–164.Google Scholar
Casciola, C. M., Benzi, R., Gualtieri, P., Jacobs, B. & Piva, R. 2001 Double scaling and intermittency in shear dominated flows. Phys. Rev. E 65, 015301.Google Scholar
Casciola, C. M., Gualtieri, P., Benzi, R. & Piva, R. 2003 Scale-by-scale budget and similarity laws for shear turbulence. J. Fluid Mech. 476, 105–114.Google Scholar
Casciola, C. M., Gualtieri, P., Jacobs, B. & Piva, R. 2005 Scaling properties in the production range of shear dominated flows. Phys. Rev. Lett. 95, 024503.CrossRefGoogle ScholarPubMed
Davidson, P. A. 2004 Turbulence, An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Davidson, P. A. & Krogstad, P.-Å. 2009 A simple model for the streamwise fluctuations in the log-law region of a boundary layer. Phys. Fluids 21, 055105.Google Scholar
Davidson, P. A., Krogstad, P.-Å. & Nickels, T. 2006a A refined interpretation of the logarithmic structure function law in wall layer turbulence. Phys. Fluids 18, 065112.Google Scholar
Davidson, P. A., Nickels, T. & Krogstad, P.-Å. 2006b The logarithmic structure function law in wall-layer turbulence. J. Fluid Mech. 550, 51–60.Google Scholar
van Driest, E. R. 1956 On turbulent flow near a wall. J. Aeronaut. Sci. 23, 1007–1011.Google Scholar
Gualtieri, P., Casciola, C. M., Benzi, R., Amati, G. & Piva, R. 2002 Scaling laws and intermittency in homogeneous shear flow. Phys. Fluids 14 (2), 583–596.Google Scholar
Krogstad, P.-Å., Antonia, R. A. A. & Browne, L. W. B. 1992 Comparison between rough- and smooth-wall boundary layers. J. Fluid Mech. 245, 599–617.CrossRefGoogle Scholar
Krogstad, P.-Å. & Efros, V. 2012 About turbulence statistics in the outer part of a boundary layer developing over two-dimensional surface roughness. Phys. Fluids 24, 075112.Google Scholar
Poggi, D., Porporato, A. & Ridolfi, L. 2003 Analysis of the small-scale structure of turbulence on smooth and rough walls. Phys. Fluids 15 (1), 35–46.Google Scholar
Ruiz-Chavarria, G., Ciliberto, S., Baudet, C. & Leveque, E. 2000 Scaling properties of the streamwise component of velocity in a turbulent boundary layer. Physica D 141, 183–198.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Toschi, F., Amati, G., Succi, S., Benzi, R. & Piva, R. 1999 Intermittency and structure functions in channel flow turbulence. Phys. Rev. Lett. 82 (25), 5044–5047.CrossRefGoogle Scholar
Toschi, F., Leveque, E. & Ruiz-Chavarria, G. 2000 Shear effects in nonhomogeneous turbulence. Phys. Rev. Lett. 85 (7), 1436–1439.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flows, 2nd edn. Cambridge University Press.Google Scholar