Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T02:41:19.675Z Has data issue: false hasContentIssue false
  • English
  • Français

The universal aspect ratio of vortices in rotating stratified flows: theory and simulation

Published online by Cambridge University Press:  25 May 2012

Pedram Hassanzadeh ,
Philip S. Marcus  and
Patrice Le Gal
Pedram Hassanzadeh
Affiliation:
Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA
Philip S. Marcus*
Affiliation:
Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA
Patrice Le Gal
Affiliation:
Institut de Recherche sur les Phénomènes Hors Equilibre, UMR 7342, CNRS - Aix-Marseille Université, 49 rue F. Joliot Curie, 13384 Marseille, CEDEX 13, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive a relationship for the vortex aspect ratio (vertical half-thickness over horizontal length scale) for steady and slowly evolving vortices in rotating stratified fluids, as a function of the Brunt–Väisälä frequencies within the vortex 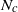and in the background fluid outside the vortex 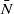, the Coriolis parameter 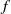and the Rossby number 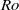of the vortex: 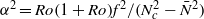. This relation is valid for cyclones and anticyclones in either the cyclostrophic or geostrophic regimes; it works with vortices in Boussinesq fluids or ideal gases, and the background density gradient need not be uniform. Our relation for has many consequences for equilibrium vortices in rotating stratified flows. For example, cyclones must have 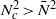; weak anticyclones (with 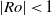) must have 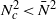; and strong anticyclones must have 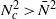. We verify our relation for with numerical simulations of the three-dimensional Boussinesq equations for a wide variety of vortices, including: vortices that are initially in (dissipationless) equilibrium and then evolve due to an imposed weak viscous dissipation or density radiation; anticyclones created by the geostrophic adjustment of a patch of locally mixed density; cyclones created by fluid suction from a small localized region; vortices created from the remnants of the violent breakups of columnar vortices; and weakly non-axisymmetric vortices. The values of the aspect ratios of our numerically computed vortices validate our relationship for , and generally they differ significantly from the values obtained from the much-cited conjecture that 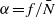in quasi-geostrophic vortices.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 46 - 57
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Armi, L., Hebert, D., Oakey, N., Price, J. F., Richardson, P. L., Rossby, H. T. & Ruddick, B. 1988 The history and decay of a Mediterranean salt lens. Nature 333 (6174), 649–651.CrossRefGoogle Scholar
2. Aubert, O., Le Bars, M., Le Gal, P. & Marcus, P. S. 2012 The universal aspect ratio of vortices in rotating stratified flows: experiments and Observations. J. Fluid Mech. 706, 34–45.CrossRefGoogle Scholar
3. Barcilon, V. & Pedlosky, J. 1967 On the steady motions produced by a stable stratification in a rapidly rotating fluid. J. Fluid Mech. 29, 673–690.CrossRefGoogle Scholar
4. Barranco, J. A. & Marcus, P. S. 2005 Three-dimensional vortices in stratified protoplanetary disks. Astrophys. J. 623 (2), 1157–1170.CrossRefGoogle Scholar
5. Barranco, J. A. & Marcus, P. S. 2006 A 3D spectral anelastic hydrodynamic code for shearing, stratified flows. J. Comput. Phys. 219 (1), 21–46.CrossRefGoogle Scholar
6. Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13 (6), 1645–1651.CrossRefGoogle Scholar
7. Carton, X. 2001 Hydrodynamical modeling of oceanic vortices. Surv. Geophys. 22 (3), 79–263.CrossRefGoogle Scholar
8. Charney, J. G. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1095.2.0.CO;2>CrossRefGoogle Scholar
9. Dritschel, D. G., Juarez, M. D. & Ambaum, M. H. P. 1999 The three-dimensional vortical nature of atmospheric and oceanic turbulent flows. Phys. Fluids 11 (6), 1512–1520.CrossRefGoogle Scholar
10. Gent, P. R. & McWilliams, J. C. 1986 The instability of barotropic circular vortices. Geophys. Astrophys. Fluid Dyn. 35, 209–233.CrossRefGoogle Scholar
11. Gill, A. E. 1981 Homogeneous intrusions in a rotating stratified fluid. J. Fluid Mech. 103, 275–295.CrossRefGoogle Scholar
12. Humphreys, T. & Marcus, P. S. 2007 Vortex street dynamics: the selection mechanism for the areas and locations of Jupiter’s vortices. J. Atmos. Sci. 64 (4), 1318–1333.CrossRefGoogle Scholar
13. Marcus, P. S. 1993 Jupiter’s Great Red Spot and other vortices. Annu. Rev. Astron. Astrophys. 31, 523–573.CrossRefGoogle Scholar
14. McWilliams, J. C. 1985 Submesoscale, coherent vortices in the ocean. Rev. Geophys. 23 (2), 165–182.CrossRefGoogle Scholar
15. McWilliams, J. C. 1988 Vortex generation through balanced adjustment. J. Phys. Oceanogr. 18 (8), 1178–1192.2.0.CO;2>CrossRefGoogle Scholar
16. McWilliams, J. C., Weiss, J. B. & Yavneh, I. 1994 Anisotropy and coherent vortex structures in planetary turbulence. Science 264 (5157), 410–413.CrossRefGoogle ScholarPubMed
17. McWilliams, J. C., Weiss, J. B. & Yavneh, I. 1999 The vortices of homogeneous geostrophic turbulence. J. Fluid Mech. 401, 1–26.CrossRefGoogle Scholar
18. Morel, Y. & McWilliams, J. 1997 Evolution of isolated interior vortices in the ocean. J. Phys. Oceanogr. 27 (5), 727–748.2.0.CO;2>CrossRefGoogle Scholar
19. Nof, D. 1981 On the -induced movement of isolated baroclinic eddies. J. Phys. Oceanogr. 11 (12), 1662–1672.2.0.CO;2>CrossRefGoogle Scholar
20. de Pater, I., Wong, M. H., Marcus, P., Luszcz-Cook, S., Adamkovics, M., Conrad, A., Asay-Davis, X. & Go, C. 2010 Persistent rings in and around Jupiter’s anticyclones – observations and theory. Icarus 210 (2), 742–762.CrossRefGoogle Scholar
21. Reinaud, J. N., Dritschel, D. G. & Koudella, C. R. 2003 The shape of vortices in quasi-geostrophic turbulence. J. Fluid Mech. 474, 175–192.CrossRefGoogle Scholar
22. Sayanagi, K. M., Morales-Juberias, P. & Ingersoll, A. P. 2010 Saturn’s Northern Hemisphere Ribbon: simulations and comparison with the meandering Gulf Stream. J. Atmos. Sci. 67 (8), 2658–2678.CrossRefGoogle Scholar
23. Shetty, S. & Marcus, P. S. 2010 Changes in Jupiter’s Great Red Spot (1979–2006) and Oval BA (2000–2006). Icarus 210 (1), 182–2018.CrossRefGoogle Scholar
24. Smyth, W. D. & McWilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. Theor. Comput. Fluid Dyn. 11 (3–4), 305–322.CrossRefGoogle Scholar
25. Stuart, G. A., Sundermeyer, M. A. & Hebert, D. 2011 On the geostrophic adjustment of an isolated lens: dependence on burger number and initial geometry. J. Phys. Oceanogr. 41 (4), 725–741.CrossRefGoogle Scholar
26. Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
27. Van Heijst, G. J. F. & Kloosterziel, R. C. 1989 Tripolar vortices in a rotating fluid. Nature 338 (6216), 569–571.CrossRefGoogle Scholar